MATLAB 绘制 SISO 和 MIMO 线性系统的时间和频率响应图
系列文章目录
文章目录
- 系列文章目录
- 前言
- 一、时间响应
- 二、频率响应
- 三、极点/零点图和根节点
- 四、响应特性
- 五、分析 MIMO 系统
- 六、系统比较
- 七、修改时间轴或频率轴数值
- `如果觉得内容不错,请点赞、收藏、关注`
前言
本例演示如何绘制 SISO 和 MIMO 线性系统的时间和频率响应图。
一、时间响应
创建线性系统。在本例中,创建一个三阶传递函数。
sys = tf([8 18 32],[1 6 14 24])
sys =
8 s^2 + 18 s + 32
-----------------------
s^3 + 6 s^2 + 14 s + 24
连续时间传递函数。
模型属性
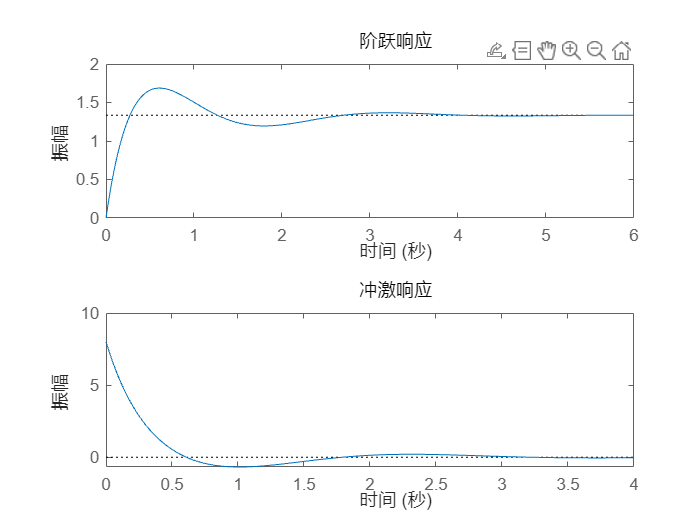
您可以使用 step and impulse 命令绘制该系统的阶跃和脉冲响应。
subplot(2,1,1)
step(sys)
subplot(2,1,2)
impulse(sys)
您还可以使用 lsim 命令模拟对正弦波等任意信号的响应。输入信号显示为灰色,系统响应显示为蓝色。
clf
t = 0:0.01:4;
u = sin(10*t);
lsim(sys,u,t) % u,t define the input signal
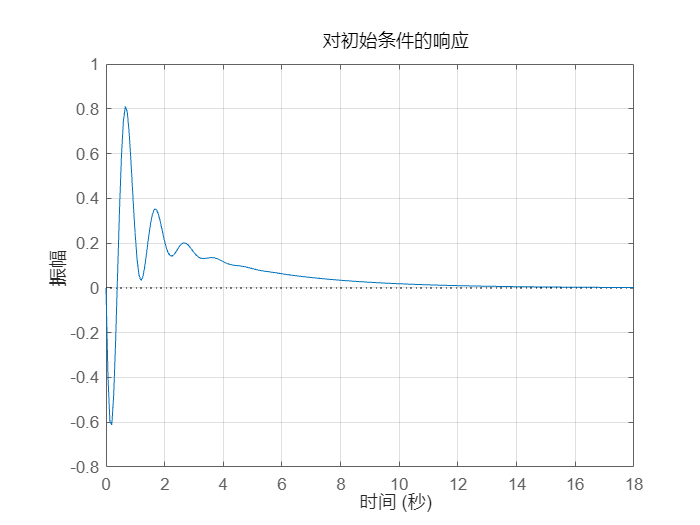
您可以在连续或离散的 tf、ss 或 zpk 模型中使用绘图命令。对于状态空间模型,您还可以绘制从给定初始状态开始的非强迫响应。例如
A = [-0.8 3.6 -2.1;-3 -1.2 4.8;3 -4.3 -1.1];
B = [0; -1.1; -0.2];
C = [1.2 0 0.6];
D = -0.6;
G = ss(A,B,C,D);
x0 = [-1;0;2]; % initial state
initial(G,x0)
grid
二、频率响应
频域分析是了解控制系统稳定性和性能特性的关键。Bode 图、Nyquist 图和 Nichols 图是绘制和分析线性系统频率响应的三种标准方法。您可以使用 Bode、Nichols 和 Nyquist 命令创建这些图。
创建线性系统。
sys = tf([8 18 32],[1 6 14 24])
sys =
8 s^2 + 18 s + 32
-----------------------
s^3 + 6 s^2 + 14 s + 24
连续时间传递函数。
模型属性
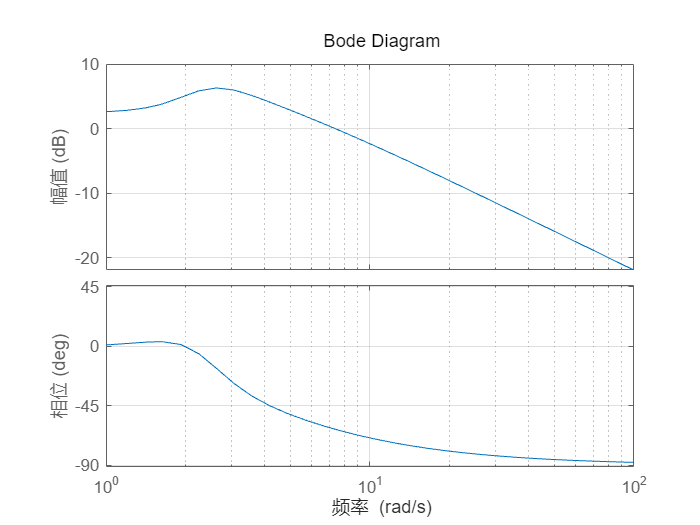
为该系统绘制 Bode 图。
bode(sys)
grid
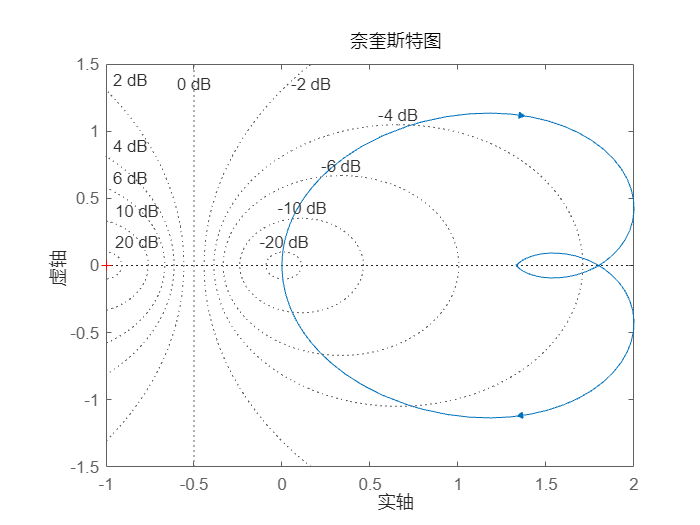
为该系统绘制奈奎斯特图。
nyquist(sys)
grid
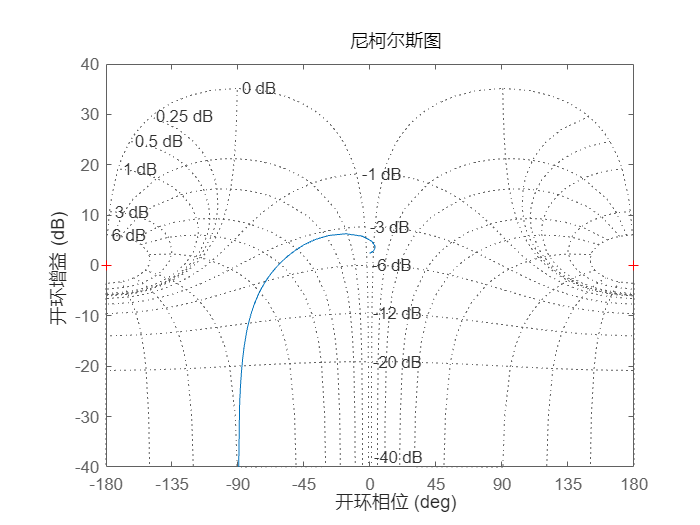
为该系统创建一个尼科尔斯图表。
nichols(sys)
grid
三、极点/零点图和根节点
系统的极点和零点包含有关其动态、稳定性和性能极限的宝贵信息。例如,考虑以下 SISO 控制回路中的反馈回路。
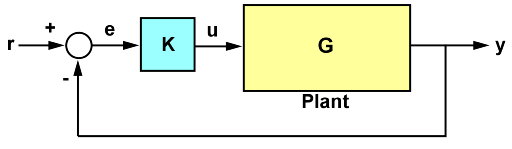
G = − ( 2 s + 1 ) s 2 + 3 s + 2 G=\frac{-(2s+1)}{s^{2}+3s+2} G=s2+3s+2−(2s+1)
对于增益值 k = 0.7,可以使用 pzmap 绘制闭环极点和零点图。
s = tf('s');
G = -(2*s+1)/(s^2+3*s+2);
k = 0.7;
T = feedback(G*k,1);
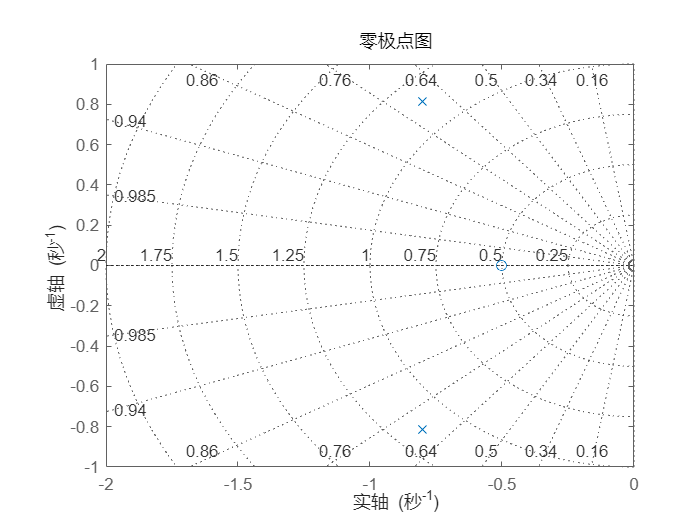
pzmap(T)
grid, axis([-2 0 -1 1])
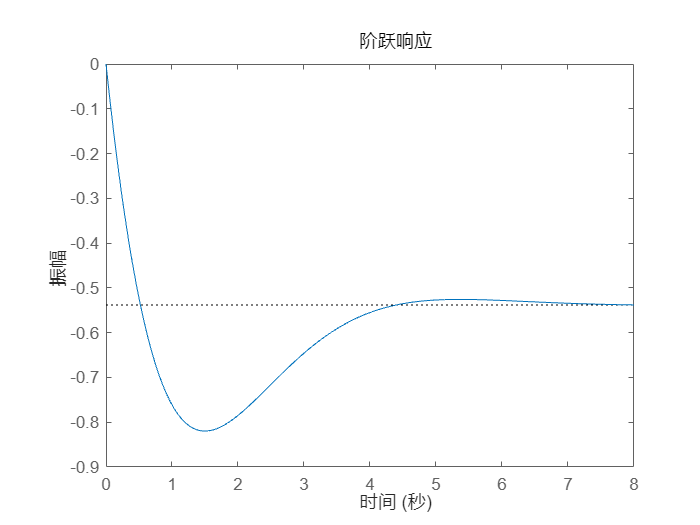
闭环极点(蓝色 x 标记)位于左半平面内,因此在选择增益 k 时,反馈回路是稳定的。这里的阻尼比约为 0.7,表明闭环响应阻尼良好,这一点可以通过以下数据得到证实:
clf
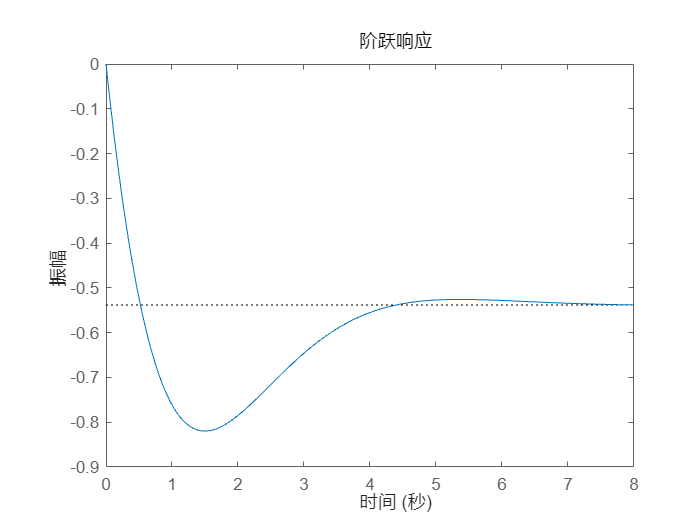
step(T)
为了进一步了解环路增益 k 对闭环稳定性的影响,可以绘制闭环极点位置与 k 的函数关系图。
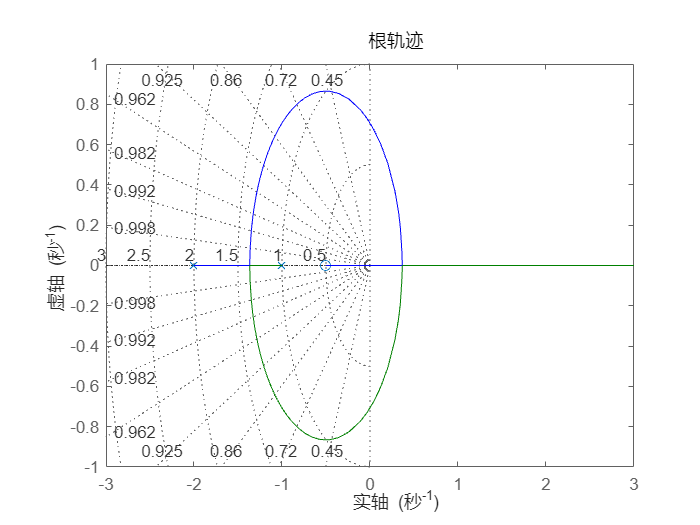
rlocus(G)
grid
点击定位点与 y 轴相交的位置,可以发现当 k = 1.51 时,闭环极点变得不稳定。因此,为保证闭环稳定,环路增益应保持小于 1.5。
四、响应特性
右键单击响应图可以访问各种选项和注释。特别是,通过特性菜单可以显示标准指标,如阶跃响应的上升时间和稳定时间,或频率响应图的峰值增益和稳定裕度。
使用上一节的示例,绘制闭环阶跃响应图:
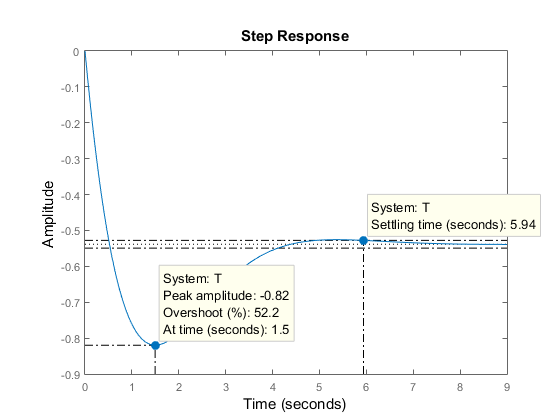
step(T)
现在,右键单击曲线图以显示峰值响应和稳定时间特性,并单击蓝点读取相应的过冲和稳定时间值:
五、分析 MIMO 系统
目前提到的所有命令都完全支持多输入多输出(MIMO)系统。在多输入多输出情况下,这些命令会生成数组图。例如,请看下面的两输入两输出系统。
sys = rss(3,2,2);
sys.A = [-0.5 -0.3 -0.2 ; 0 -1.3 -1.7; 0.4 1.7 -1.3];
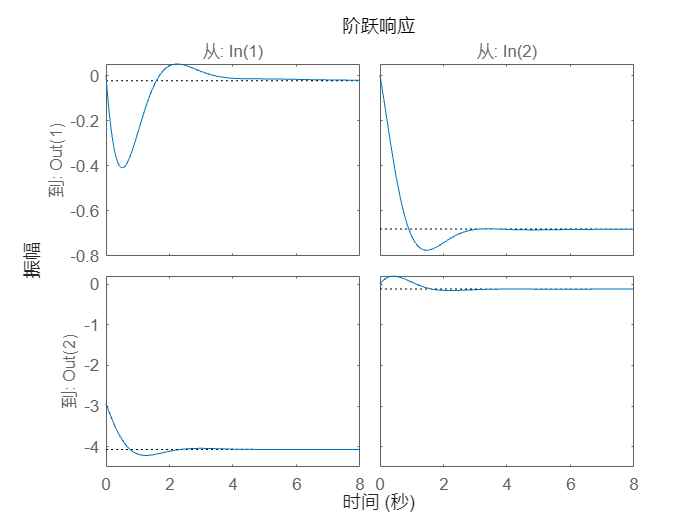
阶跃响应是一个 2×2 的图阵列,每列显示一个特定输入通道的阶跃响应。
step(sys)
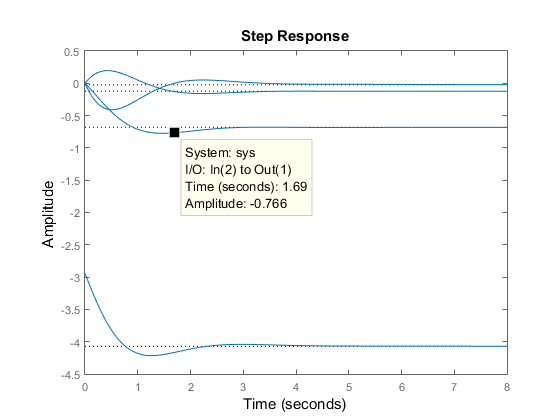
您可以右键单击曲线图并选择 I/O 分组 -> 全部子菜单,将所有四个响应组合到一个曲线图上。
以下附加图有助于分析多输入多输出系统:
-
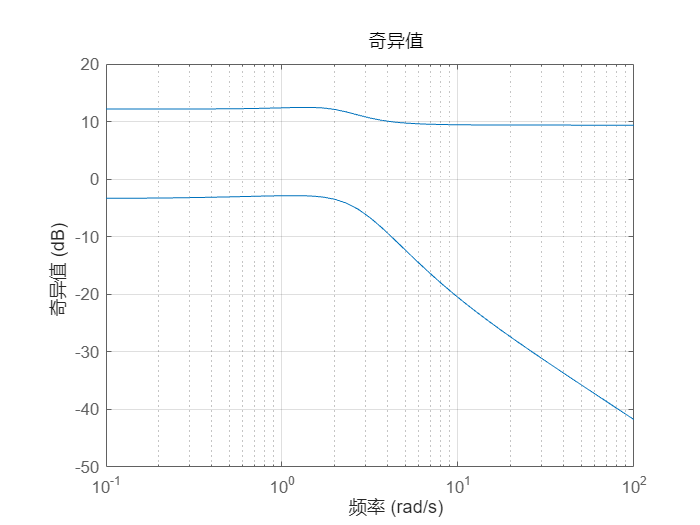
奇异值图 (sigma),显示频率响应的主要增益
-
每个 I/O 对的极点/零点图(iopzplot)
例如,绘制 sys 的峰值增益与频率的函数关系图:
sigma(sys)
grid
六、系统比较
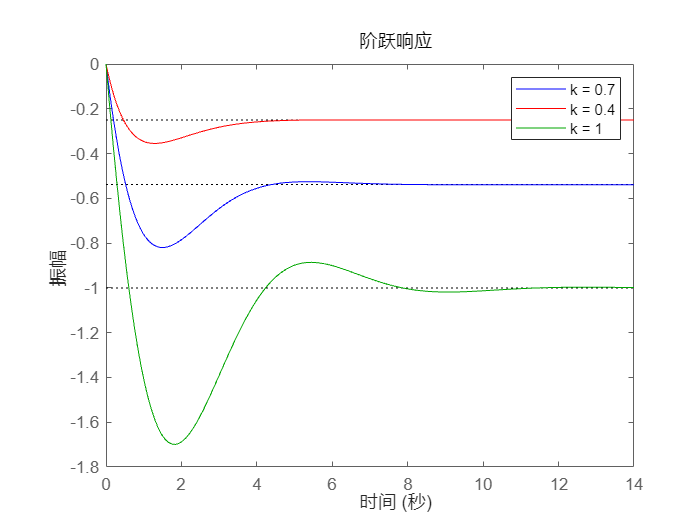
您可以使用任何响应绘图命令同时绘制多个系统。您可以为每个系统指定特定的颜色、标记或线条样式,以便于比较。以上述反馈为例,用三种不同颜色绘制环路增益 k 的三个值的闭环阶跃响应:
k1 = 0.4;
T1 = feedback(G*k1,1);
k2 = 1;
T2 = feedback(G*k2,1);
step(T,'b',T1,'r',T2,'g')
legend('k = 0.7','k = 0.4','k = 1')
七、修改时间轴或频率轴数值
您可以修改现有线性分析图的时间和频率向量。
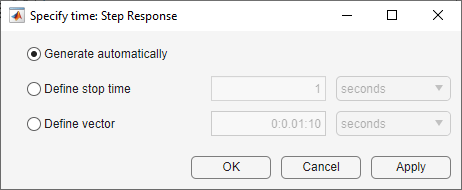
对于阶跃图和脉冲图,可以通过右键单击绘图区域并选择指定时间来指定时间矢量。
在 "指定时间 "对话框中,您可以使用以下方法之一定义时间值和单位。
-
自动生成 - 根据系统动态自动生成时间矢量。稀疏系统不支持此选项。
-
定义停止时间 - 指定停止时间,创建从时间 0 开始的时间矢量。
-
定义矢量 - 将时间指定为单调递增、间距均匀的时间值矢量。
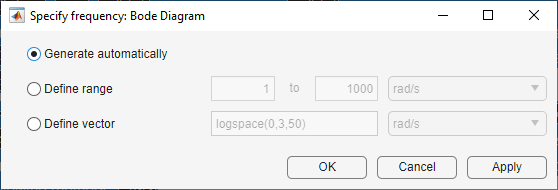
对于波特图、奈奎斯特图、尼克尔斯图和西格玛图,可以通过右键单击绘图区域并选择指定频率来指定频率矢量。
在 "指定频率 "对话框中,您可以使用以下方法之一定义频率值和单位。
-
自动生成 - 根据系统动态自动生成频率矢量。稀疏系统不支持此方法。
-
定义范围 - 指定频率范围。稀疏系统不支持此方法。
-
定义矢量 - 指定要绘制成矢量的频率。
如果您的系统是 frd 对象,则会在频率值之间插值绘制响应。
更改时间和频率单位将指定输入的单位,但不会更改绘图中的单位。