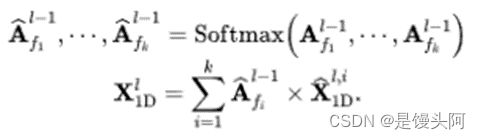7、TimesNet:一个通用的时间序列神经网络骨干
前言:
今天解读一篇文章:
名字:《TIMESNET: TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS 》
作者:
1.Introduction
本文中了 ICLR 2023,是清华软院龙明盛老师组的文章,本文的作者就是 Autoformer 的作者,所以本文的很多思想都延续了 Autoformer。不同于 Autoformer 只集中于时间序列预测,本文提出的 TimesNet 是一个通用的时间序列神经网络骨干,可处理各种不同的时间序列任务,如最常见的任务:预测、分类、异常检测等等。
2.Key Points
2.1 1D变2D
1维变2维:这是本文的核心。大部分现有方法都是作用于时间序列的时间维度,捕获时序依赖性。实际上,现实时间序列一般都有多种模式,比如不同的周期,各种趋势,这些模式混杂在一起。如果直接对原始序列的时间维度来建模,真正的时序关系很可能隐藏在这些混杂的模式中,无法被捕获。
本文考虑到:现实世界的时间序列通常具有多周期性,比如每天周期、每周周期、每月周期;而且每个周期内部的时间点是有依赖关系的(比如今天 1 点和 2 点),不同的相邻周期内的时间点也是有依赖关系的(比如今天 1 点和明天 1 点),作者提出将 1D 的时间维度 reshape 成 2D 的。
下图左侧的时间序列具有三个比较显著的周期性(Period 1、Period 2、Period 3),将其 reshape 成三种不同的 2D-variations。每个2D-variations 的每一列包含一个时间段(周期)内的时间点,每一行包含不同时间段(周期)内同一阶段的时间点。变成 2D-variations 之后,就可以采用 2D 卷积等方式来同时捕获时间段内部依赖和相邻时间段的依赖。
Fig1.时间序列的多周期性和时间二维变化。每个周期都有周期内变化和周期间变化。我们将原始的一维时间序列转化为基于多个周期的二维张量集合,从而统一了周期内和周期间的变化。
那么怎么确定时间序列中的周期性呢?采用傅里叶变换。给时间序列做傅里叶变换后,主要的周期会呈现对应的高幅值的频率分量。设定超参数 k,然后只取 top k 个最大的幅值对应的频率分量,即可得到 top k 个主要的周期,这和 Autoformer中的处理类似。
具体操作如下图,左侧是确定 top k 个周期,在此只画了三个,然后将 1D 的时间序列 reshape 成 3 种不同的 2D-variations(不能整除的可以用padding),对这三种 2D-variations 用 2D 卷积进行处理之后再聚合结果即可。
Fig2.用于说明时间序列中的二维结构的单变量示例。通过发现周期,我们可以将原来的一维时间序列转换成结构化的二维张量,从而方便地进行二维核处理。通过对时间序列的所有变量进行相同的重塑操作,我们可以将上述过程推广到多元时间序列。
为了统一表示周期内与周期间的时序变化,我们首先需要发掘时间序列的周期性。对于一个时间长度T、通道维度C的一维时间序列:
其周期性可以由时间维度的快速傅里叶变换FFT计算得到,即:
其中,A∈RT代表了X1D中每个频率分量的强度,强度最大的K个频率{f1,…,fk}对应着最显著的k个周期长度{p1,…,pk}。上述过程简单记为:
接下来,如上图所示,我们可以基于选定的周期对原始的一维时间序列X1D进行折叠,该过程可以形式化为:
其中,Padding()是在序列末尾补0,使得序列长度可以被pi整除。通过上述操作,我们得到了一组二维张量{X12D,…,Xk2D},Xk2D对应着由周期pi主导的二维时序变化。
但是,对于上述二维向量,其每列与每行分别对应着相邻的时刻与相邻的周期,而临近的时刻与周期往往蕴含着相似的时序变化。因此,上述二维张量会表现出二维局部性(2D locality),从而可以很容易通过2D卷积捕捉信息。
2.2 TimesBlock
得到 k 个 2D-variations之后该怎么处理呢?本文提出了 TimesBlock,每层 TimesBlock 又分为两步。首先是要先对这些 2D-variations 分别用 2D 卷积(可以是 ResNet、ConvNeXt 等)或者其他的视觉骨干网络(比如 Swin,Vit)处理;其次将 k 个处理后的结果再聚合起来。
对于第一步,本文采用了一种参数高效的 Inception block。Inception block 是GoogleNet 中的模块,包含多个尺度的 2D 卷积核。如下左图蓝色区域,处理 k 个 2D-variations 的 Inception block 是参数共享的。因此,模型整体的参数量不会随着超参数 k 的增大而增大,因此本文将其称为参数高效的Inception block(Parameter-efficient Inception block)。
Fig.3 TimesNet构架
对于第二步,在处理完 k 个 2D-variations 之后,需要将其展平回 1D-variations,并截断到原始长度 (这对应于前面不能整除时使用 padding 的情况,相当于把多余的 padding 给去掉)。总之,得到 k 个变换回去的 1D-variations 之后,该如何聚合这 k 个结果呢?
如上图右侧所示,也是延续 Autoformer 的思路,根据傅里叶变换后频率周期对应的赋值大小来加权聚合,幅值大的证明该频率周期的分量越显著也越重要,给它较大的聚合权重,幅值小的则相反。直接用 softmax 归一化这些幅值 ,然后将归一化后幅值作为加权权重来聚合上面得到的 k 个 1D-variations 即可。
模型详细处理机制如下:
TimesNet由堆叠的TimesBlock组成。输入序列首先经过嵌入层得到深度特征X01D∈RT*dmodel。对于第L层TimesBlock,其输入为Xl-11D∈RT*dmodel,之后通过2D卷积提取二维时序变化:
具体地, TimesBlock包含以下子过程:
1. 一维变二维:首先对输入的一维时序特征Xl-11D提取周期,并将其转换为二维张量来表示二维时序变化,即在上一节中所描述的过程:
2.提取二维时序变化表征:对于二维张量{Xl,12D,,,Xl,k2D},由于其具有二维局部性,因此,我们可以使用2D卷积提取信息。在这里,我们选取了经典的Inception模型,即:
3. 二维变一维:对于提取的时序特征,我们将其转化回一维空间以便进行信息聚合:
其中,![]() ,Trunc()表示把步骤1中的Padding()操作补充的0去掉。
,Trunc()表示把步骤1中的Padding()操作补充的0去掉。
4. 自适应融合:类似Autoformer中的设计,我们将得到的一维表征![]() 以其对应频率的强度进行加权求和,得到最终输出。
以其对应频率的强度进行加权求和,得到最终输出。
通过上述设计,TimesNet完成了“多个周期分别提取二维时序变化,再进行自适应融合”的时序变化建模过程。由于TimesNet将一维时序特征转换为二维张量进行分析,因此可以直接采用先进的视觉骨干网络进行特征提取,例如Swin Transformer、ResNeXt、ConvNeXt等。这种设计也使得时序分析任务可以直接受益于蓬勃发展的视觉骨干网络。