ら、缘未尽

基于Tensorflow搭建卷积神经网络实现经典手写数据集的分类问题

一 . 基本概念

卷积神经网络（Convolutional Neural Networks, CNN）是一类包含卷积计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一。卷积神经网络具有表征学习（representation learning）能力，能够按其阶层结构对输入信息进行平移不变分类（shift-invariant classification），因此也被称为“平移不变人工神经网络（Shift-Invariant Artificial Neural Networks, SIANN）”。

（1）.卷积神经网络和神经网络的区别

1.层级结构：

普通神经网络（全连接神经网络）：每个神经元与前一层的所有神经元相连接，层与层之间是全连接的。

卷积神经网络：主要由卷积层、池化层和全连接层组成。卷积层通过滤波器（卷积核）对输入进行卷积操作，提取局部特征。池化层对卷积层输出进行下采样，减小空间尺寸和参数量。全连接层将特征图展平为一维向量，并通过全连接层进行最终的分类或回归操作。

2.参数共享：

普通神经网络：每个神经元与前一层的所有神经元相连接，参数是独立的，没有共享。

卷积神经网络：卷积层中的滤波器（卷积核）在整个输入图像上进行卷积操作，参数是共享的。这样可以提取输入中的局部特征，并且可以在不同位置检测到相同的特征。

3.处理多维数据：

普通神经网络：适用于一维序列数据或具有固定尺寸的二维图像，需要将多维数据展平为一维向量输入。

卷积神经网络：专为处理多维数据设计，特别适用于处理二维图像。通过卷积和池化层，可以保留输入的空间结构和局部关联性。

（2）.卷积神经网络的应用

卷积神经网络在计算机视觉领域中取得了重大的突破，广泛用于图像分类、目标检测、图像分割等任务。相比普通神经网络，卷积神经网络能够更有效地处理图像数据，提取图像中的局部特征并保留空间信息。

二 . CNN各层操作原理及作用

1.卷积层（Convolutional Layer）：

卷积操作：卷积层通过使用一组可学习的滤波器（卷积核）对输入数据进行卷积操作。滤波器在输入数据上滑动并执行元素乘积累加，以提取输入数据的局部特征。卷积操作能够有效地捕捉输入数据中的空间相关性和局部模式。
特征图（Feature Map）：卷积操作的结果称为特征图，其中每个元素表示对应位置的特征激活值。通过使用多个不同的滤波器，卷积层可以提取多个特征图，每个特征图对应一种不同的特征。

2.池化层（Pooling Layer）：

池化操作：池化层通过对输入数据的局部区域进行下采样，减小数据的空间尺寸和参数数量。常见的池化操作包括最大池化和平均池化，它们分别选取局部区域的最大值或平均值作为池化操作的结果。
作用：池化操作可以减小数据的维度，保留重要的特征信息，并对输入数据的平移不变性提供一定程度的保护。

3.非线性激活函数（Activation Function）：

激活函数：卷积神经网络中的卷积层和全连接层之间通常会插入一个非线性激活函数，如ReLU（Rectified Linear Unit）激活函数。激活函数引入非线性变换，使网络能够学习非线性模式和复杂的决策边界。

4.全连接层（Fully Connected Layer）：

全连接层：卷积和池化层输出的特征图被展平为一维向量，并连接到一个或多个全连接层。全连接层的神经元与前一层的所有神经元相连接，每个神经元对应一个权重参数。全连接层将学习将输入特征映射到输出类别的映射关系。

5.后续层和损失函数：

后续层：卷积神经网络可以包含多个卷积层、池化层和全连接层，形成深层网络结构。通常在全连接层之后，可以添加更多的全连接层或其他类型的层，如Dropout层或BatchNormalization层，以增强网络的表达能力和泛化能力。

6.损失函数：

在分类问题中，常用的损失函数是交叉熵损失函数（Cross-Entropy Loss），用于衡量模型输出与真实标签之间的差异。在回归问题中，可以使用均方误差损失函数（Mean Squared Error Loss）等。

7.反向传播和优化算法：

反向传播：通过反向传播算法，根据损失函数计算的梯度信息，将梯度从输出层向前传播，更新网络中的权重和偏置，以最小化损失函数。
优化算法：常用的优化算法包括随机梯度下降（Stochastic Gradient Descent, SGD）、Adam、RMSprop等，用于根据梯度信息更新网络参数。

三 . 卷积神经网络为什么要卷积，卷积卷的是个啥？

卷积神经网络（Convolutional Neural Network, CNN）之所以使用卷积操作，是为了有效地处理具有网格结构的数据，特别是图像数据。卷积操作主要针对输入数据的局部特征进行提取和处理。

在卷积神经网络中，卷积操作是指通过使用一组可学习的滤波器（也称为卷积核）对输入数据进行卷积运算。滤波器是一个小的二维矩阵，它在输入数据上滑动并执行元素乘积累加的操作。

卷积操作的作用如下：

1.特征提取：通过卷积操作，滤波器能够在输入数据中寻找特定的局部特征。例如，对于图像数据，滤波器可以检测边缘、纹理、颜色等局部特征。

2.参数共享：卷积操作中的滤波器在整个输入数据上共享参数。这意味着同一个滤波器可以应用于输入的不同位置，从而可以检测到相同的特征，无论这些特征出现在图像的哪个位置。

3.减少参数量：由于参数共享的特性，卷积操作可以大大减少需要学习的参数数量，从而降低了模型的复杂性和计算开销。

通过卷积操作，卷积神经网络可以提取输入数据中的局部特征，并保留了输入数据的空间结构。卷积层的输出结果（特征图）可以输入到后续的层中进行进一步的处理和学习，如池化层和全连接层，最终实现对图像数据的分类、识别和分析。

四 . 使用的数据集介绍

本次实验使用的数据集是minist手写字体的数据集，训练集有六万张图片，像素为28*28的。测试集有一万张图片，像素为28*28。经过cnn训练，输出为0~9的其中之一的数字。

五 . python实战

Python环境：ANACONDA创建的python3.10，加Tensorflow库

搭建步骤：

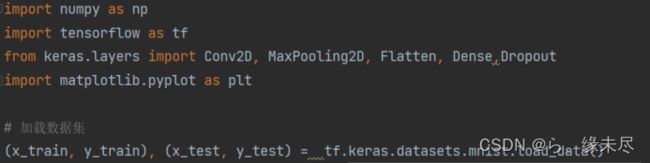
导入库和数据集
数据初始化和升维
搭建训练模型
编译模型和训练
评估模型

（1）.导入库和数据集

（2）.数据初始化和升维

这里解释一下为什么要升维，和为什么要转数据格式

1.通过将二维图像转换为四维张量，我们可以更方便地处理和传递图像数据到卷积神经网络的各个层。具体来说，在上述代码中，通过使用np.reshape函数将输入数据x_train和x_test从三维张量变为四维张量，分别具有形状(batch_size, height, width, 1)。更适合用于RGB这类图像的处理

2.在分类任务中，标签通常是表示类别的整数值。然而，神经网络的输出层通常采用softmax激活函数，它会将输出解释为概率分布。为了适应这种输出形式，我们将标签转换为one-hot编码。One-hot编码是一种将整数标签转换为二进制向量的表示方法，其中只有一个位置是1，其余位置都是0。每个位置对应一个类别，被编码的标签对应的位置设为1，其他位置设为0。在上述代码中，通过使用tf.keras.utils.to_categorical函数将训练集和测试集的标签从整数形式转换为one-hot编码。这样做是为了让标签符合神经网络输出层的要求，可以更好地进行概率预测和分类。

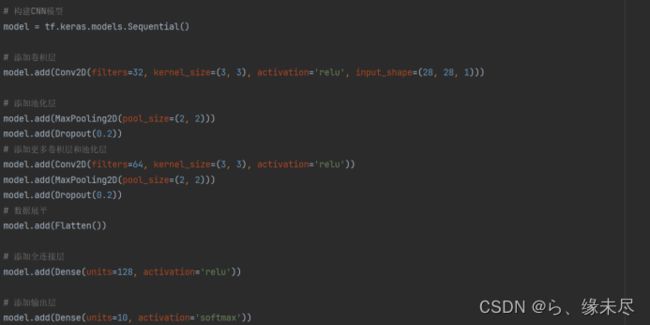
（3）.搭建训练模型

本次的训练模型中我们使用了一个卷积层加一个池化最后用Dropout优化防止过拟合，并使用了两次这样的组合，然后讲数据展平为一维数据进行后续的全连接层的计算，后面加了两个全连接层第一个用了500个神经元，第二个用了10个神经元来表示数据0-9

（4）.编译模型和训练

（5）评估模型

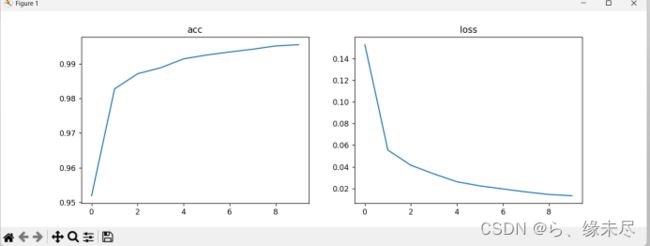
训练结果：

测试准确率为99.21%

下面是训练10次的损失函数和准确率的可视图

六 . 模型改进

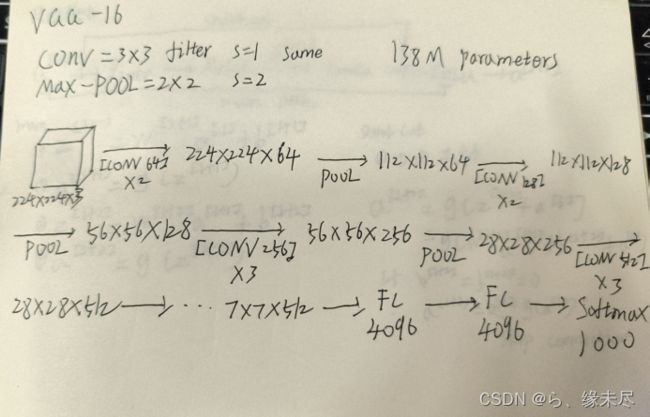
本次的实战我用了两个卷积层进行的，相对来说没那么深，于是我想如果深度更高是不是准确率更高，于是我找到了VGG-16模型，具有16个卷积层和3个全连接层，其中卷积层主要用于特征提取，全连接层用于分类。模型中的卷积层都使用小尺寸的卷积核（3x3）和步长为1，池化层使用2x2的最大池化。模型中的卷积层和全连接层之间都使用ReLU激活函数。

具体的实现方式如下图

由于VGG-16涉及的参数巨多，所以我缩小了一点

因此我对源代码进行了改进

import numpy as np
import tensorflow as tf
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense,Dropout
import matplotlib.pyplot as plt

# 加载数据集
(x_train, y_train), (x_test, y_test) =  tf.keras.datasets.mnist.load_data()

# 将像素值从0-255缩放到0-1之间
x_train = x_train.astype('float32') / 255
x_test = x_test.astype('float32') / 255

# 将标签转换为one-hot编码    神经网络的输出层通常采用softmax激活函数，它会将输出解释为概率分布。为了适应这种输出形式，我们将标签转换为one-hot编码。
y_train = tf.keras.utils.to_categorical(y_train, 10)
y_test = tf.keras.utils.to_categorical(y_test, 10)

# 将输入数据从2D数组reshape为4D张量
x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], x_train.shape[2], 1))
x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], x_test.shape[2], 1))


model = tf.keras.models.Sequential()

model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu', padding='same',input_shape=(28, 28, 1)))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(MaxPooling2D((2, 2), strides=(2, 2)))
model.add(Dropout(0.2))

model.add(Conv2D(filters=128, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(Conv2D(filters=128, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(MaxPooling2D((2, 2), strides=(2, 2)))
model.add(Dropout(0.2))

model.add(Conv2D(filters=256, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(Conv2D(filters=256, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(Conv2D(filters=256, kernel_size=(3, 3), activation='relu', padding='same'))
model.add(MaxPooling2D((2, 2), strides=(2, 2)))
model.add(Dropout(0.2))



model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dense(128, activation='relu'))
model.add(Dense(10, activation='softmax'))


model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['acc'])
history=model.fit(x_train, y_train, epochs=10, batch_size=32, validation_data=(x_test, y_test))
# 评估模型
test_loss, test_acc = model.evaluate(x_test, y_test)
print('Test accuracy:', test_acc)

#数据可视化
history.history.keys()
fig,axes=plt.subplots(1,2,figsize=(12,4))
axes[0].plot(history.epoch,history.history.get('acc'))
axes[0].set_title('acc')
axes[1].plot(history.epoch,history.history.get('loss'))
axes[1].set_title('loss')
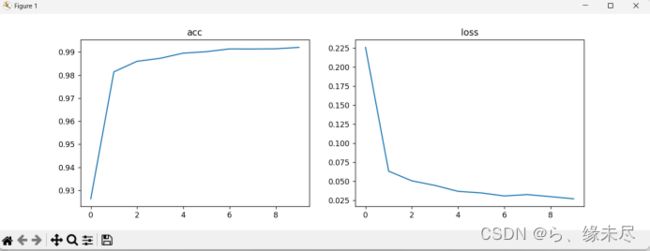
plt.show()

结果如下

测试准确率为99.36%,相比较于没优化的模型提高了0.15%