C++实现红黑树(含完整代码+图)
红黑树(C++实现)
一、红黑树的概念
红黑树是平衡二叉查找树(AVL)的变体,差异在于红黑树的左右子树高差有可能大于1,节点有红黑色之分。红黑树的平衡就是通过节点的红黑颜色进行调节。
二、红黑树的性质
1.每个节点不是红色就是黑色;
2.根节点为黑色;
3.所有叶子节点(NIL节点)是黑色;
4.如果节点为红色,子节点必须为黑色;
5.任一叶子节点到根节点路径上的黑色节点个数相等;
性质5可推出:
6.新增节点必须是红色;
性质4可推出:
7.新增节点的父节点必须是黑色;
三、红黑树的定义
3.1 红黑树节点定义
typedef int KEY_TYPE;
typedef int VALUE_TYPE;
#define RED 1
#define BLACK 2
typedef struct _rb_tree_node
{
unsigned char color;
struct _rb_tree_node* left;
struct _rb_tree_node* right;
struct _rb_tree_node* parent;
KEY_TYPE key;
VALUE_TYPE value;
} rbtree_node;
3.2 红黑树定义
typedef struct _rb_tree
{
rbtree_node* root;
rbtree_node* nil; /* 所有的空叶子节点(黑)共享一个节点 */
} rbtree;
四、红黑树的平衡操作(左旋、右旋)
4.1 左旋操作
以上图为例,左旋涉及到的主要节点有节点x和节点x的右子节点y。
涉及到的指针有节点x的父节点指针以及父节点指向x的指针,x指向右子节点y的指针以及节点y指向x的指针,y指向左子节点的指针以及左子节点指向y的指针。
变化操作主要有三步:
a.将y的左子树变成x节点的右子树;
b.节点y顶替节点x的位置;
c.将节点x变成节点y的左子节点。
4.2 左旋定义
/* 左旋 */
void rbtree_rotate_left(rbtree* T, rbtree_node* x)
{
// x为旋转点
rbtree_node* y = x->right; // 令y为旋转点的右子节点
/* 将节点y的左子树变为节点x的右子树 */
x->right = y->left;
if (y->left != T->nil)
{
y->left->parent = x;
}
/* 将节点y顶替节点x的位置,即节点x的父节点指向节点x的指针指向节点y */
y->parent = x->parent;
if (x == T->root) // 节点x为根节点
{
T->root = y;
}
else if (x == x->parent->left) // 节点x为父节点的左子节点
{
x->parent->left = y;
}
else // 节点x为父节点的右子节点
{
x->parent->right = y;
}
/* 将节点x变为节点y的左子节点 */
y->left = x;
x->parent = y;
}
4.3 右旋操作
右旋的主要节点为x,以及x的左子节点y。
涉及到的指针有节点x指向父节点的指针以及父节点指向x的指针,节点x指向左子节点y的指针以及节点y指向x的指针,节点y指向右子节点的指针以及右子节点指向y的指针。
变化操作主要有三步:
a.将节点y的右子树变成节点x的左子树;
b.节点y顶替节点x的位置;
c.将节点x变为节点y的右子节点。
4.4 右旋定义
/* 右旋 */
void rbtree_rotate_right(rbtree* T, rbtree_node* x)
{
// x为旋转点
rbtree_node* y = x->left; // 令y为旋转点的左子节点
/* 将节点y的右子树变为节点x的左子树 */
x->left = y->right;
if (y->right != T->nil)
{
y->right->parent = x;
}
/* 将节点y顶替节点x的位置,即节点x的父节点指向节点x的指针指向节点y */
y->parent = x->parent;
if (x == T->root) // 节点x为根节点
{
T->root = y;
}
else if (x == x->parent->right)
{
x->parent->right = y;
}
else
{
x->parent->left = y;
}
/* 将节点x变为节点y的左子节点 */
y->right = x;
x->parent = y;
}
五、红黑树的节点操作(插入、删除)
5.1 节点插入操作
首先考虑新节点插入的位置。由于红黑树已经是一个二叉搜索树,所以满足每个节点的值比左子节点的值大,比右子节点的值小。故可根据这个性质一直找到插入位置。
其次考虑插入节点的颜色。插入之前已经满足红黑树的性质,每插入一个黑色节点就会违背性质5,导致必须要调整子树;相反,如果插入红色节点,存在部分情况无需调整。那我们就更倾向将新插入的节点置为红色。
5.2 插入平衡操作
我们考虑新插入红色节点在哪种情况下需要进一步调整—即不满足第4条性质,父节点和子节点(新插入节点)同时为红色。
每种情况都涉及到三层节点,当前节点,父节点/叔父节点,祖父节点。具体有以下几种情况:
A.父节点为祖父节点的左子节点
a. 叔父节点为红色。此种情况最为简单,只需调节父节点、叔父节点、祖父节点的颜色即可。
b. 叔父节点为黑色,当前节点为父节点的右子节点。此种情况就需要将父节点作为旋转点进行左旋。完成之后转至情况1.c。
具体操作:以父节点为旋转点调用左旋函数z = z->parent;rbtree_rotate_left(T, z)(z = z->parent;这条语句可以保证新插入的点应该是两个连续红节点的下面一个节点即可)。

c. 叔父节点为黑色,当前节点为父节点的左子节点。此种情况需要将父节点和祖父节点作为主要节点进行右旋,并将原来的祖父节点黑色改红色,原来的父节点红色改黑色。
具体操作:将z节点的祖父节点置为红,父节点置为黑,以祖父节点为旋转点调用右旋函数rbtree_rotate_right(T, z->parent->parent);

B. 父节点为祖父节点的右子节点
a. 叔父节点为红色.此种情况只需调整父节点,叔父节点和祖父节点的颜色即可。
b. 叔父节点为黑色,当前节点为父节点的右子节点.此种情况就需要将当前节点和父节点作为主要节点,进行右旋。
c. 叔父节点为黑色,当前节点为父节点的左子节点.此种情况需要将父节点和祖父节点作为主要节点进行左旋,并将原来的祖父节点黑色改红色,原来的父节点红色改黑色。
5.3 节点插入定义
/* 插入 */
void rbtree_insert(rbtree* T, rbtree_node* z)
{
rbtree_node* x = T->root;
rbtree_node* y = T->nil;
/* 找到插入位置 */
while (x != T->nil)
{
y = x; /* 更新y的指向,保证y指向插入位置的父节点 */
if (z->key > x->key)
x = x->right;
else if (z->key < x->key)
x = x->left;
else
return;
}
z->parent = y;
if (y == T->nil) {
T->root = z;
}
else if (z->key < y->key)
y->left = z;
else
y->right = z;
/* 将新插入节点的子节点指向叶子节点 */
z->left = T->nil;
z->right = T->nil;
// 节点设置为红色
z->color = RED;
rbtree_insert_balance(T, z);
}
5.4 插入平衡定义
/* 平衡插入 */
void rbtree_insert_balance(rbtree* T, rbtree_node* z)
{
/* 不断向根节点递归判断 */
while (z != T->root && z->parent->color == RED) /* 父子节点皆为红色,不符合红黑树定义,得平衡操作 */
{
if (z->parent == z->parent->parent->left) /* 插入节点的父节点为左子节点 */
{
if (z->parent->parent->right->color == RED) /* 插入节点的叔父节点为红色 */
{
z->parent->parent->color = RED;
z->parent->color = BLACK;
z->parent->parent->right->color = BLACK;
z = z->parent->parent;
}
else /* 插入节点的叔父节点为黑色 */
{
if (z == z->parent->right) /* 插入节点为右子节点 */
{
z = z->parent;
rbtree_rotate_left(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_rotate_right(T, z->parent->parent);
}
}
else /* 插入节点的父节点为右子节点 */
{
if (z->parent->parent->left->color == RED) /* 插入节点的叔父节点为红色 */
{
z->parent->parent->color = RED;
z->parent->color = BLACK;
z->parent->parent->left->color = BLACK;
z = z->parent->parent;
}
else /* 插入节点的叔父节点为黑色 */
{
if (z == z->parent->left) /* 插入节点为左子节点 */
{
z = z->parent;
rbtree_rotate_right(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_rotate_left(T, z->parent->parent);
}
}
}
T->root->color = BLACK;
}
5.5 节点删除操作
删除具体思想:因为删除节点的位置随机性很大,有可能是叶子节点,也有可能是非叶子节点,也有可能是根节点,直接删除较为困难。故我们找一个容易删除的替换节点对其进行删除操作,而把替换节点数据覆盖删除节点的数据,就相当于删除了指定节点。下面详细介绍删除过程。
首先考虑删除节点的位置。由于红黑树是一个二叉搜索树,所以满足每个节点的值比左子节点的值大,比右子节点的值小。故可根据这个性质找到删除节点位置。
其次考虑替换节点的位置。替换节点,顾名思义,用来顶替删除节点的。有两种情况:1.删除节点为单支节点,则可以直接将子节点作为替换节点;2.删除节点有两个孩子节点,则取中序遍历的前驱节点作为替换节点。第二种情况其实可以保证找到的替换节点必然为单支节点或者叶子节点,进而转为情况1。找到替换节点之后,直接进行节点替换即可(节点的数据部分复制即可)。
接着考虑替换节点的颜色。注意我们实际删除的节点是替换节点。如果替换节点的颜色为红色,则删除前后都满足红黑树的性质,无需平衡操作;相反,如果替换节点为黑色,则删除之后其所在路径上的黑色节点数减一,有可能会不符合红黑树定义,需要平衡。
5.6 删除平衡操作
注意此时讨论平衡操作的基础情况是:替换节点为黑色 + 替换节点的删除已经完成。 此种情况需要进行平衡操作。
每种情况都涉及到三层节点:待平衡节点(已经完成删除的替换节点的孩子节点),父节点,兄弟节点,兄弟节点的孩子节点。具体有以下几种情况:
A.待平衡节点为红色。这种情况最为简单,直接将待平衡节点颜色置为黑色即可。

B.待平衡节点为黑色。
Ba.待平衡节点为父节点的左子节点
Baa.兄弟节点为红色。可以推出父节点一定为黑色。具体平衡操作:将父节点置为红色,兄弟节点置为黑色,以父节点作为旋转点进行左旋rbtree_rotate_left(T, x->parent); 更新待平衡节点的兄弟节点;转为其他情况判断。。。
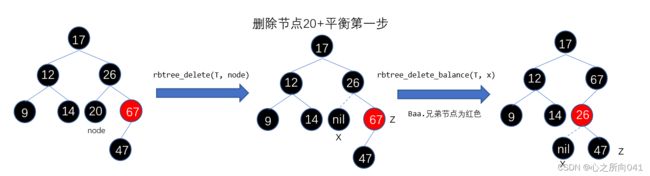
Bab.兄弟节点为黑色。
Baba.兄弟节点的两个孩子皆为黑色。具体操作;将兄弟节点置为红色;待平衡节点更新为自己的父节点;转为其他情况判断。。。
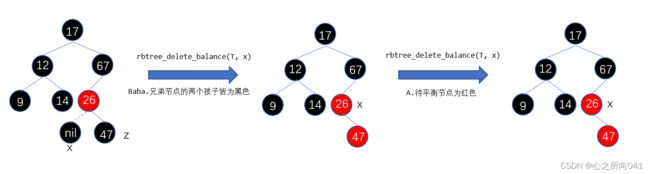
Babb.兄弟节点的右孩子黑,左孩子红。具体操作:将兄弟节点的左孩子颜色置黑;兄弟节点颜色置红;以兄弟节点作为旋转点进行右旋;更新待平衡节点的兄弟节点;转为其他情况判断。。。

Babc.兄弟节点的右孩子红。具体操作:将兄弟节点的颜色置为父节点的颜色;父节点的颜色置为黑色;兄弟的右孩子节点置为黑色;以父节点为旋转点进行左旋;将待平衡节点更新为根节点。恭喜平衡结束!!!

Bb.待平衡节点为父节点的右子节点。
Bba.兄弟节点为红色。可以推出父节点一定为黑色。具体操作:将父节点置为红色,兄弟节点置为黑色,以父节点作为旋转点进行右旋rbtree_rotate_right(T, x->parent); 更新待平衡节点的兄弟节点;转为其他情况判断。。。

Bbb.兄弟节点为黑色。
Bbba.兄弟节点的两个孩子皆为黑色。具体操作;将兄弟节点置为红色;待平衡节点更新为自己的父节点;转为其他情况判断。。。

Bbbb.兄弟节点的左孩子黑,右孩子红。具体操作:将兄弟节点的右孩子颜色置黑;兄弟节点颜色置红;以兄弟节点作为旋转点进行左旋rbtree_rotate_left(T, z);更新待平衡节点的兄弟节点;转为其他情况判断。。。

Bbbc.兄弟节点的左孩子红。具体操作:将兄弟节点的颜色置为父节点的颜色;父节点的颜色置为黑色;兄弟的左孩子节点置为黑色;以父节点为旋转点进行右旋rbtree_rotate_right(T, x->parent);将待平衡节点更新为根节点。恭喜平衡结束!!!

5.7 节点删除定义
/* 删除 */
rbtree_node* rbtree_delete(rbtree* T, rbtree_node* z)
{
rbtree_node* y = T->nil; /* 替换节点 */
rbtree_node* x = T->nil; /* 替换节点的孩子节点 */
/* 初始化替换节点 */
if ((z->left == T->nil) || (z->right == T->nil)) /* 删除节点z最多有一个孩子节点,替换节点y为删除节点z的孩子节点或者直接删除 */
{
y = z;
}
else /* 删除节点有两个孩子节点,替换节点y为中序遍历中的前驱节点 */
{
y = rbtree_successor(T, z);
}
/* 初始化替换节点的孩子节点x */
if (y->left != T->nil) {
x = y->left;
}
else if (y->right != T->nil)
{
x = y->right;
}
/* 删除替换节点,让孩子节点x顶替替换节点y */
x->parent = y->parent;
if (y == T->root) /* 替换节点y为根节点 */
{
T->root = x;
}
else if (y == y->parent->left) /* 替换节点y为左子节点 */
{
y->parent->left = x;
}
else /* 替换节点y为右子节点 */
{
y->parent->right = x;
}
/* 替换节点y数据覆盖删除节点z */
if (y != z) {
z->key = y->key;
z->value = y->value;
}
/* 替换节点为黑色,则所在路径上的黑色节点数减一,有可能会不符合红黑树定义,需要平衡 */
if (y->color == BLACK) {
rbtree_delete_balance(T, x);
}
return y;
}
5.8 删除平衡定义
/* 平衡删除 */
void rbtree_delete_balance(rbtree* T, rbtree_node* x) {
while ((x != T->root) && (x->color == BLACK)) /* B.待平衡节点为黑色 */
{
if (x == x->parent->left) /* A.待平衡节点为父节点的左子节点。(此时替换节点已经完成删除,由替换节点的 节点顶 替位置,子节点成为待平衡节点) */
{
rbtree_node *z = x->parent->right; /* 待平衡节点的兄弟节点 */
if (z->color == RED) /* Baa.兄弟节点z为红色。 */
{
z->color = BLACK;
x->parent->color = RED;
rbtree_rotate_left(T, x->parent);
z = x->parent->right;
}
/* Bab.兄弟节点为黑色 */
if ((z->left->color == BLACK) && (z->right->color == BLACK)) /* Baba.兄弟节点的两个孩子皆为黑色 */
{
z->color = RED;
x = x->parent;
}
else
{
if (z->right->color == BLACK) /* Babb.兄弟节点的右孩子黑,左孩子红 */
{
z->left->color = BLACK;
z->color = RED;
rbtree_rotate_right(T, z);
z = x->parent->right;
}
/* Babc.兄弟节点的右孩子红。 */
z->color = x->parent->color;
x->parent->color = BLACK;
z->right->color = BLACK;
rbtree_rotate_left(T, x->parent);
x = T->root;
}
/* b.待平衡节点为父节点的右子节点 */
rbtree_node *z = x->parent->left; /* Bba.兄弟节点为红色 */
if (z->color == RED)
{
z->color = BLACK;
x->parent->color = RED;
rbtree_rotate_right(T, x->parent);
z = x->parent->left;
}
/* Bbb.兄弟节点为黑色 */
if ((z->left->color == BLACK) && (z->right->color == BLACK)) /* Bbba.兄弟节点的两个孩子皆为黑色 */
{
z->color = RED;
x = x->parent;
}
else
{
if (z->left->color == BLACK) /* Bbbb.兄弟节点的左孩子黑,右孩子红 */
{
z->right->color = BLACK;
z->color = RED;
rbtree_rotate_left(T, z);
z = x->parent->left;
}
/* Bbbc.兄弟节点的左孩子红。 */
z->color = x->parent->color;
x->parent->color = BLACK;
z->left->color = BLACK;
rbtree_rotate_right(T, x->parent);
x = T->root;
}
}
}
x->color = BLACK; /* A.待平衡节点为红色 */
}
六、代码主函数
int main() {
int keyArray[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};
rbtree *T = (rbtree *)malloc(sizeof(rbtree));
if (T == NULL)
{
printf("malloc failed\n");
return -1;
}
T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
T->nil->color = BLACK;
T->root = T->nil;
rbtree_node *node = T->nil;
int i = 0;
for (i = 0;i < 20;i ++)
{
node = (rbtree_node*)malloc(sizeof(rbtree_node));
node->key = keyArray[i];
node->value = NULL;
rbtree_insert(T, node);
}
rbtree_traversal(T, T->root);
printf("----------------------------------------\n");
for (i = 0;i < 20;i ++)
{
rbtree_node *node = rbtree_search(T, keyArray[i]);
rbtree_node *cur = rbtree_delete(T, node);
free(cur);
rbtree_traversal(T, T->root);
printf("----------------------------------------\n");
}
return 0;
}
六、红黑树的优点及应用场景
6.1 红黑树的主要用途
1. 查询效率高。每个节点通常设置为键值对,通过快速查找到键,从而获取值。
eg:文件描述符-客户端id, 内存块组织
2. 有序数据。通过对红黑树的中序遍历可以得到一个有序的数据集。
eg:以时间排序的进程调度
6.2 应用场景
Epoll组件对监听的文件描述符fd集合用红黑树组织管理。
Epoll管理的文件描述符主要有两点要求:
1.文件描述符的数量不确定,可能很少,也可能很多;
2.能够尽快的找到触发的文件描述符。
这两种要求,红黑树都可很好的满足。


