并查集C++实现——算法设计与分析，含代码解释

什么是并查集

并查集简单来说是集合的集合，其中里层集合表示的节点都是可互相联通的，并查集有两种操作：

• union连接（并）：合并两个集合
• find查询（查）：查询两个元素是否在同一个集合

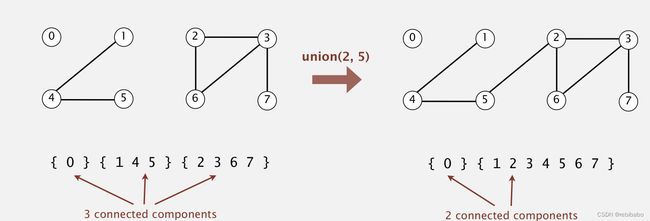
如下图所示，原来的并查集为$\{\{0\},\{1,4,5\},\{2,3,6,7\}\}$，$\{1,4,5\}$集合表示节点1、4、5可互相连通，经过合并2，5节点后，变成了右边的并查集，即$\{1,4,5\}$和$\{2,3,6,7\}$合并成了一个集合$\{1,2,3,4,5,6,7\}$

并查集的节点个数N可以很大，查询操作个数M也可能很大，并且合并和查询操作可以是混合在一起的。

接下来将介绍几种类型的并查集，最终将介绍一个优化的并查集，它只增加了几行代码就可以让性能提高很多。

quick-find并查集

我们用一个数组id来表示并查集，如果节点p和节点q是连接的，当且仅当它们的id相同，例如0,5,6是相连的，它们有共同的id = 0。

• union操作：将节点q和p合并，则需要遍历一遍整个id数组，将q所在集合的所有节点id改成p所在集合的id，时间复杂度为$O(N)$
• find操作：判断p和q是否相连只需要判断它们的id是否一样，时间复杂度为$O(1)$，所以是quick-find并查集。

上述并查集的代码如下：

#include 
#include 
using namespace std;
#define MAX 10004
 
class UnionFind {
    int id[MAX]; // 0 ~ 1000  记录上级/老大
    int minIndex; // 范围
    int maxIndex; // 范围
    int cnt; //连通分量的个数
 
public :
    UnionFind() {}
    UnionFind(int minIndex, int maxIndex) {
        this->minIndex = minIndex;
        this->maxIndex = maxIndex;
        this->cnt = maxIndex - minIndex + 1; // 连通分量的个数
        for (int i = minIndex; i <= maxIndex ; i++) {
            id[i] = i;		//初始化父节点指向自己 
        }
    }
 
    bool isConnected(int p, int q) {	//判断p和q是否相连 
    	cout << p << "和" << q << (id[p]==id[q]?"":"不") << "相连" << endl; 
        return id[p] == id[q];
    }
 
    bool connect(int p, int q) {		//合并x所在集合和y所在集合 
    	cout << "合并" << p << "和" << q << endl; 
    	int pid = id[p], qid = id[q];
        if (pid == qid) 	return false; // 已经在同一个set里面了，已经在同一个连通分量里面了
        for(int i = minIndex; i <= maxIndex; i++){		//将p所在集合的id改成q所在集合的id 
        	if(id[i] == pid)	
        		id[i] = qid;
		}
        cnt --; //连通分量少1
    }
    
    void show(){
    	for(int i = minIndex; i <= maxIndex; i++){
    		cout << "i:" << i << " id:" << id[i] << endl;
		}
	} 
};

int main() {
    class UnionFind uf(0,9);	//定义节点为0-9
    uf.connect(0,5);			//连接0和5节点 
    uf.connect(5,6);
 	uf.connect(1,2);
 	uf.connect(2,7);
 	uf.connect(1,6);
 	uf.connect(3,8);
 	uf.connect(3,4);
 	uf.connect(4,9);
 	uf.isConnected(4,0);	//查询4和0是否相连		
 	uf.isConnected(2,5);
 	uf.show();
} 

quick-union并查集

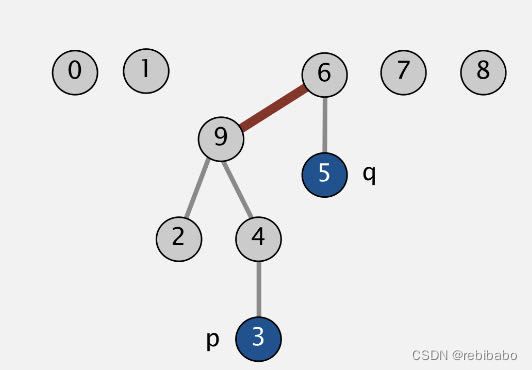
和quick-find的id数组表示含义不一样，quick-union的id数组表示它的父节点，根节点为$id[id[id[...id[i]]...]]]$，如下图所示，3号节点的父节点，即id为4，根节点为$id[id[id[3]]]=id[id[4]]=id[9]=9$。

union操作：合并p和q两个节点只需要将p的根节点id设置成q的根节点id即可，例如，将3和5合并，只需要将3的根节点id设置成5的根节点id即可，时间复杂度为$O(1)$，下图展示了Union操作

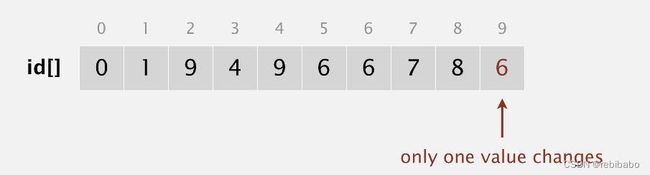
• find操作：查询p和q是否相连只需要判断p和q的根节点是否相同，最坏的情况查询根节点花费$O(N)$，也就是节点连成一条线的情况

代码表示如下：

#include 
#include 
using namespace std;
#define MAX 10004
 
class UnionFind {
    int id[MAX]; // 0 ~ 1000  记录上级/老大
    int minIndex; // 范围
    int maxIndex; // 范围
    int cnt; //连通分量的个数
 
public :
    UnionFind() {}
    UnionFind(int minIndex, int maxIndex) {
        this->minIndex = minIndex;
        this->maxIndex = maxIndex;
        this->cnt = maxIndex - minIndex + 1; // 连通分量的个数
        for (int i = minIndex; i <= maxIndex ; i++) {
            id[i] = i;		//初始化父节点指向自己 
        }
    }
 
 	int getRoot(int p){	//获得根节点id
 		while(p != id[p])	p = id[p];	//逐个向上遍历
 		return p;
	}
	
    bool isConnected(int p, int q) {	//判断p和q是否相连 
    	cout << p << "和" << q << (getRoot(p)==getRoot(q)?"":"不") << "相连" << endl; 
        return getRoot(p)==getRoot(q);
    }
 
    bool connect(int p, int q) {		//合并x所在集合和y所在集合 
    	cout << "合并" << p << "和" << q << endl; 
    	id[getRoot(p)] = getRoot(q);
        cnt --; //连通分量少1
    }
    
    void show(){
    	for(int i = minIndex; i <= maxIndex; i++){
    		cout << "i:" << i << " id:" << id[i] << endl;
		}
	} 
};

int main() {
    class UnionFind uf(0,9);	//定义节点为0-9
    uf.connect(0,5);			//连接0和5节点 
    uf.connect(5,6);
 	uf.connect(1,2);
 	uf.connect(2,7);
 	uf.connect(1,6);
 	uf.connect(3,8);
 	uf.connect(3,4);
 	uf.connect(4,9);
 	uf.isConnected(4,0);	//查询4和0是否相连		
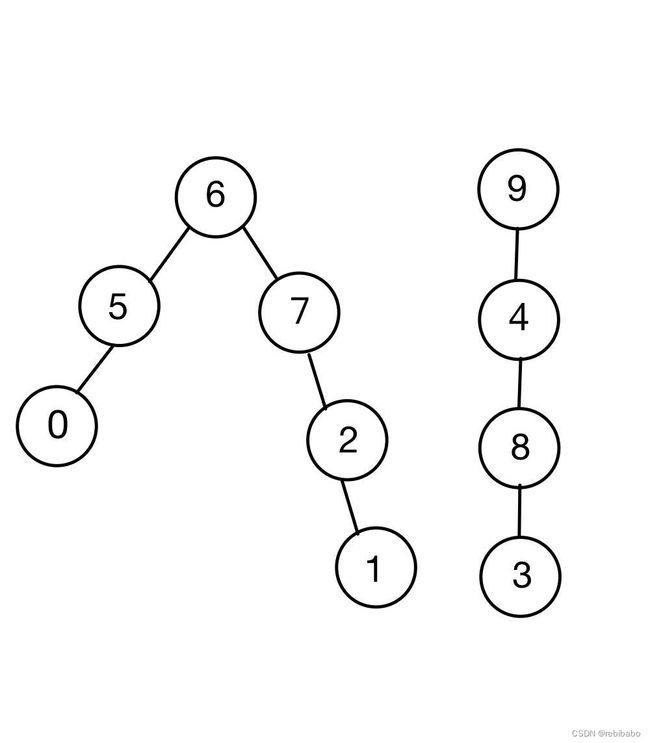
 	uf.isConnected(2,5);
 	uf.show();
} 

最后的id图和并查集（两棵树）如下两幅图所示，可以看出来深度还是挺大的，例如查询1和3节点的根节点需要查询3次，比较耗时。

优化一：增加权重比较使树变的平衡

这里的trick是把矮一点的树拼接到高一点的树，这样树的高度就不会增加，查询根节点就会更快

我们增加一个数组contain，contain[i]表示以i为根节点的子树的节点个数，初始条件下contain值全为1。

当我们拼接两棵树时，我们比较两棵树的contain值，将contain值小的树拼接到contain值大的树上，并且大树的contain值要加上小树的contain值，用代码表示如下：

int pRoot = getRoot(p);
int qRoot = getRoot(q);
if (qRoot == pRoot) {
    return false; // 已经在同一个set里面了，已经在同一个连通分量里面了
} 
else {
    if(contain[p] >= contain[q]) {
        id[qRoot] = pRoot;
        contain[pRoot] += contain[qRoot];
    } 
    else {
        id[pRoot] = qRoot;
        contain[qRoot] += contain[pRoot];
    }
}

这样修改以后，树的深度最多是$logN$，也就是说find操作的时间复杂度为$O(logN)$，union操作也为$O(logN)$，因为union需要寻找根节点，这样union操作和find操作的复杂度得到了中和。

优化二：路径压缩

当我们查询了一次节点p之后，我们求出了它的根节点root，我们可以p直接和root相连，这样我们下一次查找p的根节点就只要$O(1)$的时间了，我们就只需要在find操作里加两行代码即可，表示将当前节点与其父节点相连，直到与其根节点相连。

int getRoot(int p) {//采用递归的方式
    if (id[p] == p) {	//自己就是根节点 
    	return p;  
    } 
    else {
        int d = id[p];
        int root = getRoot(d);
        if (d != root) {
            id[p] = root;		//将当前节点的id设置成根节点 
            contain[d] -= contain[p]; 	//因为d的子树移到了根节点，所以要将d的contain减去p的contain 
    	}
    return root;
    }
}

初始的树如下所示：

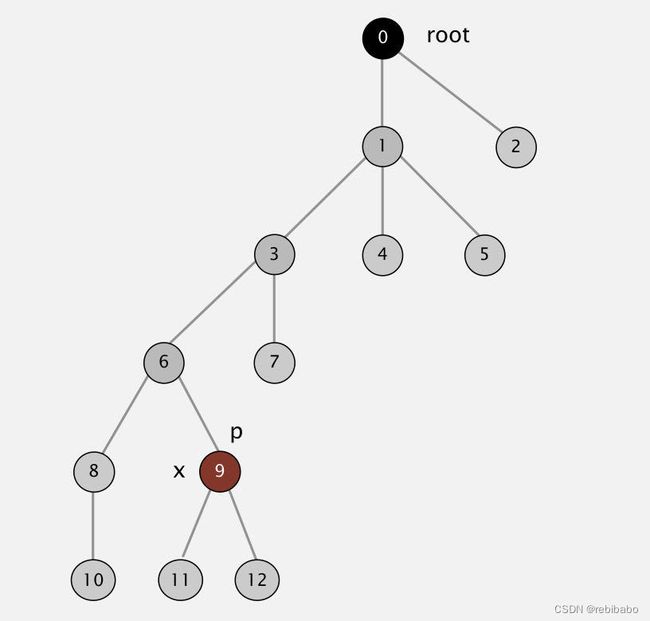
依次查询节点9，6，3以后，将它们移到根节点下，整棵树的高度就比之前少了很多，变得更平坦了。

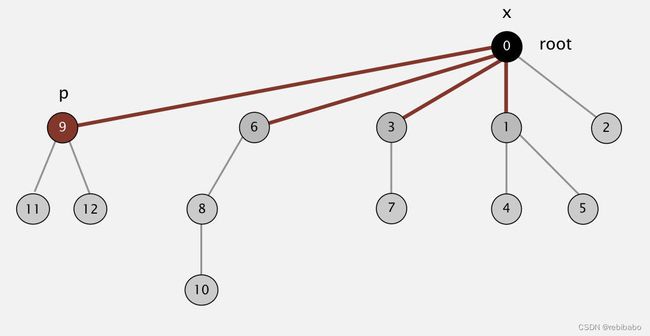
可以验证当有$10^9$次union操作和$10^9$次find操作，最普通的并查集需要花费30多年，而仅加上几行代码的优化过的并查集只需要6秒，由此可见一个性能好的算法是多么重要。

优化过后的代码

#include 
#include 
using namespace std;
#define MAX 10004
 
class UnionFind {
    int id[MAX]; // 
    int contain[MAX]; // 包含多少节点 
    int minIndex; // 范围
    int maxIndex; // 范围
    int cnt; //连通分量的个数
 
public :
    UnionFind() {}
    UnionFind(int minIndex, int maxIndex) {
        this->minIndex = minIndex;
        this->maxIndex = maxIndex;
        this->cnt = maxIndex - minIndex + 1; // 连通分量的个数
        for (int i = minIndex; i <= maxIndex ; i++) {
            id[i] = i;
            contain[i] = 1;
        }
 
    }
 
    int getRoot(int p) {//采用递归的方式 
        if (id[p] == p) {	//自己就是根节点 
            return p;  
        } 
		else {
            int d = id[p];
            int root = getRoot(d);
            if (d != root) {
                id[p] = root;		//将当前节点的id设置成根节点 
                contain[d] -= contain[p]; 	//因为d的子树移到了根节点，所以要将d的contain减去p的contain 
            }
            return root;
        }
    }
 
    bool isConnected(int p, int q) {
        return getRoot(q) == getRoot(p);
    }
 
    bool connect(int p, int q) {
 		int pRoot = getRoot(p);
		int qRoot = getRoot(q);
		if (qRoot == pRoot) {
		    return false; // 已经在同一个set里面了，已经在同一个连通分量里面了
		} 
		else {
		    if(contain[p] >= contain[q]) {
		        id[qRoot] = pRoot;
		        contain[pRoot] += contain[qRoot];
		    } 
		    else {
		        id[pRoot] = qRoot;
		        contain[qRoot] += contain[pRoot];
		    }
		}
        cnt --; //连通分量少1
    }
 
    int getCnt() {
        return cnt;
    }
 
    void show(){
    	cout << "i\tid\tcontain" << endl;
    	for(int i = minIndex; i <= maxIndex; i++){
    		cout << i << "\t" << id[i] << "\t" << contain[i] << endl;
		}
	} 
};
 
int main() {
    class UnionFind uf(1,6);	//定义节点为1-6 
    uf.connect(3,4);			//连接3和4节点 
    uf.connect(5,4);
 	uf.connect(1,2);
 	uf.connect(6,5);
 	uf.connect(1,5);
 	uf.getRoot(4);				//查找4的根节点 
 	uf.getRoot(2);
	uf.show();
}