FuSAGNet Running Analysis

1. Original Train Dataset

1.1 Shape of original train dataset

[ 0.935538 0.433560 1.0 1.0 … 0.000037 0.0 0.0 0.0 0.894236 0.434363 1.0 1.0 … 0.000037 0.0 0.0 0.0 0.952981 0.433002 1.0 1.0 … 0.000037 0.0 0.0 0.0 0.912204 0.434542 1.0 1.0 … 0.000037 0.0 0.0 0.0 0.922004 0.433872 1.0 1.0 … 0.000037 0.0 0.0 0.0 ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ ⋮ 0.958814 0.457039 1.0 1.0 … 0.000073 0.0 0.0 0.0 0.919379 0.457976 1.0 1.0 … 0.000073 0.0 0.0 0.0 0.911795 0.456012 1.0 1.0 … 0.000073 0.0 0.0 0.0 0.954614 0.455633 1.0 1.0 … 0.000073 0.0 0.0 0.0 0.898320 0.457418 1.0 1.0 … 0.000073 0.0 0.0 0.0 ] \begin{bmatrix} 0.935538 & 0.433560 & 1.0 & 1.0 & \ldots & 0.000037 & 0.0 & 0.0 & 0.0 \\ 0.894236 & 0.434363 & 1.0 & 1.0 & \ldots & 0.000037 & 0.0 & 0.0 & 0.0 \\ 0.952981 & 0.433002 & 1.0 & 1.0 & \ldots & 0.000037 & 0.0 & 0.0 & 0.0 \\ 0.912204 & 0.434542 & 1.0 & 1.0 & \ldots & 0.000037 & 0.0 & 0.0 & 0.0 \\ 0.922004 & 0.433872 & 1.0 & 1.0 & \ldots & 0.000037 & 0.0 & 0.0 & 0.0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0.958814 & 0.457039 & 1.0 & 1.0 & \ldots & 0.000073 & 0.0 & 0.0 & 0.0 \\ 0.919379 & 0.457976 & 1.0 & 1.0 & \ldots & 0.000073 & 0.0 & 0.0 & 0.0 \\ 0.911795 & 0.456012 & 1.0 & 1.0 & \ldots & 0.000073 & 0.0 & 0.0 & 0.0 \\ 0.954614 & 0.455633 & 1.0 & 1.0 & \ldots & 0.000073 & 0.0 & 0.0 & 0.0 \\ 0.898320 & 0.457418 & 1.0 & 1.0 & \ldots & 0.000073 & 0.0 & 0.0 & 0.0 \\ \end{bmatrix} ​0.9355380.8942360.9529810.9122040.922004⋮0.9588140.9193790.9117950.9546140.898320​0.4335600.4343630.4330020.4345420.433872⋮0.4570390.4579760.4560120.4556330.457418​1.01.01.01.01.0⋮1.01.01.01.01.0​1.01.01.01.01.0⋮1.01.01.01.01.0​……………⋱……………​0.0000370.0000370.0000370.0000370.000037⋮0.0000730.0000730.0000730.0000730.000073​0.00.00.00.00.0⋮0.00.00.00.00.0​0.00.00.00.00.0⋮0.00.00.00.00.0​0.00.00.00.00.0⋮0.00.00.00.00.0​ ​

• The shape is [47520, 51]

2. TimeDataset

• The final return

class TimeDataset(Dataset):
	pass
	def __getitem__(self, idx):
		pass
		return window, window_y, label, edge_index

• window: [51, 5]
• window_y: [51]
• label: [51]
• edge_index: [2, 2550]

2.1 Shape of train TimeDataset

• This is train_dataset which used to generate train_dataloader
• In train_dataloader author use random to split train subset and valid subset
• Therefore, we will get different train and valid dataset in every signal training

[ [ [ 9.5726 e − 01 4.5503 e − 02 ⋮ 5.8423 e − 01 ] t [ 9.1500 e − 01 4.7642 e − 02 ⋮ 2.0000 e − 01 ] t + 1 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 2 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 3 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 4 ] t r a i n [ 9.6824 e − 01 4.7642 e − 02 ⋮ 0.0000 e + 00 ] t a r g e t t + 5 [ [ 9.5726 e − 01 4.5503 e − 02 ⋮ 5.8423 e − 01 ] t + 1 [ 9.1500 e − 01 4.7642 e − 02 ⋮ 2.0000 e − 01 ] t + 2 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 3 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 4 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 5 ] t r a i n [ 9.6824 e − 01 4.7642 e − 02 ⋮ 0.0000 e + 00 ] t a r g e t t + 6 ⋮ ⋮ ] \begin{bmatrix} \begin{bmatrix} \begin{bmatrix} 9.5726e-01 \\ 4.5503e-02 \\ \vdots \\ 5.8423e-01 \\ \end{bmatrix}^{t} & \begin{bmatrix} 9.1500e-01 \\ 4.7642e-02 \\ \vdots \\ 2.0000e-01 \\ \end{bmatrix}^{t+1} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+2} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+3} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+4} \end{bmatrix} _{train} & \begin{bmatrix} 9.6824e-01 \\ 4.7642e-02 \\ \vdots \\ 0.0000e+00 \\ \end{bmatrix}^{t+5} _{target} \\ \begin{bmatrix} \begin{bmatrix} 9.5726e-01 \\ 4.5503e-02 \\ \vdots \\ 5.8423e-01 \\ \end{bmatrix}^{t+1} & \begin{bmatrix} 9.1500e-01 \\ 4.7642e-02 \\ \vdots \\ 2.0000e-01 \\ \end{bmatrix}^{t+2} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+3} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+4} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+5} \end{bmatrix} _{train} & \begin{bmatrix} 9.6824e-01 \\ 4.7642e-02 \\ \vdots \\ 0.0000e+00 \\ \end{bmatrix}^{t+6} _{target} \\ \vdots & \vdots \end{bmatrix} ​ ​ ​9.5726e−014.5503e−02⋮5.8423e−01​ ​t​ ​9.1500e−014.7642e−02⋮2.0000e−01​ ​t+1​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+2​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+3​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+4​ ​train​ ​ ​9.5726e−014.5503e−02⋮5.8423e−01​ ​t+1​ ​9.1500e−014.7642e−02⋮2.0000e−01​ ​t+2​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+3​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+4​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+5​ ​train​⋮​ ​9.6824e−014.7642e−02⋮0.0000e+00​ ​targett+5​ ​9.6824e−014.7642e−02⋮0.0000e+00​ ​targett+6​⋮​ ​

3. Add guassian noise

3.1 Source code

• This function purpose on adding noise to train data

x = torch.add(x, generate_gaussian_noise(x))

def generate_gaussian_noise(x, mean=0.0, std=1.0):
    eps = torch.randn(x.size()) * std + mean
    return eps

[ [ [ 9.5726 e − 01 4.5503 e − 02 ⋮ 5.8423 e − 01 ] t [ 9.1500 e − 01 4.7642 e − 02 ⋮ 2.0000 e − 01 ] t + 1 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 2 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 3 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 4 ] t r a i n + [ n o i s e ] [ 9.6824 e − 01 4.7642 e − 02 ⋮ 0.0000 e + 00 ] t a r g e t t + 5 [ [ 9.5726 e − 01 4.5503 e − 02 ⋮ 5.8423 e − 01 ] t + 1 [ 9.1500 e − 01 4.7642 e − 02 ⋮ 2.0000 e − 01 ] t + 2 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 3 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 4 [ 9.7511 e − 01 4.4018 e − 02 ⋮ 6.0243 e − 01 ] t + 5 ] t r a i n + [ n o i s e ] [ 9.6824 e − 01 4.7642 e − 02 ⋮ 0.0000 e + 00 ] t a r g e t t + 6 ⋮ ⋮ ] \begin{bmatrix} \begin{bmatrix} \begin{bmatrix} 9.5726e-01 \\ 4.5503e-02 \\ \vdots \\ 5.8423e-01 \\ \end{bmatrix}^{t} & \begin{bmatrix} 9.1500e-01 \\ 4.7642e-02 \\ \vdots \\ 2.0000e-01 \\ \end{bmatrix}^{t+1} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+2} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+3} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+4} \end{bmatrix} _{train} + \begin{bmatrix} noise \end{bmatrix} & \begin{bmatrix} 9.6824e-01 \\ 4.7642e-02 \\ \vdots \\ 0.0000e+00 \\ \end{bmatrix}^{t+5} _{target} \\ \begin{bmatrix} \begin{bmatrix} 9.5726e-01 \\ 4.5503e-02 \\ \vdots \\ 5.8423e-01 \\ \end{bmatrix}^{t+1} & \begin{bmatrix} 9.1500e-01 \\ 4.7642e-02 \\ \vdots \\ 2.0000e-01 \\ \end{bmatrix}^{t+2} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+3} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+4} & \begin{bmatrix} 9.7511e-01 \\ 4.4018e-02 \\ \vdots \\ 6.0243e-01 \\ \end{bmatrix}^{t+5} \end{bmatrix} _{train} + \begin{bmatrix} noise \end{bmatrix} & \begin{bmatrix} 9.6824e-01 \\ 4.7642e-02 \\ \vdots \\ 0.0000e+00 \\ \end{bmatrix}^{t+6} _{target} \\ \vdots & \vdots \end{bmatrix} ​ ​ ​9.5726e−014.5503e−02⋮5.8423e−01​ ​t​ ​9.1500e−014.7642e−02⋮2.0000e−01​ ​t+1​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+2​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+3​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+4​ ​train​+[noise​] ​ ​9.5726e−014.5503e−02⋮5.8423e−01​ ​t+1​ ​9.1500e−014.7642e−02⋮2.0000e−01​ ​t+2​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+3​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+4​ ​9.7511e−014.4018e−02⋮6.0243e−01​ ​t+5​ ​train​+[noise​]⋮​ ​9.6824e−014.7642e−02⋮0.0000e+00​ ​targett+5​ ​9.6824e−014.7642e−02⋮0.0000e+00​ ​targett+6​⋮​ ​

4. Forward of FuSAGNet

4.1. Forward of SparseEncoder

• We put x into Sparse Encoder and then get Sparse Matrix z
  $${\left[\begin{array}{c}32,51,5\end{array}\right]}_x==>\left[\begin{array}{c}32,51,5\end{array}\right]$$

4.1.1. Flattening x to 1 dim

x = x.view(B, -1)  # B = batch

Original x is: $$\left[\begin{array}{c}51,5\end{array}\right]$$
After converting, the shape of x is: $$\left[\begin{array}{c}255\end{array}\right]$$

4.1.2. Passing Sparse Encoder

Shape of x:
$$\left[\begin{array}{c}255\end{array}\right]$$
Layer of Encoder:

and now we get z
x_reconstruction come out Decoder

4.1.3 Passing Sparse Decoder

Same as above
And reshape x_recon:

x_recon = x_recon.view(x.size())

Final shape of x_recon:
$$\left[\begin{array}{c}32,51,5\end{array}\right]$$

4.1.4 GDN forwarding

Input:
$$z\left[\begin{array}{c}1632,5\end{array}\right]$$
Notice: z has been reshaped
Output:
$$gcnout\left[\begin{array}{c}1632,64\end{array}\right]$$
x:
$$\left[\begin{array}{c}32,51,64\end{array}\right]$$

4.1.5 OutLayer forwarding

Just a MLP layer
neure number = 64
Final Output:
$$\left[\begin{array}{c}32,51,1\end{array}\right]$$
After reshape:
Shape of out:
$$\left[\begin{array}{c}32,51\end{array}\right]$$
Finally, this is $$\hat{x}$$

5. Calculating Loss

loss_frcst = torch.sqrt(F.mse_loss(x_hat, y, reduction=reduction))
loss_recon = F.mse_loss(x_recon, x, reduction=reduction)
loss_recon += beta * kl_divergence(rhos, rho_hat)
loss = alpha * loss_frcst + (1.0 - alpha) * loss_recon
loss.backward()
optimizer.step()

6. Work

Final result:

F1: 0.7898 | Pr: 0.9795 | Re: 0.6618

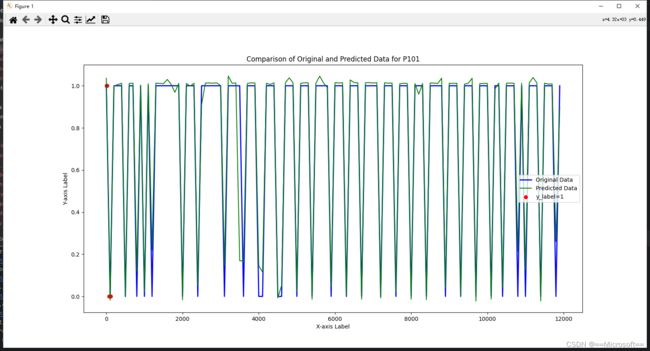
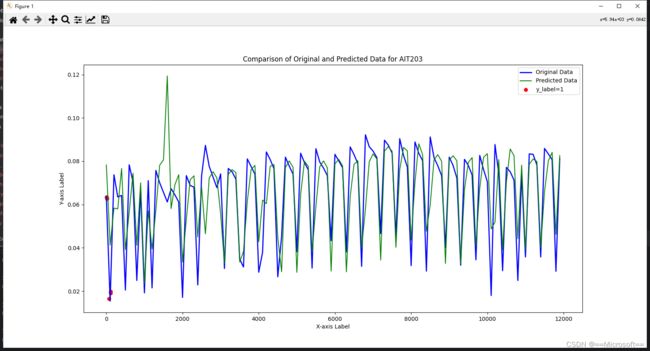
6.1 Charts

 python .\analysis\draw_chart.py -c 0 -n FIT101 -s 0 -e 12000 -ss 100 -o forecasting

7. Evaluate

7.1 Show result

(torchgpu) PS C:\Users\Nahida\Desktop\git\FuSAGNet> python .\main.py
[E 1/50] V: 1.7962 | F: 0.0783 | R: 0.3441 | beta*KLD: 0.001381228445097804
./pretrained/swat/best_11_01_21_39_51.pt
[E 2/50] V: 1.3167 | F: 0.0716 | R: 0.3172 | beta*KLD: 0.0007697785040363669
./pretrained/swat/best_11_01_21_39_51.pt
[E 3/50] V: 1.0857 | F: 0.0790 | R: 0.3142 | beta*KLD: 0.00041777745354920626
./pretrained/swat/best_11_01_21_39_51.pt
[E 4/50] V: 1.1425 | F: 0.0697 | R: 0.3145 | beta*KLD: 0.00039264175575226545
[E 5/50] V: 1.0713 | F: 0.0643 | R: 0.3042 | beta*KLD: 0.000236138905165717
./pretrained/swat/best_11_01_21_39_51.pt
[E 6/50] V: 1.1490 | F: 0.0840 | R: 0.2941 | beta*KLD: 0.00019004508794751018
[E 7/50] V: 1.0408 | F: 0.0691 | R: 0.3043 | beta*KLD: 0.00031222423422150314
./pretrained/swat/best_11_01_21_39_51.pt
[E 8/50] V: 1.1052 | F: 0.0726 | R: 0.3072 | beta*KLD: 0.0003566330997273326
[E 9/50] V: 1.0380 | F: 0.0638 | R: 0.2977 | beta*KLD: 0.0001942641392815858
./pretrained/swat/best_11_01_21_39_51.pt
[E 10/50] V: 1.1313 | F: 0.0691 | R: 0.2967 | beta*KLD: 0.0001202641287818551
[E 11/50] V: 1.1759 | F: 0.0648 | R: 0.2819 | beta*KLD: 0.0003031042870134115
[E 12/50] V: 1.0903 | F: 0.0651 | R: 0.3129 | beta*KLD: 0.0001659395929891616
[E 13/50] V: 1.1478 | F: 0.0728 | R: 0.3058 | beta*KLD: 0.0001352614490315318
[E 14/50] V: 1.0795 | F: 0.0553 | R: 0.2991 | beta*KLD: 0.00018071764498017728
[E 15/50] V: 1.0497 | F: 0.0676 | R: 0.3064 | beta*KLD: 0.00013218405365478247
./pretrained/swat/best_11_01_21_39_51.pt
[E 20/50] V: 1.0856 | F: 0.0641 | R: 0.3013 | beta*KLD: 0.00011476626968942583
[E 21/50] V: 1.0056 | F: 0.0597 | R: 0.3012 | beta*KLD: 9.098529699258506e-05
[E 22/50] V: 1.0465 | F: 0.0694 | R: 0.2984 | beta*KLD: 9.294903429690748e-05
[E 23/50] V: 1.1227 | F: 0.0630 | R: 0.3008 | beta*KLD: 0.00011197870480827987
[E 24/50] V: 1.0902 | F: 0.0665 | R: 0.2986 | beta*KLD: 6.557066808454692e-05
[E 25/50] V: 1.0708 | F: 0.0699 | R: 0.2979 | beta*KLD: 0.00015085433551575989
[E 26/50] V: 1.1226 | F: 0.0710 | R: 0.2998 | beta*KLD: 0.00017875805497169495
[E 27/50] V: 1.0242 | F: 0.0674 | R: 0.2902 | beta*KLD: 7.685294258408248e-05
[E 28/50] V: 1.0153 | F: 0.0726 | R: 0.3019 | beta*KLD: 0.00010462012141942978
[E 29/50] V: 0.9598 | F: 0.0722 | R: 0.2969 | beta*KLD: 7.716065738350153e-05
F1: 0.7962 | Pr: 0.9702 | Re: 0.6752
Save result at ./test_result1.pkt, please check

7.2. Calc score

7.2.1. Passing a function get_full_err_scores() to get all_normals and all_scores

7.2.2. Weighted Harmonic Mean

test_scores_f, _ = get_full_err_scores(test_result_f[:2], val_result_f[:2])
test_scores_r, _ = get_full_err_scores(test_result_r[:2], val_result_r[:2])

def whm(x1, x2, w1, w2):
    epsilon = 1e-2
    return (w1 + w2) * (x1 * x2) / (w1 * x2 + w2 * x1 + epsilon)

这段代码定义了一个名为 whm 的函数，用于计算加权谐波均值（Weighted Harmonic Mean）。加权谐波均值是一种统计方法，用于计算一组值的均值，其中每个值都有一个权重。在这个函数中，它接受两个值 x1 和 x2，以及它们对应的权重 w1 和 w2。
计算公式为：
Weighted Harmonic Mean
其中，x1 和 x2 是待计算的值，w1 和 w2 是它们的权重。epsilon 是一个小的正数，通常用于避免除零错误。计算结果是一组值的加权谐波均值。
加权谐波均值的计算方法通常用于多个数值的集合，其中每个值都有不同的重要性或权重。这有助于更好地反映数据中不同值的相对影响。

7.2.3. Use whm and ground truth calc a threshold

The final threshold is a specific number

7.2.4. Judge whether attacked or normal

 pred_labels[total_topk_err_scores > threshold] = 1

total_topk_err_scores = np.sum(
    np.take_along_axis(total_err_scores, topk_indices, axis=0), axis=0
)

• total_topk_err_score come from here

• The shape of total_topk_err_score is same as timestamp [44986]

• 总的来说，total_topk_err_scores 存储了从 total_err_scores 中选择的特定元素的和。这通常用于后续的数据处理和分析。

• total_err_score is whm

7.2.5. Calc precision, recall and auc

pre = precision_score(gt_labels, pred_labels)
rec = recall_score(gt_labels, pred_labels)
auc_score = roc_auc_score(gt_labels, total_topk_err_scores)