2022 International Collegiate Programming Contest, Jinan Site C. DFS Order 2(树形dp+回滚背包)

题目

n(n<=500)个点的树，是一棵以1为根的有根树，

你需要输出一个n*n的矩阵，

(i,j)表示点i在dfs序中是第j个被访问的节点的方案数

答案对998244353取模

思路来源

官方题解+严格鸽博客

2022 ICPC 济南站 C (回退背包) - 知乎

题解

官方题解是上面这样写的

感觉参考了这个方法的一部分，也参考了严格鸽方法的一部分，

结合二者，也用了一下自己统计的方法

1. 求总方案数

h[i]表示只考虑i的子树里的点时，dfs序的方案数

自然是子树中每个点直连儿子个数的乘积，

也就是，先令h[u]=1，对于u的每个直连儿子来说，h[u]*=h[v]，

再h[u]*=m!，其中m为u的直连儿子个数

2. 求只考虑u这棵子树时，把u的若干个儿子v看成(1,sz[v])，

第一维表示是一个直连儿子，第二维表示这个儿子的子树大小

因为访问一个直连儿子，紧接着就要访问这个儿子内子树的所有点

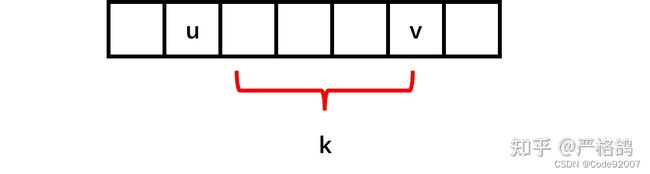
考虑怎么算出，dfs序中，u到v的距离恰为k的方案数

g[k+1]表示dfs序中u到v的距离恰为k+1的方案数

此时仅考虑u的子树中的点，由于每搜到u都需要重做一遍，所以第一维可以滚动掉

则需要u到v中放入k个点，这些点是由u的i个直连儿子(不包括v)贡献的，

i个儿子的子树大小总共为k

所以，计f[i][j]表示考虑u的子树，选了i个儿子，这i个儿子的子树大小为j的方案数，

先做一个背包，求出f数组，而注意到背包本质，是若干个多项式相乘

背包中的一个方案，对于选法来说，是无序的

dfs序中，则是不同的方案，所以需要将k个直连儿子乘上顺序，乘以k!

计m为u的直连儿子的总个数，剩下m-1-k个儿子也需要顺序，乘以(m-1-k)!

直连儿子v的子树中的点，也是需要乘以对应的顺序的，

不妨u的直连儿子是v,v1,v2,v3,v4，则需要再乘以h[v1]*h[v2]*h[v3]*h[v4]

而这等于h[u]/m!/h[v]，有以下伪代码：

for i: // 枚举u的直连儿子选了i个

    for k: // 枚举i个直连儿子的总子树大小是k

g[k+1]+=f[i][k]*(h[u]/m!/h[v])

求出g数组后，只是确定了(u,v)之间的距离，

对于v来说，需要确定与直连父亲的距离、父亲的父亲的距离、...

也就是需要求v与祖先这条链上每个点之间的距离，才能确定最终在dfs序数组中的位置

所以，计dp[i][j]为点i在dfs序中的位置为j的方案数（不考虑i子树内部的方案时）

按链从上往下合并g数组，即做一次背包的合并即可，有以下伪代码：

for i: // 枚举u在dfs序中的位置i

    for j:// 枚举u和v在dfs序中的距离j

          dp[v][i+j]+=dp[u][i]*g[j] // v在dfs序中的位置为i+j

这和最终所求，只查i子树内部的方案，所以，dp[i][j]*h[i]即为所求

这样暴力做的复杂度是的，因为上文提到的f数组的转移不包括v

对于u来说，枚举每个v的时候，都重新做一遍f的背包，复杂度

①对于所有直连儿子维护前缀背包和后缀背包，再合并前缀和后缀，

是不可行的，因为合并两个背包的复杂度还是

②线段树分治维护每个点的出现时间

应该可行，因为点v只会在v对应的子树这一段连续的区间内消失，

也就是两段存在的区间，最多做4次背包内加减物品的变化，但太难写了

③背包减物品=回滚背包，所以不如直接写回滚背包

背包本质是若干个多项式相乘，加一个物品乘一个多项式，

那么，减一个物品时，除以这个多项式即可，

具体来说，加的时候是逆序遍历从大到小加的，减的时候就正序遍历从小到大减

for(auto &v:e[u]){
        for(int i=m;i>=1;--i){
            for(int j=sz[u];j>=sz[v];--j){
                f[i][j]+=f[i-1][j-sz[v]];
            }
        }
    }

算g数组和dp数组之前，把v撤销掉，算完后反撤销，也就是再加回来，再dfs子树

复杂度

代码

#include
//#include
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair P;
#define fi first
#define se second
#define dbg(x) cerr<<(#x)<<":"<e[N];
void add(int &x,int y){
    x=(x+y)%mod;
}
int modpow(int x,int n,int mod){
    int res=1;
    for(;n;n>>=1,x=1ll*x*x%mod){
        if(n&1)res=1ll*res*x%mod;
    }
    return res;
}
void dfs(int u,int fa){
    sz[u]=1;
    h[u]=1;
    for(auto &v:e[u]){
        if(v==fa)continue;
        dfs(v,u);
        son[u]++;
        sz[u]+=sz[v];
        h[u]=1ll*h[u]*h[v]%mod;
    }
    h[u]=1ll*h[u]*fac[son[u]]%mod;
    //printf("u:%d son:%d h:%d\n",u,son[u],h[u]);
}
void dfs2(int u,int fa){
    int m=son[u];
    vector>f(m+1,vector(sz[u]+1,0));
    f[0][0]=1;//f[i][j]:选了i个节点 大小为j的方案数
    for(auto &v:e[u]){
        per(i,m,1){
            per(j,sz[u],sz[v]){
                add(f[i][j],f[i-1][j-sz[v]]);
            }
        }
    }
    h[u]=1ll*h[u]*modpow(fac[m],mod-2,mod)%mod;
    for(auto &v:e[u]){
        if(v==fa)continue;
        h[u]=1ll*h[u]*modpow(h[v],mod-2,mod)%mod;
        rep(i,1,m){
            rep(j,sz[v],sz[u]){
                add(f[i][j],mod-f[i-1][j-sz[v]]);
            }
        }
        vectorg(n+1,0);//g[k]:u、v距离为k的方案数
        rep(i,0,m-1){
            rep(j,0,sz[u]-1){
                add(g[j+1],1ll*f[i][j]*fac[i]%mod*fac[m-1-i]%mod*h[u]%mod);
            }
        }
        rep(i,0,n){
            if(!dp[u][i])continue;
            rep(j,1,sz[u]){
                if(!g[j])continue;
                add(dp[v][i+j],1ll*dp[u][i]*g[j]%mod);
            }
        }
        per(i,m,1){
            per(j,sz[u],sz[v]){
                add(f[i][j],f[i-1][j-sz[v]]);
            }
        }
        h[u]=1ll*h[u]*h[v]%mod;
        dfs2(v,u);
    }
    h[u]=1ll*h[u]*fac[m]%mod;
}
int main(){
    //freopen("jinan.in","r",stdin);
    //freopen("jinan.out","w",stdout);
    fac[0]=1;
    rep(i,1,M)fac[i]=1ll*fac[i-1]*i%mod;
    sci(n);
    rep(i,1,n-1){
        sci(u),sci(v);
        e[u].pb(v);
        e[v].pb(u);
    }
    dfs(1,0);
    dp[1][0]=1;
    dfs2(1,0);
    rep(i,1,n){
        rep(j,0,n-1){
            int ans=1ll*dp[i][j]*h[i]%mod;
            printf("%d%c",ans," \n"[j==n-1]);
        }
    }
    return 0;
}