算法导论——红黑树

红黑树是二叉搜索树的一种特例，它对每个节点增加了一个颜色的属性，通过增加以下的条件使得这颗二叉树更加平衡：
1.每个节点或是红色的，或是黑色的。
2.根节点是黑色的。
3.每个叶节点是黑色的。
4.如果一个节点是红色的，那么它的两个子节点都是黑色的。
5.对每个节点，从该节点到其所有后代节点的简单路径上，均包含相同数目的黑色节点。
红黑树的插入和删除如果按照二叉树的处理，那么它的性质可能被破坏，那么这个时候需要适当地去调整。

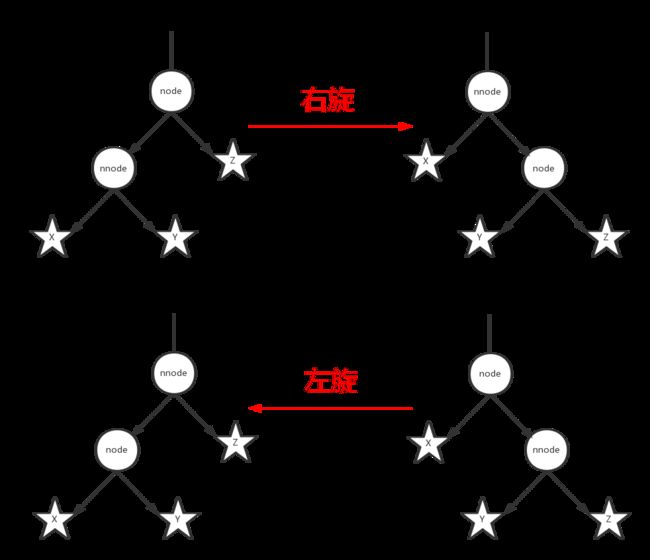
首先实现一下红黑树中需要用到的操作，左旋与右旋。这里左旋与右旋都是不改变二叉树的性质的。

C++实现如下：

void BRTree::left_rotate(Node *node){
    Node *nnode = node->right_child;

    node->right_child = nnode->left_child;
    if(nnode->left_child != nil)
        nnode->left_child->parent = node;
    nnode->parent = node->parent;

    if(node->parent == nil)
        root = nnode;
    else if(node == node->parent->left_child)
        node->parent->left_child = nnode;
    else
        node->parent->right_child = nnode;
    nnode->left_child = node;
    node->parent = nnode;
}

void BRTree::right_rotate(Node *node){
    Node *nnode = node->left_child;

    node->left_child = nnode->right_child;
    if(nnode->right_child != nil)
        nnode->right_child->parent = node;
    nnode->parent = node->parent;

    if(node->parent == nil)
        root = nnode;
    else if(node == node->parent->left_child)
        node->parent->left_child = nnode;
    else
        node->parent->right_child = nnode;
    nnode->right_child = node;
    node->parent = nnode;
}

红黑树节点的插入

首先按照正常的二叉树的插入。然后我们考虑到还需要维护的是红黑树的性质，那么我们就要考虑到插入的节点的颜色问题了。如果我们将这个节点涂成黑色，那么违背了性质5，但是很明显这个违背的性质涉及到这颗树中太多的路径了，其修改的成本太高。那么我们考虑将其涂成红色。那么这种情况下可能会违背两个性质，但是每次的违背都只违背其中的一个。那就是性质2,（这个时候刚好插入的根节点），性质4（这个时候节点的父节点是有可能是红色的）。由于这种违背涉及到的路径比较少，所以我们首先将插入的节点涂成红色，然后考虑后面的处理。

现在来调整一下红黑树使得它满足红黑树的性质。现在根据前面的分析，操作的当前节点是红色的。如果是违背了性质2那么直接将根节点染成黑色的就行了。如果违背的是性质4，那么此时父节点是红色的，现在就来讨论这种情况。只考虑当前节点的父节点是祖父节点的左子节点时的情况，右子节点时的情况与此对称。

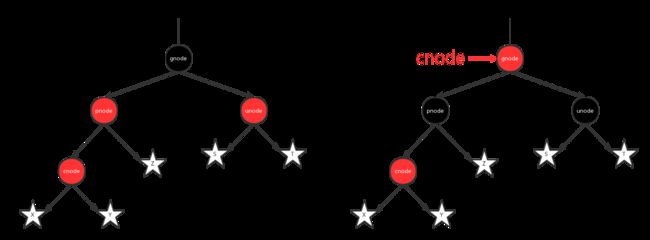
1.叔节点是红色：处理是将父节点和叔节点染成黑色，然后祖父节点染成红色，然后指定祖父节点，接续递归。

2.叔节点是黑色

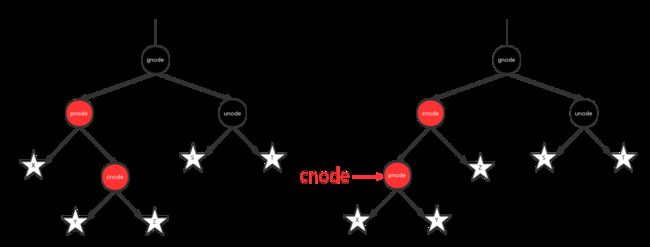
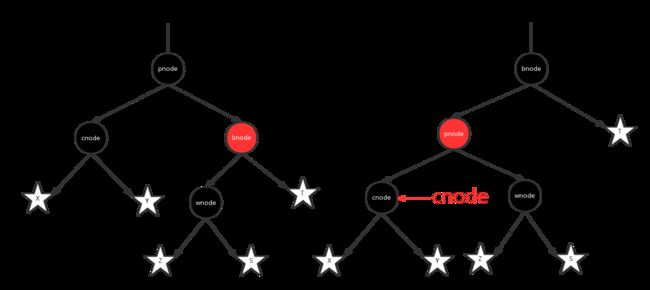
2.1.当前节点是父节点的右子节点：这个时候对父节点进行一次右旋操作，然后指定父节点为当前节点，就将情况转化为2.2

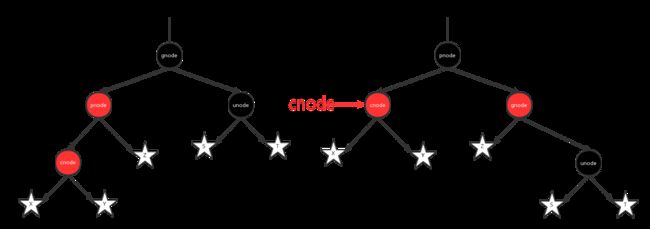
2.2当前节点是父节点的左子节点：对祖父节点进行一次右旋，然后祖父节点染成红色，父节点染成黑色，当前节点保持不变。

完成上面的操作之后，情况2达到了结束的条件，情况1将以新的当前节点继续递归。总结一下：上面的三种情况已经把所有的情况都考虑进去了。而每次操作之后性质1,3,5都是保持不变的，而满足性质4是递归结束的条件。那么剩下的只有可能是性质2不满足了。这个时候我们直接将根节点无条件染成黑色就行了。

红黑树节点的删除

首先像普通的二叉树一样删掉节点，这个过程用删掉节点的某个子节点或者是其后驱来替换删掉的节点。接着就是维护红黑树的性质了：如果删掉的节点不是拥有两个子节点，那么将由删掉的子节点来接替删掉的节点的位置，那么这种情况下可能破坏性质2和性质5。如果删掉的是根节点（黑色），并且替换的节点是红色的，那么违背了性质2需要进行调整。如果不是根节点，那么删掉的节点是红色的，那么没有违背性质，如果是黑色的，那么违背了性质5，这种情况下，以替代的节点为根的子树中的每条路径的黑色节点都比其他的路径少一个，这个时候假设这个替代节点有两重黑色就是满足条件的了，所以这个需要进行调整。如果删掉的节点拥有两个子节点，那么这个时候用删掉的节点的后驱的右子树来替换掉后驱节点，然后后驱节点替换掉删掉的节点就行了。下面讨论一下红黑树的性质的维护的问题。如果这个时候我们后驱节点的颜色不变，那么这个时候从后驱到之前后驱的右子节点之间的节点之间的黑色节点个数与删掉的节点和后驱节点的颜色都是相关的。我们为了使得变化最小化。我们将后驱节点的颜色染成跟删掉的节点一样，那么我们分析之后，后驱节点之前的右子树的性质受到了影响，因为这棵子树在路径上失去了一个节点（后驱节点，而且这个时候就相当于删掉了后驱节点，所以这种情况下在实现的时候记录的是后驱节点的颜色），具体的可能是性质5，而且这个是在删掉的后驱节点是黑色的情况下违背了性质5，这种情况下，以替代的节点为根的子树中的每条路径的黑色节点都比其他的路径少一个，这个时候假设这个替代节点有两重黑色就是满足条件的了，所以这个需要进行调整。

最后总结一下情况：我们在删掉的节点有两个子节点，用后驱节点替换删掉节点的情况下，我们现在将后驱节点当做删掉的节点分析（这种是等价的）：对应上面分析的三种情况都是当删掉的是黑色的时候需要调整，具体的方法是进行一定的变化，到当前节点是红色的时候，将这个节点涂成黑色，那么就解决了这棵子树的每条路径都少一个黑色节点的问题，如果当前节点是根节点，那更好办了，所有的路径已经都是一样的黑色节点数了，那就直接结束了。还是分情况进行讨论：

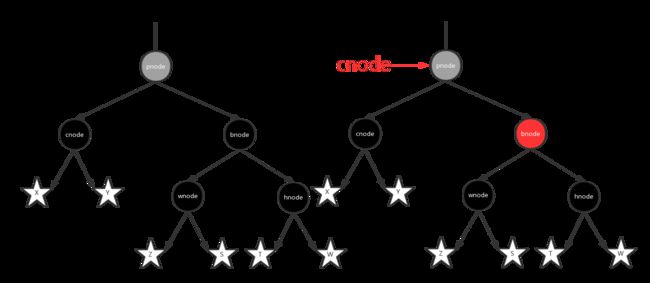
1.兄弟节点是红色：父节点染成红色，兄弟节点染成黑色，对父节点进行一次左旋，转化成情况2中的一种。

2.兄弟节点是黑色

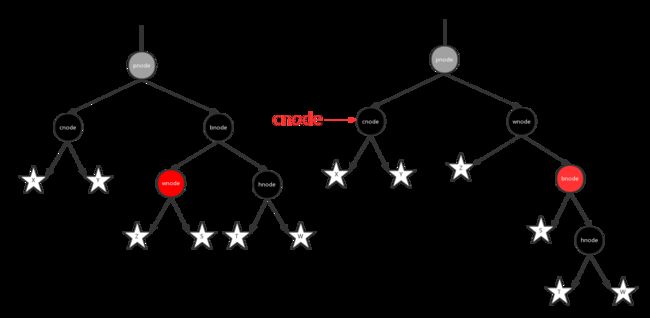
2.1.兄弟节点的两个子节点都是黑色：将兄弟节点染成红色，然后指定父节点为当前节点，继续迭代。

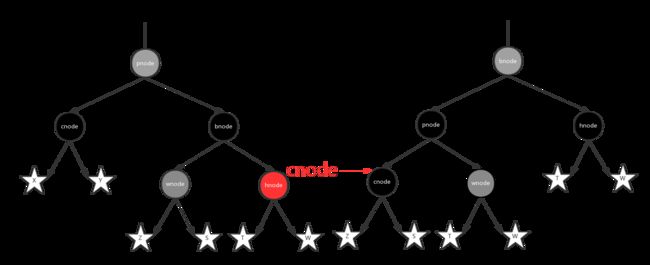
2.2.兄弟节点的左子节点是红色，右子节点是黑色：将兄弟节点的左子节点染成黑色，兄弟节点染成红色，对兄弟节点进行一次右旋转换成情况2.3。

2.3.兄弟节点的右子节点时红色：对父节点进行一次左旋，将兄弟节点的右子节点染成黑色，父节点染成黑色，兄弟节点染成父节点原来的颜色。，这个时候发现其实其他路径没有什么影响，但是当期节点所在的路径确实多了一个黑色的节点，这个时候其实是满足了条件，可以迭代结束了。

总结一下：所有的情况分为上面的几种，情况1可以转化为情况2中的一种，情况2.1会将当前节点向上移动，继续后面的迭代。情况2.2转化为情况2.3，情况2.3经过变化可以看出当前节点下的路径最后达到了我们期待的效果：黑色节点增加了一个，所以直接将root赋值给当前节点，迭代结束。

下面看一下红黑树的C++的实现

插入部分：

void BRTree::insert_fix(Node *node){
    Node *cnode = node;

    while(cnode->parent->color == RED){
        if(cnode->parent == cnode->parent->parent->left_child){
            Node *unode = cnode->parent->parent->right_child;
            Node *pnode = cnode->parent;
            Node *gnode = cnode->parent->parent;
            if(unode->color == RED){
                pnode->color = BLACK;
                unode->color = BLACK;
                gnode->color = RED;
                cnode = gnode;
            } else if(cnode == pnode->right_child){
                cnode = pnode;
                left_rotate(pnode);
            } else{
                pnode->color = BLACK;
                gnode->color = RED;
                right_rotate(gnode);
            }
        } else{
            Node *unode = cnode->parent->parent->left_child;
            Node *pnode = cnode->parent;
            Node *gnode = cnode->parent->parent;
            if(unode->color == RED){
                pnode->color = BLACK;
                unode->color = BLACK;
                gnode->color = RED;
                cnode = gnode;
            } else if(cnode == pnode->left_child){
                cnode = pnode;
                right_rotate(pnode);
            } else{
                pnode->color = BLACK;
                gnode->color = RED;
                left_rotate(gnode);
            }
        }
    }

    root->color = BLACK;
}

void BRTree::insert_tree(int t_value){
    Node *cur_parent = nil;
    Node *cur = root;
    Node *inode = new Node(t_value, RED, nil, nil, nil);

    while(cur != nil){
        cur_parent = cur;
        if(t_value < cur->value){
            cur = cur->left_child;
        } else{
            cur = cur->right_child;
        }

    }

    inode->parent = cur_parent;

    if(cur_parent == nil){
        root = inode;
    } else if(t_value < cur_parent->value){
        cur_parent->left_child = inode;
    } else{
        cur_parent->right_child = inode;
    }

    insert_fix(inode);
}

删除部分：

Node *BRTree::maximum_node(Node* node){
    Node *cnode = node;

    while(cnode->right_child != nil)
        cnode = cnode->right_child;

    return cnode;
}

void BRTree::transplant(Node *ori_node, Node *new_node){
    if(ori_node->parent == nil)
        root = new_node;
    else if(ori_node == ori_node->parent->left_child)
        ori_node->parent->left_child = new_node;
    else
        ori_node->parent->right_child = new_node;

    new_node->parent = ori_node->parent;
}

void BRTree::delete_fix(Node *node){
    Node *cnode = node;

    while(cnode != root && cnode->color == BLACK){
        Node *pnode = cnode->parent;
        if(cnode == pnode->left_child){
            Node *bnode = pnode->right_child;
            Node *wnode = bnode->left_child;
            Node *hnode = bnode->right_child;

            if(bnode->color == RED){
                pnode->color = RED;
                bnode->color = BLACK;
                left_rotate(pnode);
            } else if(wnode->color == BLACK && hnode->color == BLACK){
                bnode->color = RED;
                cnode = pnode;
            } else if(hnode->color == BLACK){
                bnode->color = RED;
                wnode->color = BLACK;
                right_rotate(bnode);
            } else {
                bnode->color = pnode->color;
                pnode->color = BLACK;
                hnode->color = BLACK;
                left_rotate(pnode);
                cnode = root;
            }
        } else{
            Node *bnode = pnode->left_child;
            Node *wnode = bnode->right_child;
            Node *hnode = bnode->left_child;

            if(bnode->color == RED){
                pnode->color = RED;
                bnode->color = BLACK;
                right_rotate(pnode);
            } else if(wnode->color == BLACK && hnode->color == BLACK){
                bnode->color = RED;
                cnode = pnode;
            } else if(hnode->color == BLACK){
                bnode->color = RED;
                wnode->color = BLACK;
                left_rotate(bnode);
            } else {
                bnode->color = pnode->color;
                pnode->color = BLACK;
                hnode->color = BLACK;
                right_rotate(pnode);
                cnode = root;
            }
        }
    }

    cnode->color = BLACK;
}

Node *BRTree::search_node(Node *node, int t_value){
    if(node == nil)
        return nil;

    if(t_value == node->value)
        return node;
    else if(t_value < node->value)
        return search_node(node->left_child, t_value);
    else
        return search_node(node->right_child, t_value);
}

void BRTree::delete_tree(int t_value){
    Node *dnode = search_node(root, t_value);
    Node *fnode;

    if(dnode == nil)
        return;

    Node *rdnode;
    Color rdcolor;

    if(dnode->left_child == nil){
        rdnode = dnode;
        rdcolor = rdnode->color;
        fnode = rdnode->right_child;

        transplant(rdnode, fnode);
    } else if(dnode->right_child == nil){
        rdnode = dnode;
        rdcolor = rdnode->color;
        fnode = rdnode->left_child;

        transplant(rdnode, fnode);
    } else{
        rdnode = maximum_node(dnode);
        rdcolor = rdnode->color;
        fnode = rdnode->right_child;

        transplant(rdnode, fnode);

        rdnode->right_child = dnode->right_child;
        dnode->right_child->parent = rdnode;
        rdnode->left_child = dnode->left_child;
        dnode->left_child->parent = rdnode;
        rdnode->color = dnode->color;

        transplant(dnode, rdnode);
    }

    if(rdcolor == BLACK)
        delete_fix(fnode);
}

总结一下：上面的过程针对红黑树插入和删除，为了维护好红黑树的性质，考虑到所有的情况，然后针对每种情况进行了处理。但是实现步骤是比较复杂的，其原理以及每次分类后操作的目的根本就不是很明确，纯碎靠死记硬背是可以记下来，但是实际上每个操作都是有其目的性的，后面将写专门的文章来讲述这其中的原理。