C语言每日一题（24）回文素数题解

BC158 [NOIP1999]回文数

题目描述

若一个数（首位不为零）从左向右读与从右向左读都一样，我们就将其称之为回文数。

例如：给定一个10进制数56，将56加65（即把56从右向左读），得到121是一个回文数。

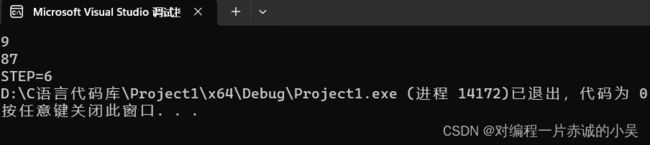
又如：对于10进制数87：

STEP1：87+78  = 165                  STEP2：165+561 = 726

STEP3：726+627 = 1353                STEP4：1353+3531 = 4884

在这里的一步是指进行了一次N进制的加法，上例最少用了4步得到回文数4884。

写一个程序，给定一个N（2<=N<=10或N=16）进制数M（100位之内），求最少经过几步可以得到回文数。如果在30步以内（包含30步）不可能得到回文数，则输出“Impossible!”

进制N>10时，使用大写'A'字母表示10，'B'表示11,...,'E'表示15

思路分析

本题是一道竞赛题，但实现思路比较简单，难就难在如何将它们联系在一起。

我们需要明确所需要实现的功能：

1.判断是否是回文数

2.如何实现n进制数的相加求和。

第一个功能，只需要将所给数存入数组，从左往右遍历，如果等于从右往左的值就是一个回文数。

其实也可以用求余运算判断，但这里考虑到16进制数，用一个字符数组存放会更加方便提取。

int is_hui(char* m, int sz)
{
	for (int i = 0; i < sz; i++)
	{
		if (m[i] != m[sz - i - 1]) return 0;//逆向思维，只要有一个不等就不是回文数
	}
	return 1;
}

重点在于第二个功能。

我能想到的思路就是将所给n进制数转换为10进制后进行相加，再将和转换为n进制进行判断。 

1.n进制转10进制

具体方法：从所输入的字符数组右往左提取每一个值，通过减去字符0的方法得到对应字符的整型，乘以它们对应位置的权值，权值的计算就是n在该位置的次方（pow（n，len-i-1)）（可以去看看n进制于十进制之间转换的方法，加深理解），再将值累加到所定义的sum里面。

特殊情况：

当n=10时，从左往右取每一个值与sum的10倍相加后再累加到sum里面。

当n=16同时该位置的值>=A，那就减去字符A再加上10即可取得对应的十进制数。

long long int todecrimal(char* m, int sz, int n)//题目要求，防止数据溢出，用ll类型
{
	long long int sum = 0;
	if (n == 10)
	{
		for (int i = 0; i < sz; i++)
		{
			int r = m[i] - '0';
			sum = sum * 10 + r;
		}
	}
	else
	{
		for (int j = sz - 1; j >= 0; j--)
		{
			int r = 0;
			if (n == 16 && m[j] >= 'A')
			{
				 r = m[j] - 'A' + 10;
			}
			else
			{
				r = m[j] - '0';
			}
			int tmp = r * pow(n, sz - j - 1);
			sum += tmp;
		}
	}
	return sum;
}

2.10进制转n进制

思路就是将所得的值（sum）取模运算拿到每一位的值，对n进行求余整除（基于十进制转n进制的方法）， 加上字符0完成整型到字符型的转换，放到字符数组里。

完成后还得将字符逆序才是正确的结果。

如果n=16且余数>=10，则加上字符A-10才是字符结果。

void backdecrimal(char* m, long long int sum,int n) void类型，不需要返回值
{
	int i = 0;
	while (sum)
	{
		if (n == 16 && (sum % n) >= 10)
		{
			m[i] = (sum % n) + 'A' - 10;
		}
		else
		{
			m[i] = (sum % n) + '0';
		}
		sum /= n;记得整除
		i++;
	}
	int x = 0;
	int y = i - 1;
	while (x < y)交换，逆序存放。
	{
		char tmp = m[x];
		m[x] = m[y];
		m[y] = tmp;
		x++;
		y--;
	}
	
}

 将上面两个函数整合一下，实现第二个功能

void addhui(int n, int sz, char* m)
{
	char mm[103] = { 0 };
	for (int i = 0; i < sz; i++)
	{
		mm[i] = m[sz - i - 1];//先将m数组逆序存放到另外一个数组里，方便后面相加
	}
	long long int sum = todecrimal(m, sz, n) + todecrimal(mm, sz, n);正序加逆序
	backdecrimal(m, sum, n);转换为n进制数放到m里面
}

完整代码

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include

int is_hui(char* m, int sz)
{
	for (int i = 0; i < sz; i++)
	{
		if (m[i] != m[sz - i - 1]) return 0;
	}
	return 1;
}
long long int todecrimal(char* m, int sz, int n)
{
	long long int sum = 0;
	if (n == 10)
	{
		for (int i = 0; i < sz; i++)
		{
			int r = m[i] - '0';
			sum = sum * 10 + r;
		}
	}
	else
	{
		for (int j = sz - 1; j >= 0; j--)
		{
			int r = 0;
			if (n == 16 && m[j] >= 'A')
			{
				 r = m[j] - 'A' + 10;
			}
			else
			{
				r = m[j] - '0';
			}
			int tmp = r * pow(n, sz - j - 1);
			sum += tmp;
		}
	}
	return sum;
}
void backdecrimal(char* m, long long int sum,int n)
{
	int i = 0;
	while (sum)
	{
		if (n == 16 && (sum % n) >= 10)
		{
			m[i] = (sum % n) + 'A' - 10;
		}
		else
		{
			m[i] = (sum % n) + '0';
		}
		sum /= n;
		i++;
	}
	int x = 0;
	int y = i - 1;
	while (x < y)
	{
		char tmp = m[x];
		m[x] = m[y];
		m[y] = tmp;
		x++;
		y--;
	}
	
}

void addhui(int n, int sz, char* m)
{
	char mm[103] = { 0 };
	for (int i = 0; i < sz; i++)
	{
		mm[i] = m[sz - i - 1];
	}
	long long int sum = todecrimal(m, sz, n) + todecrimal(mm, sz, n);
	backdecrimal(m, sum, n);
}




int main()
{
	int n = 0;
	char m[103] = { 0 };
	scanf("%d", &n);
	scanf("%s", m);
	int sz = strlen(m);
	int step = 0;
	while (sz = (int)strlen(m), is_hui(m, sz) == 0)//如果等于1跳出循环，计算step的值
	{
		step++;
		if (step >= 30) break;
		addhui(n, sz, m);
	}
	if (step < 30) printf("STEP=%d", step);
	else printf("Impossible!");
	return 0;
}