多密钥TFHE学习笔记1-MKTFHE的整体流程
多密钥TFHE学习笔记1-MKTFHE的整体流程
- MK-TFHE 的整体流程图
- TFHE 的多密钥变体的关键步骤
-
- 1. 设置 - MKHE.Setup( 1 λ 1^{\lambda} 1λ )
- 2. 密钥生成 - MKHE.KeyGen()
- 3. 加密 - MKHE.Enc( m m m )
- 4. 解密 - MKHE.Dec( c t ‾ , { s i } i ∈ [ k ] \overline{ct}, \{ \pmb{s}_i \} _{i \in [k]} ct,{sssi}i∈[k] )
- 5. 与非门运算 - MKHE.NAND( c t 1 ‾ , c t 2 ‾ , { ( P K i , B K i , K S i ) } i ∈ [ k ] \overline{ct_1}, \overline{ct_2}, \{ (PK_i, BK_i, KS_i) \}_{i \in [k]} ct1,ct2,{(PKi,BKi,KSi)}i∈[k] )
MK-TFHE 的整体流程图
MK-TFHE的整体流程从用户与服务器的角度看大致如下所示:
- 首先生成公共参数 CRS,将参数发送给每个参与方以及服务器(如果CRS生成不在服务器)
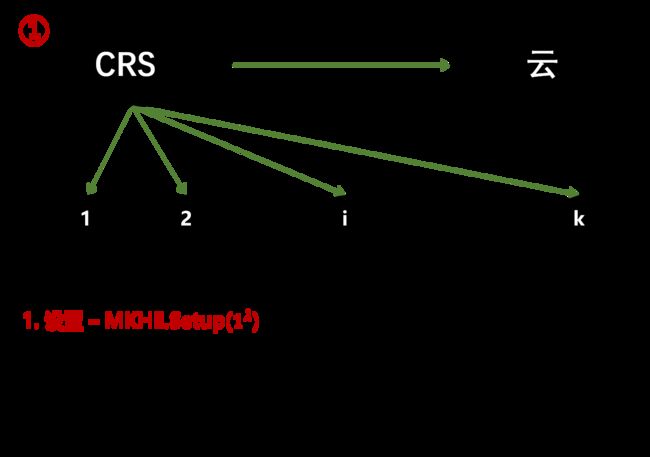
- 每个参与方独立地生成自己的密钥并加密消息,发送至服务器

- 服务器进行同台评估过程,将结果返回给参与方

- (在联合解密中)所有参与计算的参与方共同解密密文,得到结果

TFHE 的多密钥变体的关键步骤
首先做一些约定:
- 除非特殊说明,否则算法以 2 为底数。
- 向量使用加粗的字体表示,矩阵使用加粗大写的字体表示。
- 内积使用 < ⋅ , ⋅ > < \sdot , \sdot> <⋅,⋅> 表示。
- 对于实数 r r r ,使用 ⌊ r ⌉ \lfloor r \rceil ⌊r⌉ 表示取整(取距离 r r r 最近的整数,相等时向上舍入)。
- 使用 x ← D x \leftarrow D x←D 表示从分布 D D D 中取样 (sample) x x x 。
- 对于有限集合 S S S ,使用 U ( S ) U(S) U(S) 表示集合 S S S 上的均匀分布。
- 使用 D α D_{\alpha} Dα 表示方差为 α 2 \alpha^{2} α2 的高斯分布。
- 使用 λ \lambda λ 表示安全参数。
- 所有已知的对该密码方案的攻击需要 Ω ( 2 λ ) \Omega(2^{\lambda}) Ω(2λ) 比特的操作。
- 对于正整数 k k k ,使用 [ k ] [k] [k] 表示其索引集合 { 1 , 2 , . . . , k } \{1, 2, ... ,k\} {1,2,...,k} 。
以下为多密钥 TFHE (MKTFHE) 的重要步骤:
1. 设置 - MKHE.Setup( 1 λ 1^{\lambda} 1λ )
- 调用 LWE.Setup ( 1 λ 1^\lambda 1λ ) 来生成 LWE 的参数 p p L W E = ( n , χ , α , B ′ , d ′ ) pp^{LWE} = (n, \chi, \alpha, B', d') ppLWE=(n,χ,α,B′,d′) 。其中 n n n 为 LWE 的维度, χ \chi χ 为 LWE 密钥的分布, α \alpha α 为错误率, B ′ B' B′ 为分解基, d ′ d' d′ 为密钥转换 gadget 向量的维度。密钥转换 gadget 向量: g ′ = ( B ′ − 1 , . . . , B ′ − d ′ ) g' = (B'^{-1}, ... , B'^{-d'}) g′=(B′−1,...,B′−d′) 。
- 调用 RLWE.Setup ( 1 λ 1^\lambda 1λ ) 来生成 RLWE 的参数 p p R L W E = ( N , ψ , β , B , d , a ) pp^{RLWE} = (N, \psi, \beta, B, d,\pmb{a}) ppRLWE=(N,ψ,β,B,d,aaa) 。其中 N N N 为 RLWE 的维度(2的幂), ψ \psi ψ 为 RLWE 密钥在 R R R 上的分布,并且错误率为 α \alpha α , B ≥ 2 B \geq 2 B≥2 是整数基,分解维度为 d d d , gadget 向量为 g = ( B − 1 , . . . , B − d ) g = (B^{-1}, ... , B^{-d}) g=(B−1,...,B−d) 。 a \pmb{a} aaa 为分布 T d T^d Td 上的均匀分布的采样。
- 返回生成的公共参数 p p M K H E = ( p p L W E , p p R L W E ) pp^{MKHE} = (pp^{LWE}, pp^{RLWE}) ppMKHE=(ppLWE,ppRLWE) 。
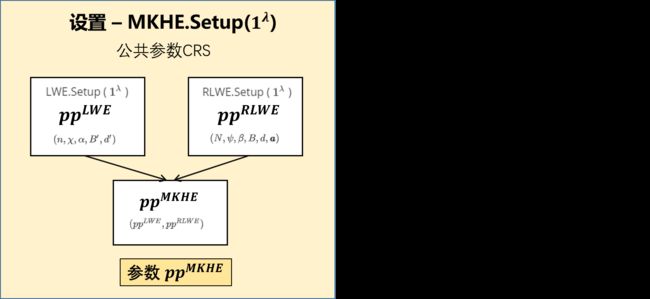
*假设 MKHE 的算法都默认将 p p M K H E pp^{MKHE} ppMKHE 作为输入。公共参数为 CRS ,可以理解为是所有人都知道的信息。
2. 密钥生成 - MKHE.KeyGen()
- 生成 LWE 密钥 s i ← L W E . K e y G e n ( ) s_i \leftarrow LWE.KeyGen() si←LWE.KeyGen() 。这一步仅为从分布 χ \chi χ 中采样密钥。
- 运行 ( z i , b i ) ← R L W E . K e y G e n ( ) (z_i, \pmb{b}_i) \leftarrow RLWE.KeyGen() (zi,bbbi)←RLWE.KeyGen() 并且设置公钥为 P K i = b i PK_i = \pmb{b}_i PKi=bbbi 。从分布 ψ \psi ψ 中采样 z z z ,设 z = ( 1 , z ) \pmb{z} = (1, z) zzz=(1,z) 。从 D α d D_{\alpha}^d Dαd 中取一个误差向量 e \pmb{e} eee ,计算公钥 b = − z ⋅ a + e \pmb{b} = -z \sdot \pmb{a} + \pmb{e} bbb=−z⋅aaa+eee (mod 1) 。对于 z i = z 1 , 0 + z i , 1 X + . . . + z i , N − 1 X N − 1 z_i = z_{1,0} + z_{i,1}X + ... + z_{i,N-1}X^{N-1} zi=z1,0+zi,1X+...+zi,N−1XN−1 ,记 z i ∗ = ( z i , 0 , − z i , N − 1 , . . . , − z i , 1 ) ∈ Z N \pmb{z}_i^* = (z_{i,0},-z_{i,N-1}, ... , -z_{i,1}) \in \mathbb{Z}^N zzzi∗=(zi,0,−zi,N−1,...,−zi,1)∈ZN 。
- 对于 j ∈ [ n ] j \in [n] j∈[n] ,生成 ( d i , j , F i , j ) ← R L W E . U n i E n c ( s i , j , z i ) (\pmb{d}_{i,j}, \pmb{F}_{i,j}) \leftarrow RLWE.UniEnc(s_{i,j},z_i) (dddi,j,FFFi,j)←RLWE.UniEnc(si,j,zi) ,即使用 RLWE 密钥加密 LWE 密钥。同时,设置自举密钥为 B K i = { ( d i , j , F i , j ) } j ∈ [ n ] BK_i = \{ (\pmb{d}_{i,j}, \pmb{F}_{i,j}) \}_{j \in [n]} BKi={(dddi,j,FFFi,j)}j∈[n] 。从 ψ \psi ψ 中取一个随机值 r r r ,可将 d \pmb{d} ddd 看作是随机值 r r r 加密下的 LWE 密钥 s s s ,将 F \pmb{F} FFF 看成是 RLWE 密钥 z z z 加密下的随机值 r r r 。
- 生成密钥转换密钥 K S ← L W E . K S G e n ( z i ∗ , s i ) KS \leftarrow LWE.KSGen(\pmb{z}_i^*, \pmb{s}_i) KS←LWE.KSGen(zzzi∗,sssi) ,能够将一个与 t ∈ Z N \pmb{t} \in \mathbb{Z}^N ttt∈ZN 对应的 LWE 密文转换为同一消息在 s ∈ Z n \pmb{s} \in \mathbb{Z}^n sss∈Zn 加密下的另一个 LWE 密文。
- 返回密钥 s i \pmb{s}_i sssi ,公开密钥的三元组 ( P K i , B K i , K S i ) (PK_i, BK_i, KS_i) (PKi,BKi,KSi) ,分别为公钥、自举密钥、密钥转换密钥。

*每个参与方都独立进行该步骤,下标 i i i 表示第 i i i 个参与方。
*注意对于任意 a = a 0 + a 1 X + . . . + a N − 1 X N − 1 ∈ T a = a_0 + a_1X + ... + a_{N-1}X^{N-1} \in T a=a0+a1X+...+aN−1XN−1∈T 和它的系数构成的向量 ( a 0 , . . . , a N − 1 ) ∈ T N (a_0, ... , a_{N-1}) \in \mathbb{T}^N (a0,...,aN−1)∈TN , a ⋅ z ∈ T a \sdot z \in T a⋅z∈T 的常数项等价于 < a , z ⋆ > < \pmb{a}, \pmb{z}^{\star}> <aaa,zzz⋆> 模 1 ,其中 T = T [ X ] / ( X N + 1 ) T = \mathbb{T} [X] / (X^N + 1) T=T[X]/(XN+1) 。
3. 加密 - MKHE.Enc( m m m )
对于输入比特 m ∈ { 0 , 1 } m \in \{ 0, 1 \} m∈{0,1} ,运行 L W E . E n c ( m ) LWE.Enc(m) LWE.Enc(m) 并返回一个 LWE 密文,其中 scaling factor = 1 4 \frac{1}{4} 41 (与 FHEW/TFHE 方案中意义相同)。这是一个标准的 LWE 加密,从 T n \mathbb{T}^n Tn 中均匀采样得到 a \pmb{a} aaa 作为 mask ,从 D α D_{\alpha} Dα 中采样得到 e e e 作为误差。输出密文 c t = ( b , a ) ∈ T n + 1 ct = (b, \pmb{a}) \in \mathbb{T}^{n+1} ct=(b,aaa)∈Tn+1 满足 b + < a , s > ≈ 1 4 m ( m o d 1 ) b + < \pmb{a} , \pmb{s} > \approx \frac{1}{4}m \quad (mod 1) b+<aaa,sss>≈41m(mod1) 。

*同态计算后密文的维度增加,应存储参与方的索引以便解密和进行同态操作。
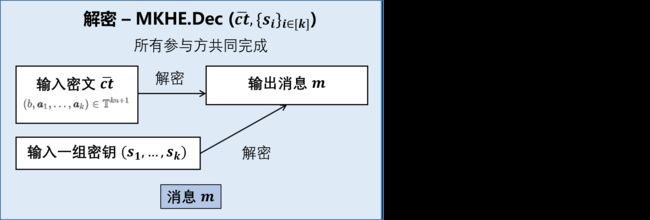
4. 解密 - MKHE.Dec( c t ‾ , { s i } i ∈ [ k ] \overline{ct}, \{ \pmb{s}_i \} _{i \in [k]} ct,{sssi}i∈[k] )
对于密文 c t ‾ = ( b , a 1 , . . . , a k ) ∈ T k n + 1 \overline{ct} = (b, \pmb{a}_1, ... , \pmb{a}_k) \in \mathbb{T}^{kn+1} ct=(b,aaa1,...,aaak)∈Tkn+1 和一组密钥 ( s 1 , . . . , s k ) (\pmb{s}_1, ..., \pmb{s}_k) (sss1,...,sssk) ,返回比特 m ∈ { 0 , 1 } m \in \{ 0, 1 \} m∈{0,1} 使得 ∣ b + ∑ i = 1 k < a i , s i > − 1 4 m ∣ |b + \sum_{i = 1}^{k} <\pmb{a}_i , \pmb{s}_i> - \frac{1}{4}m | ∣b+∑i=1k<aaai,sssi>−41m∣ 最小。
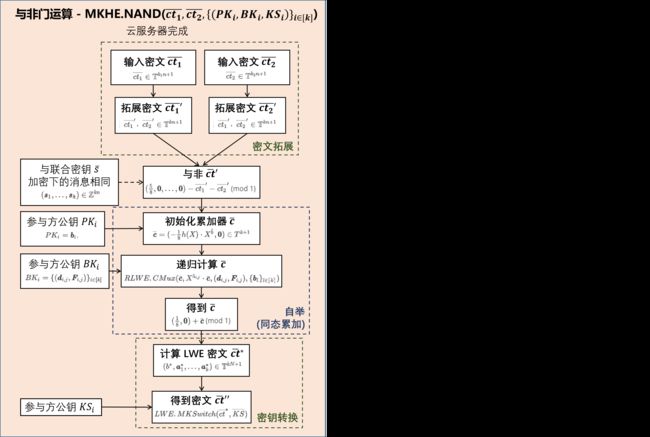
5. 与非门运算 - MKHE.NAND( c t 1 ‾ , c t 2 ‾ , { ( P K i , B K i , K S i ) } i ∈ [ k ] \overline{ct_1}, \overline{ct_2}, \{ (PK_i, BK_i, KS_i) \}_{i \in [k]} ct1,ct2,{(PKi,BKi,KSi)}i∈[k] )
给定两个 LWE 密文 c t 1 ‾ ∈ T k 1 n + 1 \overline{ct_1} \in \mathbb{T}^{k_1n+1} ct1∈Tk1n+1 和 c t 2 ‾ ∈ T k 2 n + 1 \overline{ct_2} \in \mathbb{T}^{k_2n+1} ct2∈Tk2n+1 ,令 k k k 为参与者的数量,与 c t 1 ‾ \overline{ct_1} ct1 或 c t 2 ‾ \overline{ct_2} ct2 相关。对于 i ∈ [ k ] i \in [k] i∈[k] , P K i = b i , B K i = { ( d i , j , F i , j ) } i ∈ [ k ] , K S i PK_i = \pmb{b}_i , BK_i = \{ (\pmb{d}_{i,j}, \pmb{F}_{i,j}) \}_{i \in [k]}, KS_i PKi=bbbi,BKi={(dddi,j,FFFi,j)}i∈[k],KSi 分别为第 j j j 个参与方的 公钥、自举密钥、密钥转换密钥。
- 拓展输入的 LWE 密文并且在密文比特上同态评估与非门 m = m 1 ⊼ m 2 m = m_1 \barwedge m_2 m=m1⊼m2 。
- 将密文 c t 1 ‾ \overline{ct_1} ct1 和 c t 2 ‾ \overline{ct_2} ct2 拓展至 c t 1 ‾ ′ , c t 2 ‾ ′ ∈ T k n + 1 \overline{ct_1}',\overline{ct_2}' \in \mathbb{T}^{kn + 1} ct1′,ct2′∈Tkn+1 :联合密钥 s ‾ = ( s 1 , . . . , s k ) ∈ Z k n \overline{\pmb{s}} = (\pmb{s}_1, ... , \pmb{s}_k) \in \mathbb{Z}^{kn} sss=(sss1,...,sssk)∈Zkn 加密下的相同消息。只需要重新排列并在空槽 (slots) 中放入 0 即可。
- 计算 c t ‾ ′ = ( 5 8 , 0 , . . . , 0 ) − c t 1 ‾ ′ − c t 2 ‾ ′ \overline{ct}' = (\frac{5}{8}, \pmb{0}, ... , \pmb{0}) - \overline{ct_1}' - \overline{ct_2}' ct′=(85,000,...,000)−ct1′−ct2′ (mod 1) 。这个是与非门的标志步骤。
- 同态累加 (homomorphic accumulator) :使用 RSGW 方案的外积来评估拓展 LWE 密文的解密电路,来实现自举。
- 初始化累加器 c ˉ \bar{\pmb{c}} cccˉ :令 c t ‾ ′ = ( b ′ , a 1 ′ , . . . , a k ′ ) ∈ T k n + 1 \overline{ct}' = (b', \pmb{a}_1', ... , \pmb{a}_k') \in \mathbb{T}^{kn+1} ct′=(b′,aaa1′,...,aaak′)∈Tkn+1 ,计算 b ~ = ⌊ 2 N ⋅ b ′ ⌉ \widetilde{b} = \lfloor 2N \sdot b' \rceil b =⌊2N⋅b′⌉ 和 a ~ i = ⌊ 2 N ⋅ a i ′ ⌉ \widetilde{\pmb{a}}_i = \lfloor 2N \sdot \pmb{a}_i' \rceil aaa i=⌊2N⋅aaai′⌉ 。初始化 RLWE 密文为 c ‾ = ( − 1 8 h ( X ) ⋅ X b ~ , 0 ) ∈ T k + 1 \overline{\pmb{c}} = (- \frac{1}{8}h(X) \sdot X ^{\tilde{b}},\pmb{0}) \in T^{k + 1} ccc=(−81h(X)⋅Xb~,000)∈Tk+1 其中 h = ∑ − N 2 < j < N 2 X j = 1 + X + . . . + X N 2 − 1 − X N 2 + 1 − . . . − X N − 1 h = \sum_{- \frac{N}{2} < j < \frac{N}{2}} X^j = 1 + X + ... + X^{\frac{N}{2}-1} - X^{\frac{N}{2} + 1} - ... - X^{N-1} h=∑−2N<j<2NXj=1+X+...+X2N−1−X2N+1−...−XN−1 。这是 − 1 8 h ( X ) ⋅ X b ~ - \frac{1}{8}h(X) \sdot X ^{\tilde{b}} −81h(X)⋅Xb~ 的平凡的 (trivial) RLWE 密文。
- 使用 Mux 门来实现主要的计算:对于 i ∈ [ k ] i \in [k] i∈[k] ,令 a ~ i = ( a ~ i , j ) j ∈ [ n ] \tilde{\pmb{a}}_i = (\tilde{a}_{i,j})_{j \in [n]} aaa~i=(a~i,j)j∈[n] 。对于 i ∈ [ k ] i \in [k] i∈[k] 和 j ∈ [ n ] j \in [n] j∈[n] ,递归地计算 c ˉ ← R L W E . C M u x ( c ˉ , X a ~ i , j ⋅ c ˉ , ( d i , j , F i , j ) , { b l } l ∈ ⌈ k ⌉ ) \bar{\pmb{c}} \leftarrow RLWE.CMux(\bar{\pmb{c}}, X^{\tilde{a}_{i,j}} \sdot \bar{\pmb{c}}, (\pmb{d}_{i,j}, \pmb{F}_{i,j}), \{ \pmb{b}_l \}_{l \in \lceil k \rceil}) cccˉ←RLWE.CMux(cccˉ,Xa~i,j⋅cccˉ,(dddi,j,FFFi,j),{bbbl}l∈⌈k⌉) 。
- 返回 c ˉ ← ( 1 8 , 0 ) + c ˉ \bar{\pmb{c}} \leftarrow (\frac{1}{8}, \pmb{0}) + \bar{\pmb{c}} cccˉ←(81,000)+cccˉ (mod 1) 。
- 将 c ‾ \overline{\pmb{c}} ccc 转换为 LWE 密文并运行多密钥的密钥转换算法。
- 对于 c ˉ = ( c 0 , c 1 , . . . , c k ) ∈ T k + 1 \bar{\pmb{c}} = (c_0, c_1, ... , c_k) \in T^{k + 1} cccˉ=(c0,c1,...,ck)∈Tk+1 ,令 b ∗ b^* b∗ 为 c 0 c_0 c0 的常数项,对于 i ∈ [ k ] i \in [k] i∈[k] ,令 a i ∗ \pmb{a}_i^* aaai∗ 为 c i c_i ci 的系数向量。计算 LWE 密文 c t ‾ ∗ = ( b ∗ , a 1 ∗ , . . . , a k ∗ ) ∈ T k N + 1 \overline{ct}^* = (b^*, \pmb{a}_1^*, ... , \pmb{a}_k^*) \in \mathbb{T}^{kN + 1} ct∗=(b∗,aaa1∗,...,aaak∗)∈TkN+1 。
- 令 K S ‾ = { K S i } i ∈ [ k ] \overline{KS} = \{ KS_i \}_{i \in [k]} KS={KSi}i∈[k] ,执行多密钥的密钥转换算法 (multi-key-switching) 并返回密文 c t ‾ ′ ′ ← L W E . M K S w i t c h ( c t ‾ ∗ , K S ‾ ) \overline{ct}'' \leftarrow LWE.MKSwitch(\overline{ct}^*, \overline{KS}) ct′′←LWE.MKSwitch(ct∗,KS) 。这个密钥转换算法输入拓展密文和一系列密钥转换密钥,返回相同消息在联合密钥加密下的密文。
主要参考论文:
- Chen H, Chillotti I, Song Y. Multi-key homomorphic encryption from TFHE[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Cham, 2019: 446-472.
网址:https://link.springer.com/chapter/10.1007/978-3-030-34621-8_16
算法库:https://github.com/ilachill/MK-TFHE