【Unity】浅谈UGUI的锚点和自适应
文章目录
-
- UGUI 锚点的使用
-
-
- Pivot点
- 锚点的初级使用
-
- 锚点的理解
-
-
- anchorMin,anchorMax
- sizeDelta
- anchoredPosition
- 推导与证明
-
- 总结
- 讨论
最近在做一个UGUI的Demo，我们知道要做自适应，绕不开RectTransform组件中锚点的设置。我先总结一下我的UGUI锚点的使用，最后重点说明一下自己对于锚点的理解，主要是回答以下问题：
- 如何理解UGUI的锚点
- 为什么不同的锚点设置，有时候能设置宽高，有时候不能
- 什么是anchoredPosition，sizeDelta
UGUI 锚点的使用
我们要先清楚Pivot的概念。
Pivot点
它用来表示一个RectTransform的中心点。当你试图改变一个物体的宽高的时候，比如直接代码里设置RectTransform.rect的值，或者RectTransform组件面板上允许设置宽高的值的时候，Pivot点决定了物体如何向两边延伸。
Pivot点的坐标是一个归一化的2D模型坐标系下的坐标，该坐标系原点（0，0）在当前UI的左下角，UI的右上角是(1，1)。比如Pivot点（0.4，0.8）表示当前UI的中心点在宽度40%和高度80%的位置。当你试图将物体的宽扩大 Δx时，Δx中有40%的部分被分配在了pivot的左边，剩下的部分被分配在了pivot点的右边。
当你需要动态扩展一个UI时，比如一个文本框，你希望文本框的宽度能够根据文本占据的像素动态扩展，同时此时文本是水平居左对齐，那你需要将pivot点设置在UI的左边框上，即pivot.x= 0，这样当文本框的宽度变大时，它只会向右扩展，而不是向两边扩展。
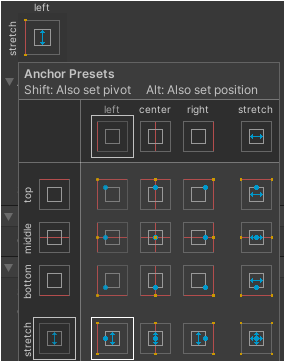
锚点的初级使用
锚点是父物体上的四个点，在RectTransform组件的这里可以快速设置锚点的位置。
锚点决定了当屏幕分辨率发生改变的时候，UI的位置和大小如何变化。在RectTransform面板上，设置锚点的右侧，能够设置四个值（PosZ一般没有什么用，不参与讨论），如下图：
我们需要注意一个事实，就是无论屏幕的分辨率发生怎样的变化，这里的值都不会发生改变，但是不同的锚点设置，这四个值表示的含义不一样。我们将锚点的使用分成了三种情况讨论，当屏幕分辨率发生改变的时候，你希望：
一，UI的位置相对父物体的一个点保持不变，宽高保持不变
此时你可以选择这九种锚点。这九种锚点有一个共同的特点，就是四个锚点的位置重合在了一起。
此时，面板的四个值有两个值表示pivot点相对于锚点的坐标（posX, posY），有两个值表示物体的宽和高。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UXEiFpeT-1608449689634)(1C137E67056B43129006F64EA0B3745C)]](http://img.e-com-net.com/image/info8/2f88bb523ef64f80aae98a062ce46166.jpg)
二，UI的四条边和父物体的对应四条边的距离保持不变，宽高根据上述条件自适应
此时你可以选择这种锚点。这种锚点的特点是四个锚点的位置各不相同。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dYW60ZHO-1608449689635)(BD8ED5EC5FE3403FA36871844CFD38FE)]](http://img.e-com-net.com/image/info8/09a1ef97d81c47e0b7cf797a871bfc8b.png){kind=small}
此时，面板的四个值分别表示物体的左边框距离父物体的左边框的距离，…，下边框距离父物体的下边框的距离。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7vyEolfL-1608449689636)(1AE049964BBB41AB85BEA156355482E4)]](http://img.e-com-net.com/image/info8/567bc461d27d4082a0d60829611a6e54.jpg)
三，UI的左右边框/上下边框距离父物体对应边框的距离保持不变，UI的高/宽保持不变
此时你可以选择剩下的六种锚点，这些锚点的特点是有两对内部两两位置重合的锚点。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VxZeoAqD-1608449689636)(4E3855EB31D441779812386F21E8713B)]](http://img.e-com-net.com/image/info8/0ca6af3bd6cc464b8bd44679cd621885.png){kind=small}
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zhwcQPux-1608449689636)(C00E090B07744101A126351946F71C5B)]](http://img.e-com-net.com/image/info8/33a6d80364a643dd8d55f0dfd04c79b8.png){kind=small}
这其实是第一种情况和第二种情况的组合。其中一个维度采用第一种情况的约束，另一个维度采用第二种情况的约束。比如，在宽度上保持不变，高度根据上下边框的约束自适应。此时面板的四个值，有两个值表示上下边框距离父物体对应边框的距离，另外两个，一个表示物体的宽度，一个表示物体pivot点相对于锚点的X坐标。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EmQSborK-1608449689637)(37F82DF7273844E0B5FF78FF2A50D53D)]](http://img.e-com-net.com/image/info8/878eee9423f84fa6b4f824d1bbef2741.jpg)
锚点的理解
很多网上的讲解都是像上面这样分情况解释的，包括解释sizeDelta的含义的时候，也是说这种情况等于Top和Bottom之和，另一种情况表示物体的高。但这终究只是一种表象，它内在的运算一定是统一的。
我们知道，无论你设置什么样的锚点，当屏幕分辨率发生变化的时候，UI的新的位置和大小只跟新的屏幕率有关。从这个事实我们可以推出一个结论，就是当屏幕分辨率发生变化的时候，RectTransform中一定有一些量是保持不变的，只有这样才能唯一确定在一个分辨率下UI的位置和大小。
现在我直接说结论，再证明。这些不变的量分别是：
- pivot 比例坐标
- anchorMin,anchorMax
- sizeDelta
- anchoredPosition
在证明之前，先说一下上面四个不变量的含义。pivot比例坐标已经讲过了，它是一个归一化的2D模型坐标系下坐标点。
anchorMin,anchorMax
这两个变量描述的是锚点的位置。我们除了使用上面Unity给出的三种情况的锚点之外，还可以自己手动指定四个锚点的位置。
由于一个对角线就可以确定一个水平四边形，所以我们只需要四个值就可以描述四个锚点位置。anchorMin描述了左下角锚点的坐标，anchorMax描述了右上角锚点的坐标。这个坐标是归一化的屏幕空间坐标系下的坐标，它的原点（0，0）在屏幕空间的左下角，右上角是（1，1）。这跟pivot相对坐标的定义很相似。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HVrtqEqy-1608449689638)(766058687237481FB95FB1F3600F2F2E)]](http://img.e-com-net.com/image/info8/fb5c1c5c5da34cab9393eebcd05b7091.jpg)
sizeDelta
sizeDelta在检视面板上不能直接看出来，我们可以打开面板的debug模式，就可以看到sizeDelta的值了。sizeDelta描述的是RectTransform的四个角相对于四个锚点的屏幕空间下的距离差。我们假设屏幕空间坐标系下，左下角的锚点坐标是（x1, y1），右上角锚点坐标（x2, y2），同时当前物体的RectTransform的左下角坐标（a1, b1），右上角（a2, b2），记sizeDelta值为（d1, d2）则
d 1 = a 1 − x 1 + x 2 − a 2 d 2 = b 1 − y 1 + y 2 − b 2 (1) d_1 = a_1 - x_1 + x_2 - a_2 \\ d_2 = b_1 - y_1 + y_2 - b_2\tag{1} d1=a1−x1+x2−a2d2=b1−y1+y2−b2(1)
anchoredPosition
anchoredPosition也需要打开面板的debug模式才可以在面板上查看这个值。这个值相对比较复杂。它描述的是屏幕空间坐标系下，当前物体的pivot点相对于锚点的pivot点的距离。锚点的pivot点是什么意思呢，其实，你可以把四个锚点看成是一个UI的四个角，锚点的pivot点就是这个UI的pivot点。那它的pivot比例坐标是多少呢？答案是等于当前物体的pivot比例坐标。换句话说，假设当前物体的pivot点在左边框的中心，那锚点的pivot点就是左侧两个锚点的中心。假设屏幕空间坐标系下物体的pivot点坐标为（pa, pb），锚点的pivot点坐标为（px，py）。
则
a n c h o r e d P o s i t i o n = ( p x − p a , p y − p b ) anchoredPosition = (p_x - p_a, p_y - p_b) anchoredPosition=(px−pa,py−pb)
我们可以设置不同的锚点，设置物体不同的pivot比例坐标，然后每次都将anchoredPosition设置成（0，0），验证一下上述结论。
推导与证明
有了上面的这些值之后，现在假设屏幕分辨率变了，我们只用上面这些值尝试重建UI的坐标和大小。
- 我们通过anchorMin, anchorMax确定新的分辨率下四个锚点的位置。
- 记pivot的比例坐标为（m1, m2），然后据此确定锚点的pivot点
- 根据锚点的pivot点和anchoredPosition确定UI的pivot点坐标，假设屏幕空间坐标系下新的pivot点坐标为（p1, p2）
- 之后我们根据sizeDelta的方程（1），以及pivot的比例坐标的定义，有方程组：
d 1 = a 1 − x 1 + x 2 − a 2 d 2 = b 1 − y 1 + y 2 − b 2 m 1 = a 1 − x 1 a 2 − a 1 m 2 = b 1 − y 1 b 2 − b 1 \begin{aligned} d_1 &= a_1 - x_1 + x_2 - a_2 \\ d_2 &= b_1 - y_1 + y_2 - b_2 \\ m_1 &= \frac{a_1 - x1}{a_2 - a_1}\\ m_2 &= \frac{b_1 - y1}{b_2 - b_1} \end{aligned} d1d2m1m2=a1−x1+x2−a2=b1−y1+y2−b2=a2−a1a1−x1=b2−b1b1−y1
求解上述方程组，得：
a 1 = x 1 + m 1 ⋅ ( x 2 − x 1 − d 1 ) a 2 = x 2 − d 1 + m 1 ⋅ ( x 2 − x 1 − d 1 ) b 1 = y 1 + m 2 ⋅ ( y 2 − y 1 − d 2 ) b 2 = y 2 − d 2 + m 2 ⋅ ( y 2 − y 1 − d 2 ) (2) \begin{aligned} a_1 &= x_1 + m_1\cdot(x_2 - x_1 - d_1)\\ a_2&= x_2 - d_1 + m_1\cdot(x_2 - x_1 - d_1)\\ b_1 &= y_1 + m_2\cdot(y_2 - y_1 - d_2)\\ b_2&= y_2 - d_2 + m_2\cdot(y_2 - y_1 - d_2)\tag{2} \end{aligned} a1a2b1b2=x1+m1⋅(x2−x1−d1)=x2−d1+m1⋅(x2−x1−d1)=y1+m2⋅(y2−y1−d2)=y2−d2+m2⋅(y2−y1−d2)(2)
这样，确定了UI的四个角的屏幕空间坐标之后我们就完成了新的屏幕分辨率下UI的重建。现在，我们来考虑一下，当x1 = x2，即上面一对和下面一对锚点分别重合的时候，会发生什么，此时，等式（2）退化成：
a 1 = x 1 − m 1 ⋅ d 1 a 2 = x 1 − d 1 − m 1 ⋅ d 1 b 1 = y 1 + m 2 ⋅ ( y 2 − y 1 − d 2 ) b 2 = y 2 − d 2 + m 2 ⋅ ( y 2 − y 1 − d 2 ) \begin{aligned} a_1 &= x_1 - m_1\cdot d_1\\ a_2&= x_1 - d_1 - m_1\cdot d_1\\ b_1 &= y_1 + m_2\cdot(y_2 - y_1 - d_2)\\ b_2&= y_2 - d_2 + m_2\cdot(y_2 - y_1 - d_2) \end{aligned} a1a2b1b2=x1−m1⋅d1=x1−d1−m1⋅d1=y1+m2⋅(y2−y1−d2)=y2−d2+m2⋅(y2−y1−d2)
此时：
a 2 − a 1 = w i d t h = − d 1 a_2 - a_1 = width = -d_1 a2−a1=width=−d1
即此时，在x2 = x1的情况下，UI的宽度变成了一个常量，其值等于sizeDelta的x坐标符号取反。这也就是为什么，在上面讨论锚点类型的时候，第三种情况下，不变的量会出现一个宽度。同理，当四个锚点都坍缩成一个点的时候：
a 2 − a 1 = w i d t h = − d 1 b 2 − b 1 = h e i g h t = − d 2 \begin{aligned} a_2 - a_1 &= width &= -d_1\\ b_2 - b_1 &= height &= -d_2 \end{aligned} a2−a1b2−b1=width=height=−d1=−d2
这也就是为什么，在第一种情况时，我们可以指定UI的宽和高，因为这两个量在不同分辨率下是保持不变的。
总结
四个锚点分开的时候是最一般的情况，此时面板上的Top，Bottom，Right，Left是不变量。实际上，即使有锚点重合，面板上也可以写这四种属性，因为依然是不变量。
此时，你会问，在第一种情况下，分辨率改变的时候，UI的边框与对应的父边框的距离不是会发生改变么，那为什么还是不变量呢？实际上，比如Top，根本不是表示UI上边框与对应父边框的距离，而是Rect的右上角与对应锚点的纵向距离之差。只是，Unity提供的几种锚点都挂在了父边框上，所以我们那样理解也是没有错的，但是不能推到一般情况。
实际上，我觉得UGUI提供的几种就完全足够用了。我们在玩一款游戏的时候，看到一个UI，查看它在不同分辨率下的表现，宽度和位置是否发生改变，发生怎样的改变，就可以大致推断出它所使用的锚点类型甚至UI pivot比例坐标的设置。
讨论
UGUI是一种绝对距离绑定和相对比例绑定相结合的设计哲学。
我们可以先思考，如果我们设计一个UI系统，如何解决其在不同分辨率下的表现问题。最简单的就是将UI的四个角与父物体的四个角的绝对距离绑定，假设此时父物体是最上层的Canvas，因为这个Canvas会自动充斥整个屏幕空间，所分辨率改变的时候，当前物体也会自动拉伸。
这种简单的绝对距离绑定可以实现小屏幕下，UI变小，大屏幕下，UI变大的效果，满足一定程度的自适应。可惜的是，这样绑定会破坏UI原本的比例，包括UI中心在屏幕中的位置的比例和UI宽高占屏幕大小的比例。这种比例一旦被破坏，容易形成UI相互交叉，穿插的情况。
所以我们可以换成比例变化，按照原本的比例确定物体的位置和宽高。然而这还会带来问题，最大的问题是，在屏幕的分辨率的比例和UI的宽高比例不相等的时候，我们会破坏物体的宽高比例。比如原本物体宽高之比是4：3，但是我们强行按照原本宽高在屏幕中的占比分别拉伸宽高，拉伸之后，宽高之比就不一定是4：3了。UI的宽高比例被破坏，里面的内容显示就会看起来很奇怪。
UGUI结合了上述两种解决方案，它在UI的外层套了一个虚拟框，虚拟框按照比例变化来做自适应，同时UI相对虚拟框按照绝对距离绑定来做自适应，虚拟框的四个角就是所谓的锚点。