手眼标定详述(坐标系介绍，二维、三维的手眼标定方法@九点法、AX=XB)

1. 写在前面

手眼标定实际上就是为了让机械臂知道相机拍出来的物品相对于机械臂在什么位置，所以无论下面的哪一种实际都是建立相机坐标系与机械臂坐标系的映射关系。

• 另外，相机标定的内容可以参考这里https://blog.csdn.net/m0_52785249/article/details/125973858

2. 手眼标定基本分类

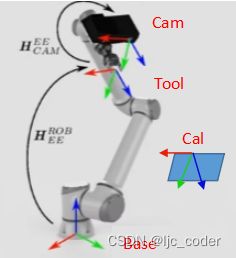
2.1 手眼标定坐标系

Base坐标系(基坐标系)	描述机械臂基座的位置
Tool坐标系(工具坐标系)	描述机械爪(机械臂末端)的位置
Cam坐标系(相机坐标系)	描述相机的位置
Cal坐标系(标定板坐标系)	描述标定板的位置

2.2 眼在手外（EYE TO HEAD）

• 如下图所示，眼在手外是将相机固定在相机平面；标定板固定在机械臂末端，通过移动机械臂来获取标定图像。
  

• 由于眼在手外标定时，Base坐标系和Cam坐标系的位置是固定的，因此眼在手外主要是求这两个坐标系的关系。

2.3 眼在手上（EYE IN HEAD）

• 如下图所示，眼在手上是将相机固定在机械臂末端；标定板固定在物品平面，通过移动机械臂来获取标定图像。
  

• 同理，眼在手上时，相机坐标系和工具坐标系的位置是相对不变的。因此，标定的就是相机坐标系和工具坐标系的关系。

3. 九点法（二维）- 算法实现流程

• 对于二维的手眼标定，广泛采用的方法是九点法：
  1. 在获得相机参数后，指定九个点，先通过相机获得在相机坐标系下这九个点的坐标（2d）。
  2. 再通过示教器将机械臂分别移到九个点的位置，并获取对应在机械臂末端坐标系下的九个点坐标（2d）。
  3. 最后，建立两者的映射关系，即可以表达相机坐标系到机械臂坐标系的关系。

4. AX=XB方法（二维或三维）- 推导 < 什么是AX=XB >

4.1 坐标系转换&运算规则

对于旋转矩阵，坐标系转化（A>>C）表示为：
$${}_C^A{R}^{}{=}_B^A{R}^{}{\ast }_C^B{R}^{}$$

对于平移阵，坐标系转化（A>>C）表示为：
$${}_C^A{T}^{}{=}_B^A{T}^{}{+}_B^A{R}^{}{}_C^B{T}^{}$$

由此，我们可以看到，平移阵的转化关系是比较复杂的，因此，我们引入了齐次坐标系。

4.1.1 齐次坐标系

三维坐标系下的点>>齐次坐标	$$a=(x,y,z{)}^T>>a^{{}^{\prime }}=(x,y,z,1{)}^T$$
齐次坐标系下的点>>三维坐标	$$p=(a,b,c,d{)}^T>>p^{{}^{\prime }}=(\frac{a}{d},\frac{b}{d},\frac{c}{d}{)}^T$$

4.2 实际坐标系转换公式推导

• 复习一下各个坐标系的简称：

Base	基坐标系
Tool	工具坐标系（机械臂末端坐标系）
Cam	相机坐标系
Cal	标定板坐标系

---

（例）基坐标系到工具坐标系的齐次变换阵组成表示为：

$${}_{Base}^{Tool}{R}^{}$$	旋转阵R
$${}_{Base}^{Tool}{T}^{}$$	平移阵T
$${}_{Base}^{Tool}{M}^{}=\left[\begin{array}{cc}{}_{Base}^{Tool}{R}^{}& {}_{Base}^{Tool}{T}^{}\\ 0& 1\end{array}\right]$$	齐次变换阵M

4.2.1 眼在手外

• 眼在手外的标定，我们希望得到基坐标系到相机坐标系的变换 (对于opencv的handeyecalibrate函数，将其输入的机械臂姿态改为base->tool,则得到的输出是相机到基坐标系，与本文这里的示例相反，需要注意!!!) ，表示为 ：
  $${}_{Base}^{Cam}{M}^{}{=}_{Cal}^{Cam}{M}^{}{\ast }_{Tool}^{Cal}{M}^{}{\ast }_{Base}^{Tool}{M}^{}$$

---

其中:

$${}_{Cal}^{Cam}{M}^{}$$	可以通过拍摄标定板图片直接获得(基于相机标定获得的内参和畸变系数)
$${}_{Base}^{Tool}{M}^{}$$	可以通过机械臂末端位姿参数获得(通过示教器可直接获得机械臂位姿来表示机械臂的坐标系)
$${}_{Tool}^{Cal}{M}^{}$$	由于标定板固定在机械臂末端，所以对每组图片，该变换阵都一样(可以在联立方程组时直接消掉)

我们先将Tool>>Cal的变换阵写成：
$${}_{Tool}^{Cal}{M}^{}{=}_{Cal}^{Cam}{M}^{-1}{\ast }_{Base}^{Cam}{M}^{}{\ast }_{Base}^{Tool}{M}^{-1}$$

对于拍摄的多张图像，我们用M₁、M₂…M_n来表示不同图像的变换阵，联立两次变换方程，（消掉Tool>>Cal的变换阵）得到下式：
$${}_{Cal}^{Cam}{M}_1^{-1}{\ast }_{Base}^{Cam}{M}^{}{\ast }_{Base}^{Tool}{M}_1^{-1}{=}_{Cal}^{Cam}{M}_2^{-1}{\ast }_{Base}^{Cam}{M}^{}{\ast }_{Base}^{Tool}{M}_2^{-1}$$

---

我们通过下表将整个变换总结为AX=XB的形式：

$${}_{Cal}^{Cam}{M}_2^{}{\ast }_{Cal}^{Cam}{M}_1^{-1}{\ast }_{Base}^{Cam}{M}^{}{=}_{Base}^{Cam}{M}^{}{\ast }_{Base}^{Tool}{M}_2^{-1}{\ast }_{Base}^{Tool}{M}_1^{}$$ …
$${}_{Cal}^{Cam}{M}_n^{}{\ast }_{Cal}^{Cam}{M}_{n-1}^{-1}{\ast }_{Base}^{Cam}{M}^{}{=}_{Base}^{Cam}{M}^{}{\ast }_{Base}^{Tool}{M}_n^{-1}{\ast }_{Base}^{Tool}{M}_{n-1}^{}$$
即：

$${}_{Base}^{Cam}{M}^{}$$	X
$${}_{Cal}^{Cam}{M}_2^{}{\ast }_{Cal}^{Cam}{M}_1^{-1}$$…$${}_{Cal}^{Cam}{M}_n^{}{\ast }_{Cal}^{Cam}{M}_{n-1}^{-1}$$	A
$${}_{Base}^{Tool}{M}_2^{-1}{\ast }_{Base}^{Tool}{M}_1^{}$$ …$${}_{Base}^{Tool}{M}_n^{-1}{\ast }_{Base}^{Tool}{M}_{n-1}^{}$$	B

4.2.2 眼在手上

• 眼在手上，期望的转化阵为工具坐标系（机械臂末端坐标系）到相机坐标系，表示为：
  $${}_{Tool}^{Cam}{M}^{}{=}_{Cal}^{Cam}{M}^{}{\ast }_{Base}^{Cal}{M}^{}{\ast }_{Tool}^{Base}{M}^{}$$

---

其中:

$${}_{Cal}^{Cam}{M}^{}$$	可以通过拍摄标定板图片直接获得(基于相机标定获得的内参和畸变系数)
$${}_{Tool}^{Base}{M}^{}$$	可以通过机械臂末端位姿参数获得(通过示教器可直接获得机械臂位姿来表示机械臂的坐标系)
$${}_{Base}^{Cal}{M}^{}$$	由于标定板固定在一个位置不动，所以对每组图片，该变换阵都一样(可以在联立方程组时直接消掉)

我们先将Cal>>Base的变换阵写成：
$${}_{Base}^{Cal}{M}^{}{=}_{Cal}^{Cam}{M}^{-1}{\ast }_{Tool}^{Cam}{M}^{}{\ast }_{Tool}^{Base}{M}^{-1}$$
基于眼在手外的原理，将眼在手上的变换阵求解表示为：

$${}_{Tool}^{Cam}{M}^{}$$	X
$${}_{Cal}^{Cam}{M}_2^{}{\ast }_{Cal}^{Cam}{M}_1^{-1}$$…$${}_{Cal}^{Cam}{M}_n^{}{\ast }_{Cal}^{Cam}{M}_{n-1}^{-1}$$	A
$${}_{Tool}^{Base}{M}_2^{-1}{\ast }_{Tool}^{Base}{M}_1^{}$$ …$${}_{Tool}^{Base}{M}_n^{-1}{\ast }_{Tool}^{Base}{M}_{n-1}^{}$$	B

4.3 求解

首先将A,B,X表示为齐次阵的形式：

$$\left[\begin{array}{cc}{R}_X^{}& T_X^{}\\ 0& 1\end{array}\right]$$	X
$$\left[\begin{array}{cc}{R}_A^{}& T_A^{}\\ 0& 1\end{array}\right]$$	A
$$\left[\begin{array}{cc}{R}_B^{}& T_B^{}\\ 0& 1\end{array}\right]$$	B

---

即可将 AX=XB 拆解为：
$$R_A{R}_X=R_X{R}_B$$
$$(R_A-I)T_X=R_X{T}_B-T_A$$

---

关于上式具体的求解：

• 可以基于优化方法的思想(高斯牛顿的方法)，移到一边后求取误差项，然后通过非线性最优化的方法，将误差最小化，直接拟合出 R 和 T。
• （常用） 也可以基于两步法的思想，先求R再求T，具体可以参考Navy_HandEye或Tsai_HandEye等方法。

5. AX=XB方法（二维或三维）- 算法实现流程（总结）

下面以EYE IN HAND为例，描述实际的算法实现流程：

1. 相机标定获得像素坐标系到世界坐标系（标定板坐标系）的变换关系。
   • 由于该相机标定结果会用于手眼标定，因此相机标定时，标定板固定位置不动，手眼组合体变换姿态拍摄图片。
2. A 通过在不同姿态下读取相机外参（相机相对于世界坐标系，即标定板坐标系的位姿）获得的位姿矩阵求得。
3. B 通过示教器读取不同位姿下的机械臂末端相对于基座的坐标求得。
4. 求解变换阵 X
   这里可以参考：https://blog.csdn.net/wanggao_1990/article/details/81435660

源码相关的博文

• https://blog.csdn.net/wanggao_1990/article/details/81435660
• https://blog.csdn.net/panpan_jiang1/article/details/80429937
• https://blog.csdn.net/panpan_jiang1/article/details/80402967