基于FPGA的小数计算学习
1.前言
在展开学习之前,我先回答网友的一些提问,问题如下所示:
No.1:ARM、DSP、FPGA到底学习哪个好?
这个问题也是我上大学期间遇到过的问题,当年我的做法像小学的一篇文章《小猫钓鱼》中的小花猫一样,一会儿扑蝴蝶,一会儿抓鱼,总是三心二意,最后没有任何收获。
我想现在有很多大学生或者研究生还是有同样的问题,不知道到底学习哪个方向,在浑浑噩噩中度过了大学或者研究生时光,毕业时就变成了失业....
首先,我们把这三个嵌入式在工程中的应用方向介绍一下:ARM一般做控制用的比较多,DSP适合做算法运算、FPGA适合做大数据流的处理;所以说没有学哪个好,我们应该选择适合自己的就可以了。
然后,我们讲一下现在企业是如何做项目的。一般情况,像做通信方向都会采用DSP+FPGA的设计来做;像控制方向都会采用ARM+FPGA的设计来做,FPGA的应用方向就比较多了,例如,控制、通信、医疗、安防、图像等。
最后,我们来说一下将来的发展趋势。我个人觉得目前的电子行业绕不开的两个因素(无论哪个专业方向都一样):一个是数据量越来越多,另一个是处理速度要求越来越快。谁能够从容的应对这两个问题,那么就会生存下去。我个人觉得处理速度是更重要的,就像电影《功夫》里终级杀人王说的一样:“天下武功,唯快不破!”
说了半天到底选择哪个嵌入式呢?我觉的就两点:第一点,就是选择一个方向学习,不要三心二意;第二点,选择适合你以及适合将来发展的就行了。
如果让我重新选择的话,我仍然会选择FPGA,因为我对它爱的深沉,哈哈!(绝对不能让我老婆知道,不然就让我跪搓衣板了。)
No.2 FPGA可以进行小数运算吗?
FPGA完全可以进行小数运算。在平时工作,我遇到过一些路人说FPGA搞不了小数运算(也称作浮点数运算),我只能说他们是外行人,不懂胡说;我只当乱风过耳,不予理睬。
当年我上学期间,由于自己学艺不精,当时也觉得FPGA不能做浮点数运算,不能像C语言那样,但是工作后通过做项目以及和大神们交流,发现原来FPGA也是可以做浮点数运算的。当年和和一位大神聊天,问他同样的问题;他的回答
一下点醒了我!(原话核心意思是无论什么类型的数据在计算机里永远都是“0”或“1”) 听完后我脑子里就想到了一句古话:“听君一席话,胜读十年书啊!
这篇文章就专门对FPGA的小数运算(浮点数运算)进行介绍,希望能对大家有所帮助!
2.浮点数运算方法介绍
2.1用标准浮点数形式计算小数
浮点数说的通俗点就是我们说的小数,如果按照官方定义一堆名词(我这里不介绍,可以上网查阅),例如C语言中的float类型等。浮点数有单精度和双精度之分,它们的格式如下所示:
- 1. 单精度和双精度的浮点数说明
| 名称 |
符号位 |
价码 |
尾数 |
| 单精度浮点数 |
31bit:1代表负数;0代表正数 |
[30:23] |
[22:0] |
| 双精度浮点数 |
63bit:1代表负数;0代表正数 |
[62:52] |
[51:0] |
这种格式的通俗理解就是小学数学学习的指数表达式,例如1500可以表示为1.5*10^3,下面我们以单精度浮点数为例,做个说明吧。
单精度浮点数共32bit,最高位代表的是符号位,30-23bit代表的是价码值(通俗就是指数值)默认的空值为十进制127;尾数就是有效数值了。例如,现在有个数据为1500,变成指数形式为1.5*10^3,如何用单精度表示呢?该数据是正数,所以符号位填写“0”,指数次幂为3,价码值=127+3=130(如果是负指数就执行减法);有效数据为1.5可以分为整数部分和小数部分,整数部分是按照2^N来计算,1=2^0;小数部分按照2^(-N)来计算,0.5=2^(-1);所以整个表达数为1100_0000_0000_0000_0000_000
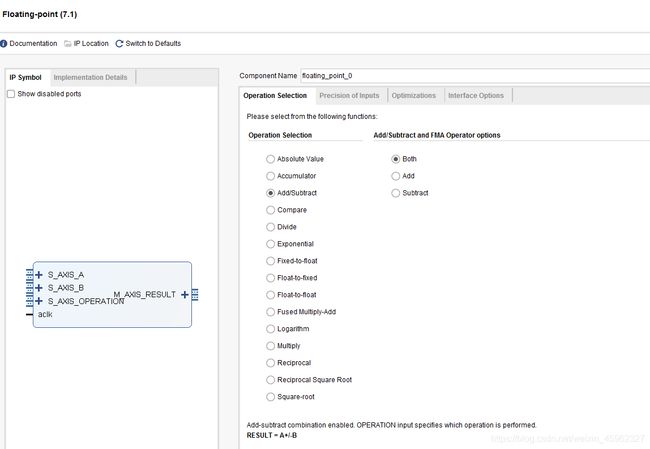
2.2用FPGA自带的IP核计算小数
Xilinx或者Altera公司都带有浮点数运算的IP核,直接调用IP进行计算相对方便,使用者不用关心浮点数的转化格式。例如,XIlinx的IP如下图所示。
2.3放大法计算小数
这种方式在实际工程中最常用的,就是先把参与运算的小数放大N倍后,让它变成整数参与运算,最后,将运算结果除以放大倍数就可以了。
例如,25*2.123运算,如下步骤所示:
第一步:2.123*1000变为2123;
第二步:25*2123;
第三步:结果除以1000,获取整数部分即可。
2.4定点数计算小数
定点数其实和单精度浮点数相似,但是去除了那种复杂的格式,如下图所示。
| 符号位 | 整数部分 | 小数部分 |
在实际操作中,一般需要数据交互双方沟通,主要沟通负数是不是要遵循通用的负数形式(一般是取反加1);在实际项目中,为了简便操作一般就是改符号位,有效数据直接用正数据的值代表。
注意:如果不用标准模式,一定要双方沟通好,不然就容易出现问题!!!!
总结:这几种方式都可以在实践中应用,大家可以根据实际情况选择方法。当然,我个人只了解这几种方式,可能还有其他方式,大家可以上网查下资料。
3.浮点数运算程序设计
前面已经对浮点数进行了介绍,本章节开始展开程序设计。我们分为两部分设计:
- 实现小数部分数据转换成二进制的程序设计
- 实现定点数的小数运算程序设计
3.1小数部分十进制数据转成二进数据程序设计
在数字世界里,任何的数字表示都用0或者1表示的,所以我们要把小数部分的十进制数据先转化为二进制。在二进制世界里,数据的表示是用2的指数进行表示,整数部分的数据表示是按照2的正指数表示,小数部分是按照2的负指数表示的。
例如,一个数据为3.75,该数据包含整数部分和小数部分。
整数部分用二进制表示为 :11
小数部分用二进制表示为 :11
这里我重点把小数部分转二进制详细说一下:
第一步:0.75可以看作是0.5+0.25组成;
第二步:0.5相当于是1/(2^1),0.25相当于是1/(2^2)
第三步:根据第二步将对应的位置上填写1或0;1/(2^1)是表示有效数据的所以填写为1,同理1/(2^2)表示有有效数据填写为1
我们要遵循这个整数部分的数据表示是按照2的正指数表示,小数部分是按照2的负指数表示的的原则来设计程序。在程序设计中转化的小数二进制位数设计为可变模式(使用者可以设计转化的二进制位数)
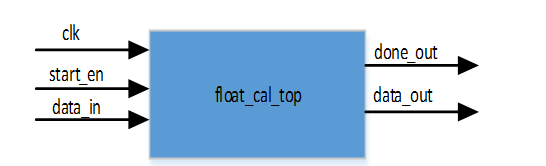
| 名称 |
方向 |
位宽 |
说明 |
| clk |
Input |
1 |
工作时钟 |
| start_en |
Input |
1 |
计算信号 |
| data_in |
Input |
32 |
输入数据 |
| dout_out |
Output |
size |
结果数据,该数据位宽根据需求可以转换对应的位数 |
| done_out |
Output |
1 |
计算完成信号 |
module flaot_cal_top#(
parameter SIZE=24,//输出的二进制位数设置
parameter FLOAT_mulit=1000//转换倍数设置
)
(
input [31:0] data_in ,//输入的小数部分的整数表示
input start_en ,//启动信号
input clk ,//时钟信号
output [SIZE-1:0] data_out ,//计算的结果
output done_out //计算完成标志信号
);
wire [31:0] data_reg[SIZE:0] ;//数组表达格式
wire done[SIZE:0] ;//数组表达格式
wire [SIZE:0] data_out_reg ;
assign done_out = done[SIZE];
assign data_out = data_out_reg[SIZE-1:0];
//------------------------------采用generate语法编写代码------------------
genvar i;
generate
for(i=0;i测试文件:
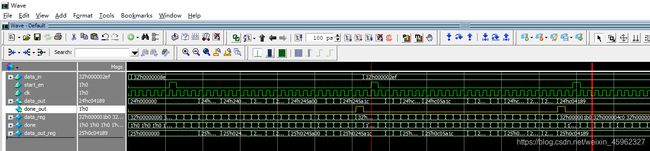
测试两个小数部分数据:0.142和0.751
如上图黄色的高电平信号处为算出的0.142和0.751的二进制数据,它们分别为24位的二进制表示;该程序计算结果和理论值相同。
可以关注微信公众号《FPGA的故事》!