剑指Offer-推理二叉树

剑指Offer-推理二叉树

LCR 124. 推理二叉树

题目如下

某二叉树的先序遍历结果记录于整数数组 preorder，它的中序遍历结果记录于整数数组 inorder。请根据 preorder 和 inorder 的提示构造出这棵二叉树并返回其根节点。

注意：preorder 和 inorder 中均不含重复数字。

示例 1：

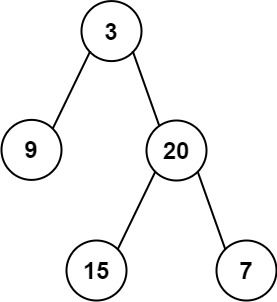
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]

输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

思路

首先我们要知道，前序和中序各代表着什么。

前序即是：根左右

中序则是：左根右

因此我们可以通过前序数组得到根节点，而在中序数组中，得到根节点的左右子节点。

具体如下：

preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

preorder里头的第一个元素必定是根节点，这里为3，在inorder里头，3的左右子节点则是

[9]和[15,20,7]

而每一个根节点都可以像这样子构建，因此这道题是体现了分治的思想。

递归函数

我们需要返回的是一个结点，因此返回值为：TreeNode*

在寻找左右子节点时，我们需要界定其范围，因此参数加入left和right表示左右子树的范围。

函数如下：

TreeNode* fun(int left,int right){
	
}

递归终止条件

当left > right 时则说明已不存在节点了（left==right则只有一个节点）

单次递归逻辑

如我们上面说的那样

1. 首先获取根节点的值
2. 创建根节点
3. 获取根节点在中序数组中的位置
4. 构建左右子树

代码如下

class Solution {
private:
    int cur_pos;
    unordered_map<int,int> hamp;
    TreeNode* fun(int left,int right,vector<int> preorder, vector<int> inorder){
        if(left>right) return nullptr;
        // 获取根节点值
        int root_val = preorder[cur_pos++];
        // 构建根节点 
        TreeNode* root = new TreeNode(root_val);
        // 获取根节点在inorder中的位置
        int index = hamp[root_val];
        // 构建左右子树
        root->left = fun(left,index-1,preorder,inorder);
        root->right = fun(index+1,right,preorder,inorder);
        return root;
    }
public:
    TreeNode* deduceTree(vector<int>& preorder, vector<int>& inorder) {
        cur_pos = 0;
        for(int i=0;i<inorder.size();i++){
            hamp[inorder[i]] = i;
        }
        return fun(0,inorder.size()-1,preorder,inorder);
    }   
};

优化版本

注意到上面代码中有一个cur_pos，每次–，用来轮询根节点的值，实际上并不需要一个一个都去访问。

在构建左右子树是，我们可以直接锁定住根节点的位置。

原理是：中序里面左右子树的长度是等于前序数组里头左右子树的长度的

因此我们可以通过计算得到左右子树根节点在前序数组里面的位置。

我们在每次递归时都加入一个新参数：root_index

对于左子树来说，根节点就是当前的根节点++（往右推一位）

对于右子树来说，根节点就是当前的根节点+左子树的长度+1

代码如下

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    unordered_map<int,int> hamp;
    TreeNode* fun(int root_index,int left,int right,vector<int> preorder, vector<int> inorder){
        if(left>right) return nullptr;
        // 获取根节点值
        int root_val = preorder[root_index];
        // 构建根节点 
        TreeNode* root = new TreeNode(root_val);
        // 获取根节点在inorder中的位置
        int index = hamp[root_val];
        // 构建左右子树
        root->left = fun(root_index+1,left,index-1,preorder,inorder);
        root->right = fun(root_index+index+1-left,index+1,right,preorder,inorder);
        return root;
    }
public:
    TreeNode* deduceTree(vector<int>& preorder, vector<int>& inorder) {
    
        for(int i=0;i<inorder.size();i++){
            hamp[inorder[i]] = i;
        }
        return fun(0,0,inorder.size()-1,preorder,inorder);
    }   
};
        for(int i=0;i<inorder.size();i++){
            hamp[inorder[i]] = i;
        }
        return fun(0,0,inorder.size()-1,preorder,inorder);
    }   
};