强化学习之马尔科夫过程

马尔可夫过程

马尔可夫决策过程（Markov Decision Processes,MDPs）是对强化学习问题的数学描述。几乎所有的RL问题都能用MDPs来表述：

• 最优控制问题可以描述为连续MDPs
• 部分观测环境可以转化成POMDPs
• 赌博机问题是只有一个状态的MDPs

本文中介绍的MDPs是在全观测的环境下进行的！

马尔科夫性

如果在t时刻的状态 St S t 满足如下等式，那么这个状态被称为马尔科夫状态，或者说该状态满足马尔科夫性。

P[St+1|St]=P[St+1|S1,...,St] P [ S t + 1 | S t ] = P [ S t + 1 | S 1 , . . . , S t ]

• 状态 St S t 包含了所有历史相关信息，或者说历史的所有状态的相关信息都在当前状态 St S t 上体现出来
• 一旦 St S t 知道了，那么 S1,S2,...,St−1 S 1 , S 2 , . . . , S t − 1 都可以被抛弃
• 数学上可以认为状态是将来的充分统计量，这里要求环境全观测，比如下棋时，只关心当前局面，打俄罗斯方块时，只关心当前屏幕

状态转移矩阵

状态转移概率指从一个马尔科夫状态s跳转到后继状态 s′ s ′ 的概率

Pss′=P[St+1=s′|St=s] P s s ′ = P [ S t + 1 = s ′ | S t = s ]

所有的状态组成行，所有的后继状态组成列，我们得到状态转移矩阵

P=⎡⎣⎢⎢p11⋮pm1⋯⋱⋯p1n⋮pmn⎤⎦⎥⎥ P = [ p 11 ⋯ p 1 n ⋮ ⋱ ⋮ p m 1 ⋯ p m n ]

n表示状态的个数，每行元素相加和等于1

状态转移函数

我们可以将状态转移概率写成函数形式

P(s′|s)=P[St+1=s′|St=s] P ( s ′ | s ) = P [ S t + 1 = s ′ | S t = s ]

• ∑s′P(s′|s)=1 ∑ s ′ P ( s ′ | s ) = 1
• 状态数量太多或者无穷大（连续状态）时，更适合使用状态转移函数，此时 ∫s′P(s′|s)=1 ∫ s ′ P ( s ′ | s ) = 1

马尔可夫过程（Markov process,MP）

马尔可夫过程是一个无记忆的随机过程，即一些马尔可夫状态的序列，马尔可夫过程可以由一个二元组来定义 < S,P >，S表示状态的集合，P描述状态转移矩阵
注：虽然我们不知道P的具体值，但是通常我们假设P存在且稳定，当P不稳定时，不稳定环境在线学习，快速学习

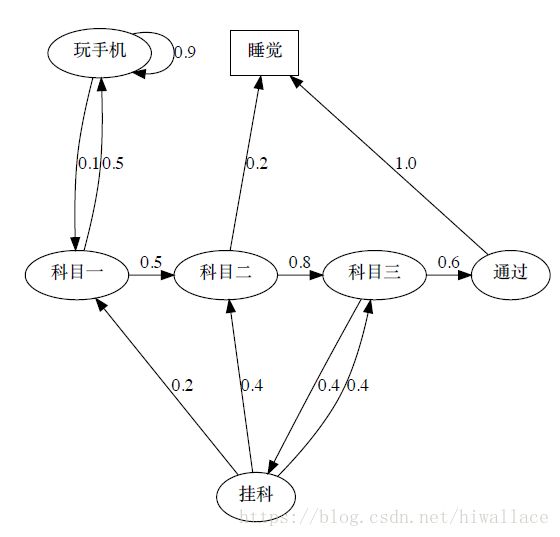
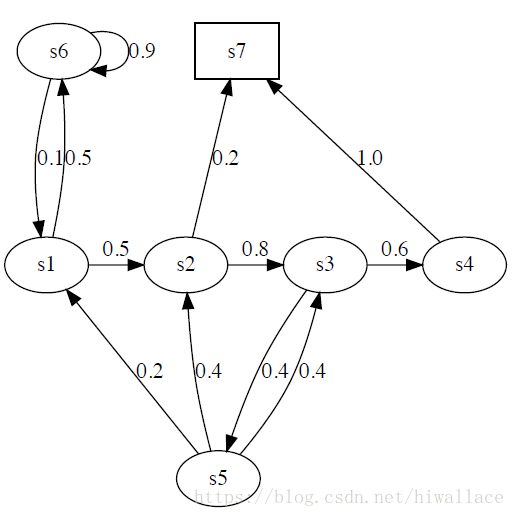
如上图：

• 一个学生每天需要学习三个科目，然后通过测验
• 有的可能智学苑两个科目之后直接睡觉
• 一旦挂科有可能需要重新学习某些科目
• 该过程用椭圆表示普通状态，每条线上的数字表示从一个状态跳转到另一个状态的概率
• 方块表示终止状态
• 终止状态的定义有两种：
  
  • 时间终止
  • 状态终止

由于马尔可夫过程可以用图中的方块和线条表示，所以马尔可夫过程也成为马尔可夫链

片段

强化学习中，从初始状态 S1 S 1 到终止状态的序列过程，被称为一个片段 S1,S2,...,ST S 1 , S 2 , . . . , S T

• 如果一个任务总以终止状态结束，那么这个任务被称为片段任务
• 如果一个任务会没有终止状态，会被无限执行下去，被称为连续性任务

状态转移矩阵：

马尔可夫奖励过程（MRP）

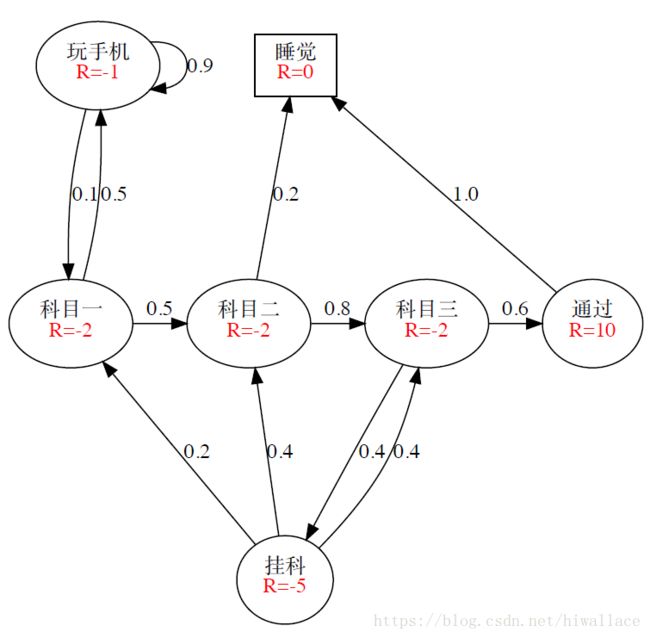
马尔可夫链主要描述的是状态之间的转移关系，在这个转移关系上赋予不同的奖励值即得到了马尔可夫奖励过程。

• S代表状态的集合
• P表示状态转移矩阵
• R表示奖励函数，R(s)描述在状态s的奖励 R(s)=E[Rt+1|St=s] R ( s ) = E [ R t + 1 | S t = s ]
• γ γ 表示衰减因子， γ∈[0,1] γ ∈ [ 0 , 1 ]

回报值

奖励值是对每一个状态的评价，回报值是对每一个片段的评价
回报值（return Gt G t ）是从时间t处开始的累计衰减奖励

• 对于片段性任务
  

  Gt=Rt+1+γRt+2+...+γT−t−1RT=∑k=0T−t−1γkRt+k+1 G t = R t + 1 + γ R t + 2 + . . . + γ T − t − 1 R T = ∑ k = 0 T − t − 1 γ k R t + k + 1

• 对于连续性任务
  

  Gt=Rt+1+γRt+2+...=∑k=0∞γkRt+k+1 G t = R t + 1 + γ R t + 2 + . . . = ∑ k = 0 ∞ γ k R t + k + 1

终止状态等价于自身转化概率为1，奖励为0的状态

因此我们能够将片段性任务和连续性任务统一表达

Gt=∑k=0T−t−1γkRt+k+1 G t = ∑ k = 0 T − t − 1 γ k R t + k + 1

当T= ∞ ∞ 时，表示连续性任务，否则为片段性任务

关于衰减系数 γ γ

• 影响未来的因素不仅包含当前，所以需要用多状态的统计量。而我们对未来的把握是逐步衰减的，一般情况下更关注短时间的反馈
• 指数衰减是对回报值的有界保证，避免了循环MRP和连续性MRP情况下回报值编程无穷大

值函数

一个MRP的值函数定义为：

v(s)=E[Gt|St=s] v ( s ) = E [ G t | S t = s ]

这里的值函数针对的是状态s，故称为状态值函数，也称为V函数， Gt G t 是一个随机变量
从相同的初始状态，不同的片段有不同的回报值，值函数就是它们的期望值。

状态值函数是与策略 π π 相对应的，因为策略 π π 决定了累计回报G的状态分布

MRPs中的贝尔曼方程

值函数的表达式可以分解成两部分：瞬时奖励 Rt+1 R t + 1 ，后继状态 St+1 S t + 1 的值函数乘上一个衰减系数

v(s)=E[Gt|St=s]　　　　　　　　　　　=E[Rt+1+γRt+2+γ2Rt+3+...|St=s]　　　　　　　　　　　=E[Rt+1+γ(Rt+2+γRt+3+...)|St=s]　　　　　=E[Rt+1+γGt+1|St=s]　　　　　　=E[Rt+1+γv(St+1)|St=s] v ( s ) = E [ G t | S t = s ] 　 　 　 　 　 　 　 　 　 　 　 = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . | S t = s ] 　 　 　 　 　 　 　 　 　 　 　 = E [ R t + 1 + γ ( R t + 2 + γ R t + 3 + . . . ) | S t = s ] 　 　 　 　 　 = E [ R t + 1 + γ G t + 1 | S t = s ] 　 　 　 　 　 　 = E [ R t + 1 + γ v ( S t + 1 ) | S t = s ]

如果已知转移矩阵P，则

v(s)=E[Rt+1+γv(St+1)|St=s]　　　　　=E[Rt+1|St=s]+γE[v(St+1)|St=s]=R(s)+γ∑s′∈SPss′v(s′) v ( s ) = E [ R t + 1 + γ v ( S t + 1 ) | S t = s ] 　 　 　 　 　 = E [ R t + 1 | S t = s ] + γ E [ v ( S t + 1 ) | S t = s ] = R ( s ) + γ ∑ s ′ ∈ S P s s ′ v ( s ′ )

使用矩阵-向量的形式表达贝尔曼方程，即

v=R+γPv v = R + γ P v

假设状态集合 S=s1,s2,...,sn S = s 1 , s 2 , . . . , s n ,则

⎡⎣⎢⎢v(s1)⋮v(sn)⎤⎦⎥⎥=⎡⎣⎢⎢R(s1)⋮R(sn)⎤⎦⎥⎥+γ⎡⎣⎢⎢⎢Ps1s1⋮P(sns1)⋯⋱⋯Ps1sn⋮Psnsn⎤⎦⎥⎥⎥⎡⎣⎢⎢v(s1)⋮v(sn)⎤⎦⎥⎥ [ v ( s 1 ) ⋮ v ( s n ) ] = [ R ( s 1 ) ⋮ R ( s n ) ] + γ [ P s 1 s 1 ⋯ P s 1 s n ⋮ ⋱ ⋮ P ( s n s 1 ) ⋯ P s n s n ] [ v ( s 1 ) ⋮ v ( s n ) ]

贝尔曼方程本质上是一个线性方程，可以直接解：

v=R+γPv(1−γP)v=Rv=(1−γP)−1R v = R + γ P v ( 1 − γ P ) v = R v = ( 1 − γ P ) − 1 R

计算复杂度为 O(n3) O ( n 3 ) ，要求已知状态转移矩阵P， 直接求解的方式仅限于的MRPs

马尔可夫决策过程

马尔可夫过程（MP）和马尔可夫奖励过程是去观察其中的状态转移现象，去计算回报值，对于一个RL问题，我们更希望去改变状态转移的过程，最大化回报值。通过在MRP中引入决策即得到了马尔可夫决策过程（Markov Decision Processes,MDPs）
定义：
一个马尔科夫决策过程由一个五元组组成 γ γ >

• S表示状态的集合
• A表示动作的集合
• P描述状态转移矩阵， Pass′=P[St+1=s′|St=s,At=a] P s s ′ a = P [ S t + 1 = s ′ | S t = s , A t = a ]
• R表示奖励函数，R(s,a)描述在状态s做动作a的奖励， R(s,a)=E[Rt+1|St=s,At=a] R ( s , a ) = E [ R t + 1 | S t = s , A t = a ]
• γ γ 表示衰减因子， γ∈[0,1] γ ∈ [ 0 , 1 ]

上图为MDPs的链图，对比MRP的马尔可夫链图，不同点在于：
- 针对状态的奖励变成了的奖励
- 通过动作进行控制的状态转移由原来的状态转移概率替换为动作
- MDP只关注哪些可以做决策的动作，被动的状态转移关系被压缩成一个状态（被动状态指无论做任何动作，状态都会发生跳转）

策略

MDPs中的策略是智能体能够控制的策略，不受控制的都认为是环境的一部分。一个策略（Policy） π π 是在给定状态下的动作的概率分布

π(a|s)=P[At=a|St=s] π ( a | s ) = P [ A t = a | S t = s ]

• 策略是对智能体行为的全部描述
• MDPs中的策略是基于马尔可夫状态的，而不是基于历史状态的
• 策略是时间稳定的，只与s有关，与时间t无关
• 策略是RL问题的终极目标
• 如果策略的概率分布输出都是独热的（非0即1），那么称为确定策略，否则为随机策略

MDPs与MRPs之间的关系

对于一个MDP问题 γ γ >，如果给定了策略 π π ,则MDP将会退化成MRP， Pπ P π , Rπ R π , γ γ >

Pπss′=∑a∈Aπ(a|s)Pass′Rπs=∑a∈Aπ(a|s)Ras P s s ′ π = ∑ a ∈ A π ( a | s ) P s s ′ a R s π = ∑ a ∈ A π ( a | s ) R s a

MDPs中的值函数

MDPs中的值函数有两种：状态值函数（V函数）和状态动作值函数（Q函数）

状态值函数从状态s开始，使用策略 π π 得到的策略回报值

vπ(s)=E[Gt|St=s] v π ( s ) = E [ G t | S t = s ]

分解成瞬时奖励和后继状态：

vπ(s)=Eπ[Rt+1+γvπ(St+1)|St=s] v π ( s ) = E π [ R t + 1 + γ v π ( S t + 1 ) | S t = s ]

状态动作值函数从状态s开始，执行动作a，然后使用策略 π π 得到的期望回报值

qπ(s,a)=Eπ[Gt|St=s,At=a] q π ( s , a ) = E π [ G t | S t = s , A t = a ]

分解成瞬时奖励和后继状态：

qπ(s,a)=Eπ[Rt+1+γqπ(St+1,At+1)|St=s,At=a] q π ( s , a ) = E π [ R t + 1 + γ q π ( S t + 1 , A t + 1 ) | S t = s , A t = a ]

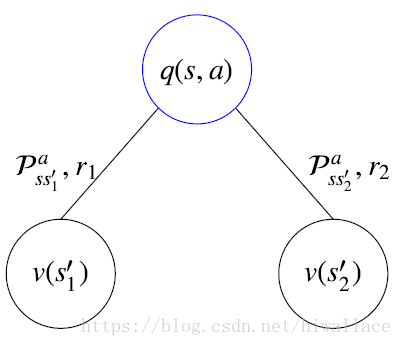
V函数与Q函数之间的相互转化：

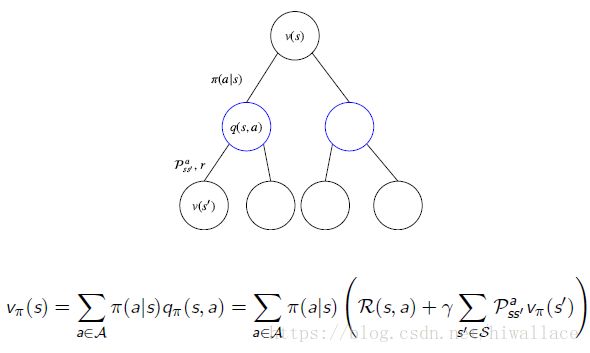
V=>Q： vπ(s)=∑a∈Aπ(a|s)qπ(s,a) v π ( s ) = ∑ a ∈ A π ( a | s ) q π ( s , a )

Q=>V： qπ(s,a)=R(s,a)+γ∑s′∈SPass′Vπ(s′) q π ( s , a ) = R ( s , a ) + γ ∑ s ′ ∈ S P s s ′ a V π ( s ′ )

贝尔曼期望方程V函数

贝尔曼期望方程Q函数

贝尔曼期望方程的矩阵形式

MDPs下的贝尔曼期望方程和MRP的形式相同，

vπ=Rπ+γPπvπ v π = R π + γ P π v π

直接求解可得：

vπ=(1−γPπ)−1Rπ v π = ( 1 − γ P π ) − 1 R π

最优化函数

之前值函数以及贝尔曼期望方程针对的都是给定策略 π π 的情况，是一个评价的问题。现在我们考虑强化学习中的优化问题，即找出最好的策略：
最优值函数指的是在所有策略中的值函数最大值，其中包括最优V函数和最优Q函数：

v∗(s)=maxπvπ(s) v ∗ ( s ) = max π v π ( s )

q∗(s,a)=maxπqπ(s,a) q ∗ ( s , a ) = max π q π ( s , a )

最优值函数指的是一个MDP中所能达到的最佳性能，如果我们找到最优值函数即相当于这个MDP解决了。

最优策略

为了比较不同策略的好坏，我们首先应该定义策略的比较关系：

π≥π′　if　vπ(s)≥vπ′(s),∀s π ≥ π ′ 　 i f 　 v π ( s ) ≥ v π ′ ( s ) , ∀ s

对于任何MDPs问题，总存在一个策略要好于或等于其他所有策略；所有的最优策略都能够实现最优的V函数；所有的最优策略都能够实现最优的Q函数。

最优V函数和最优Q函数存在递归的关系，互转公式如下：
V=>Q:

v∗(s)=vπ∗(s)=∑a∈Aπ∗(a|s)qπ∗(s,a)=maxaqπ∗(s,a)=maxaq∗(s,a) v ∗ ( s ) = v π ∗ ( s ) = ∑ a ∈ A π ∗ ( a | s ) q π ∗ ( s , a ) = max a q π ∗ ( s , a ) = max a q ∗ ( s , a )

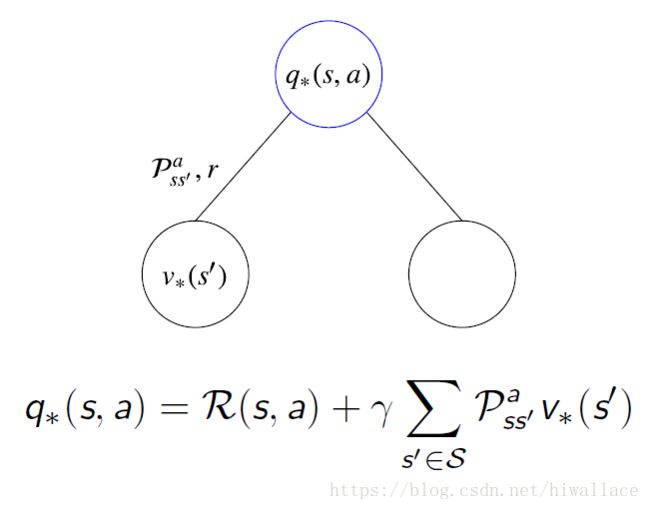
Q=>V:

贝尔曼最优方程：
V函数：

Q函数：

贝尔曼最优方程与贝尔曼期望方程的关系：

• 贝尔曼最优方程本质上利用了 π∗ π ∗ 的特点，将求期望的算子转化成了 maxa m a x a
• 在贝尔曼期望方程中， π π 是已知的，而在最优方程中， π∗ π ∗ 是未知的
• 解贝尔曼期望方程的过程对应了评价，解贝尔曼最优方程的过程对应了优化

MDPs的拓展

• 无穷或连续MDPs

  包含如下情况：

  • 动作空间或状态空间无限可数
  • 动作空间或状态空间无限不可数（连续）
  • 时间连续

• 部分可观测MDPs（POMDPs）

  POMPDs此时观测不等于状态，由七元组构成 γ γ >，其中Z是观测函数

  Zas′o=P[Ot+1=o|St+1=s′,At=a] Z s ′ o a = P [ O t + 1 = o | S t + 1 = s ′ , A t = a ]

  
  观测不满足马尔可夫性，因此不满足贝尔曼方程
  状态未知，属于隐马尔可夫过程
  有时对于POMDPs来说，最优的策略是随机性的

• 无衰减MDPs

  用于各态历经马尔可夫决策过程，各态经历性指平稳随机过程的一种特性
  存在独立于状态的平均奖赏 ρπ ρ π
  求值函数时，需要减去该平均奖赏，否则有可能奖赏爆炸