代码随想录算法训练营第十五天 | 二叉树 part 2 | 层序遍历、反转二叉树、对称二叉树
目录
- 层序遍历
-
- 代码
- 429.N叉树的层序遍历
- 116.填充每个节点的下一个右侧节点指针
- 111.二叉树的最小深度
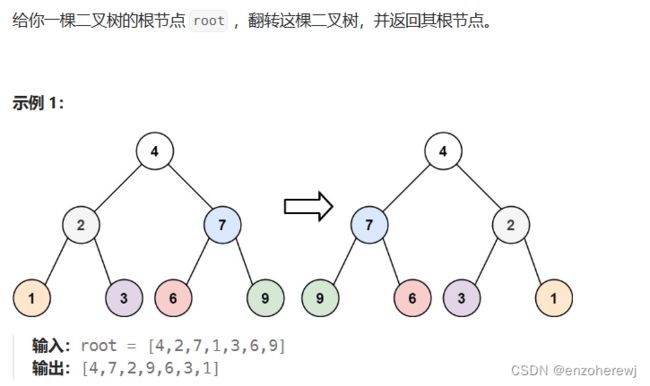
- 226. 翻转二叉树
-
- 思路
- 代码
- 101. 对称二叉树
-
- 思路
- 代码
层序遍历
层序遍历使用队列的结构。
队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
代码
迭代法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
# 这是初始化deque的方式,不能直接写deque(root)
queue = deque([root])
res = []
while queue:
level = []
for i in range(len(queue)):
node = queue.popleft()
level.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
res.append(level)
return res
递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
levels = []
self.helper(root, 0, levels)
return levels
def helper(self, node, level, levels):
if not node:
return
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
self.helper(node.left, level + 1, levels)
self.helper(node.right, level + 1, levels)
今天其他的10题基本上可以用类似的写法写完。有几道题的卡了一会所以记录一下。
429.N叉树的层序遍历
这道题一开始self.children从来没见过是什么结构,后面把self.children打印出来之后发现是a list of nodes.
所以用for child in children,然后append child到queue里面即可。
116.填充每个节点的下一个右侧节点指针
这一题需要用到指针prev来指代前一个node,然后让prev.next等于下一个node。
111.二叉树的最小深度
最小深度就是相当于BFS遍历到的第一个满足node.left is None and node.right is None的node所在的枝的深度。
226. 翻转二叉树
Leetcode
思路
递归法
- 前序遍历:在进入左孩子,右孩子的递归之前,交换左右孩子
- 后序遍历:在进入左孩子,右孩子的递归之后,交换左右孩子
- 中序遍历:如果按照前序,后序遍历的方法递归,会出现问题。使用递归的中序遍历,某些节点的左右孩子会翻转两次。
迭代
具体的细节和前序遍历,后序遍历的时候差不多,只是多加了一句交换的代码。
代码
前序递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return root
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
前序迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return root
stack = [root]
while stack:
node = stack.pop()
node.left, node.right = node.right, node.left
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
return root
101. 对称二叉树
Leetcode
思路
这道题不是简单比较左孩子和右孩子,而是比较左树内侧外侧,和右树内侧外侧。具体如下图:

遍历顺序的区别:
正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。
代码
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
return self.compare(root.left, root.right)
def compare(self, left, right):
#首先排除空节点的情况
if left == None and right != None: return False
elif left != None and right == None: return False
elif left == None and right == None: return True
#排除了空节点,再排除数值不相同的情况
elif left.val != right.val: return False
#此时就是:左右节点都不为空,且数值相同的情况
#此时才做递归,做下一层的判断
outside = self.compare(left.left, right.right) #左子树:左、 右子树:右
inside = self.compare(left.right, right.left) #左子树:右、 右子树:左
isSame = outside and inside #左子树:中、 右子树:中 (逻辑处理)
return isSame
未完待续:还有很多种其他的写法,比如说用队列和栈来实现,等有空了再补上去。