数据结构-双向链表
1.带头双向循环链表:
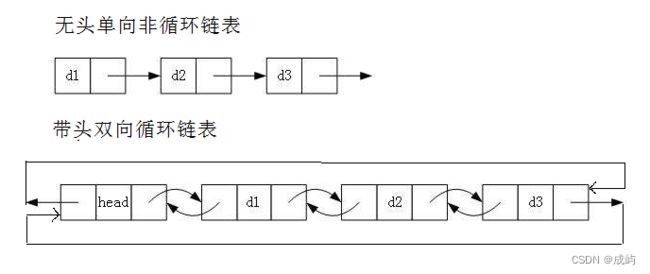
前面我们已经知道了链表的结构有8种,我们主要学习下面两种:
前面我们已经学习了无头单向非循环链表,今天我们来学习带头双向循环链表:
带头双向循环链表:结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构,都是带头双向循环链表。另外这个结构虽然结构复杂,但是使用代码实现以后会发现结构会带来很多优势,实现反而简单了,后面我们代码实现了就知道了
带头双向循环链表不需要二级指针,因为我们刚开始就为其开辟了一个节点,叫做哨兵位头节点,它是结构体中的指针,用结构体指针就能改变它,而要改变结构体外面的指针才会用二级指针。
双向循环链表顾名思义,除了哨兵位头节点以外,每个节点里面应该有两个指针,下面我们定义一个结构体:
typedef int ListDatatype;
typedef struct ListNode
{
struct ListNode* prev;
struct ListNode* next;
ListDatatype data;
}LTNode;prev指向前一个节点,next指向后一个节点。
2. 带头双向循环链表的实现:
双向链表初始化:
LTNode* InitList()
{
LTNode* phead = BuyList(-1);
phead->next = phead;
phead->prev = phead;
return phead;
}双向循环链表开始时头和尾都指向自己:
BuyList函数的功能是创建节点,我们在初始化时用它创建哨兵位头节点,因为后面还有多次使用,所以把它封装为函数。
双向链表打印:
void Print(LTNode* phead)
{
LTNode*cur = phead->next;
printf("guard<->");
while (cur != phead)
{
printf("%d<->", cur->data);
cur = cur->next;
}
printf("\n");
}开辟节点函数:
LTNode* BuyList(ListDatatype x)
{
LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->prev = NULL;
newnode->next = NULL;
newnode->data = x;
return newnode;
}双向链表头插:
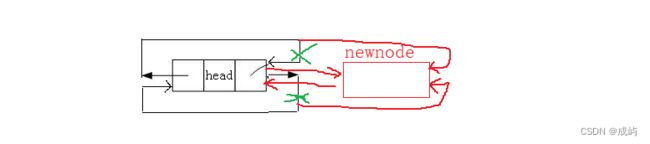
头插实际是在哨兵位头节点phead的后面插入,保存住head->next的位置,然后把newnode前后分别和head、head->next链接起来就行。
代码如下:
void ListPushFront(LTNode* phead, ListDatatype x)
{
assert(phead);
LTNode* newnode = BuyList(x);
LTNode* next = phead->next;
phead->next = newnode;
next->prev = newnode;
newnode->next = next;
newnode->prev = phead;
}这段代码神奇的地方在于,即使链表为空,它也能头插,并且不需要判断链表是否为空:
因为就算链表为空,我们有哨兵位头节点存在,就不用担心空指针的问题。
双向链表尾插:
双向链表相对于单链表的优势就是不用找尾,因为它的phead->prev就是尾,尾插同头插差不多, 把newnode的前后分别和链表的尾和头链接起来即可。
代码如下:
void ListPushBack(LTNode* phead, ListDatatype x)
{
assert(phead);
LTNode* newnode = BuyList(x);
LTNode* tail = phead->prev;
tail->next = newnode;
phead->prev = newnode;
newnode->prev = tail;
newnode->next = phead;
}和头插一样,尾插也不用判断链表为空的情况。
双向链表头删:
头删指的是删除哨兵位头节点后面一个节点,只要将头节点与要删除的节点后面的节点相连接,然后free掉要删除的节点即可。
代码如下:
void ListPopFront(LTNode* phead)
{
assert(phead);
assert(!ListEmpty(phead));
LTNode* cur = phead;
LTNode* first = cur->next;
LTNode* second = first->next;
second->prev = phead;
phead->next = second;
free(first);
}删除时要注意不能删除哨兵位头节点,所以要断言一下,链表为空就不能再删了,我们也可以封装一个判断链表是否为空的函数ListEmpty():
bool ListEmpty(LTNode* phead)
{
assert(phead);
return phead->next == phead;
}bool类型的返回值是true或者false。
双向链表尾删:
尾删要保存尾节点的前一个节点,然后把前一个节点和头节点链接起来,free尾节点即可。
代码如下:
void ListPopBack(LTNode* phead)
{
assert(phead);
assert(!ListEmpty(phead));
LTNode* tail = phead->prev;
LTNode* tailPrev = tail->prev;
tailPrev->next = phead;
phead->prev = tailPrev;
free(tail);
}注意:同头删一样,尾删也要判断是否为空链表。
双向链表查找:
双向循环链表的查找和单链表的查找不同,遍历时从head的下一个节点开始,到head的上一个节点(即尾节点)结束,所以判断条件有所不同,注意区分。找到时,返回该节点位置。
代码如下:
LTNode* ListSearch(LTNode*phead,ListDatatype x)
{
assert(phead);
LTNode* cur = phead->next;
while (cur != phead)
{
if (cur->data == x)
{
return cur;
}
cur = cur->next;
}
return NULL;
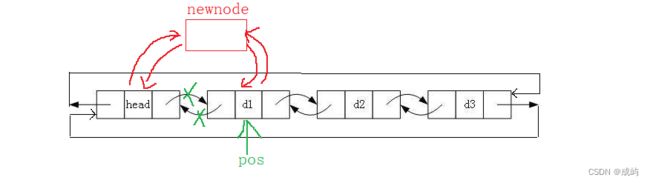
}双向链表在pos之前插入:
保存pos的前一个节点,把newnode的前后分别与pos的前一个节点和pos链接起来即可。
要测试该功能,可以配合查找函数,先找到pos。
代码如下:
void ListInsert(LTNode* pos, ListDatatype x)
{
assert(pos);
LTNode* newnode = BuyList(x);
LTNode* posPrev = pos->prev;
newnode->next = pos;
newnode->prev = posPrev;
posPrev->next = newnode;
pos->prev = newnode;
}这段代码可以直接在头插和尾插中复用,也就是说,我们要实现头插、尾插和任意位置插入,只用这一个函数就可以解决。
头插:
ListInsert(phead->next, x);尾插:
ListInsert(phead, x);
双向链表在pos位置删除:
配合查找函数先找到pos位置,然后删除就行。
代码如下:
void ListErase(LTNode* pos)
{
assert(pos);
LTNode* posPrev = pos->prev;
LTNode* posNext = pos->next;
posPrev->next = posNext;
posNext->prev = posPrev;
free(pos);
}这段代码也可以同时实现头删、尾删和任意位置删除:
头删:
ListErase(phead->next);尾删:
ListErase(phead->prev);
双向链表的销毁:
销毁也是从哨兵位的下一个节点开始,注意每次都要保存要销毁节点的后面一个节点的位置,防止找不到后面的节点,最终要把哨兵位也销毁掉。
代码如下:
void ListDestory(LTNode* phead)
{
assert(phead);
LTNode* cur = phead->next;
while (cur != phead)
{
LTNode* next = cur->next;
free(cur);
cur = next;
}
free(phead);
}以上就是双向链表的全部功能实现,下面给出完整代码:
3.完整代码:
test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"List.h"
//测试
ListTest1()
{
LTNode* plist = InitList();
Print(plist);
//头插
ListPushFront(plist, 1);
ListPushFront(plist, 2);
ListPushFront(plist, 3);
ListPushFront(plist, 4);
Print(plist);
//尾插
ListPushBack(plist, 5);
ListPushBack(plist, 6);
ListPushBack(plist, 7);
ListPushBack(plist, 8);
Print(plist);
//头删
ListPopFront(plist);
ListPopFront(plist);
Print(plist);
//尾删
ListPopBack(plist);
ListPopBack(plist);
Print(plist);
//在pos位置之前插入
LTNode* pos = ListSearch(plist, 1);
if (pos != NULL)
ListInsert(pos, 666);
Print(plist);
//在pos位置删除
pos = ListSearch(plist, 6);
if(pos!=NULL)
ListErase(pos);
Print(plist);
}
int main()
{
ListTest1();
return 0;
}List.h
#pragma once
#include
#include
#include
#include
typedef int ListDatatype;
typedef struct ListNode
{
struct ListNode* prev;
struct ListNode* next;
ListDatatype data;
}LTNode;
//双向链表初始化
LTNode* InitList();
//双向链表打印
void Print(LTNode* phead);
//双向链表头插
void ListPushFront(LTNode* phead, ListDatatype x);
//双向链表尾插
void ListPushBack(LTNode* phead, ListDatatype x);
//双向链表头删
void ListPopFront(LTNode* phead);
//双向链表尾删
void ListPopBack(LTNode* phead);
//双向链表查找
LTNode* ListSearch(LTNode*phead,ListDatatype x);
//在pos位置之前插入
void ListInsert(LTNode*pos, ListDatatype x);
//在pos位置删除
void ListErase(LTNode* pos);
//销毁链表
void ListDestory(LTNode* phead); List.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"List.h"
//开辟节点函数
LTNode* BuyList(ListDatatype x)
{
LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->prev = NULL;
newnode->next = NULL;
newnode->data = x;
return newnode;
}
//双向链表初始化
LTNode* InitList()
{
LTNode* phead = BuyList(-1);
phead->next = phead;
phead->prev = phead;
return phead;
}
//打印函数
void Print(LTNode* phead)
{
LTNode*cur = phead->next;
printf("guard<->");
while (cur != phead)
{
printf("%d<->", cur->data);
cur = cur->next;
}
printf("\n");
}
//双向链表头插
void ListPushFront(LTNode* phead, ListDatatype x)
{
assert(phead);
LTNode* newnode = BuyList(x);
LTNode* next = phead->next;
phead->next = newnode;
next->prev = newnode;
newnode->next = next;
newnode->prev = phead;
/*ListInsert(phead->next, x);*/
}
//双向链表尾插
void ListPushBack(LTNode* phead, ListDatatype x)
{
assert(phead);
LTNode* newnode = BuyList(x);
LTNode* tail = phead->prev;
tail->next = newnode;
phead->prev = newnode;
newnode->prev = tail;
newnode->next = phead;
/*ListInsert(phead, x);*/
}
//判断空链表函数
bool ListEmpty(LTNode* phead)
{
assert(phead);
return phead->next == phead;
}
//双向链表头删
void ListPopFront(LTNode* phead)
{
assert(phead);
assert(!ListEmpty(phead));
LTNode* cur = phead;
LTNode* first = cur->next;
LTNode* second = first->next;
second->prev = phead;
phead->next = second;
free(first);
/*ListErase(phead->next);*/
}
//双向链表尾删
void ListPopBack(LTNode* phead)
{
assert(phead);
assert(!ListEmpty(phead));
LTNode* tail = phead->prev;
LTNode* tailPrev = tail->prev;
tailPrev->next = phead;
phead->prev = tailPrev;
free(tail);
/*ListErase(phead->prev);*/
}
//双向链表查找
LTNode* ListSearch(LTNode*phead,ListDatatype x)
{
assert(phead);
LTNode* cur = phead->next;
while (cur != phead)
{
if (cur->data == x)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
//双向链表在pos之前插入
void ListInsert(LTNode* pos, ListDatatype x)
{
assert(pos);
LTNode* newnode = BuyList(x);
LTNode* posPrev = pos->prev;
newnode->next = pos;
newnode->prev = posPrev;
posPrev->next = newnode;
pos->prev = newnode;
}
//双向链表在pos位置删除
void ListErase(LTNode* pos)
{
assert(pos);
LTNode* posPrev = pos->prev;
LTNode* posNext = pos->next;
posPrev->next = posNext;
posNext->prev = posPrev;
free(pos);
}
//双向链表销毁
void ListDestory(LTNode* phead)
{
assert(phead);
LTNode* cur = phead->next;
while (cur != phead)
{
LTNode* next = cur->next;
free(cur);
cur = next;
}
free(phead);
}4.测试:

5.顺序表和链表的区别
| 不同点 | 顺序表 | 链表 |
| 存储空间上 | 物理上一定连续 | 逻辑上连续,但物理上不一定连续 |
| 随机访问 | 支持O(1) | 不支持:O(N) |
| 任意位置插入或者删除元 素 |
可能需要搬移元素,效率低O(N) | 只需修改指针指向 |
| 插入 | 动态顺序表,空间不够时需要扩 容 |
没有容量的概念 |
| 应用场景 | 元素高效存储+频繁访问 | 任意位置插入和删除频繁 |
| 缓存利用率 | 高 | 低 |
总结一下:
下面我们再来补充一些内容:
这里有个问题,在计算机中使用顺序表效率高还是使用链表效率高呢?
答案是:顺序表。
因为在计算机中,由于运行速度不匹配的问题,CPU不会直接和主存交换数据,而是先把数据从主存中取出来放到高速缓存中,然后再进行访问数据,而访问数据会出现两种情况:
1.如果数据在缓存中,就叫做缓存命中,可以直接访问。
2.如果数据不在缓存中,就叫做缓存不命中,这时候需要先把数据加载到缓存中,然后再访问数据。
当缓存不命中时,计算机会把数据加载到缓存中,而加载时会将这个数据后面的数据也一起加载进去(局部性原理),如果是顺序表,因为它的内存空间是连续的,后面的数据会直接命中,这样它的缓存命中率就高;如果是链表,它一旦命中不了,也会加载一段数据,但是这些数据不一定会用,这就造成了浪费,还会导致数据污染,这样它的缓存命中率就低了。
这就是今天关于双向链表的全部内容了,未完待续。。。