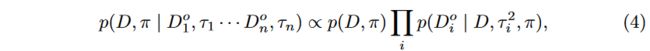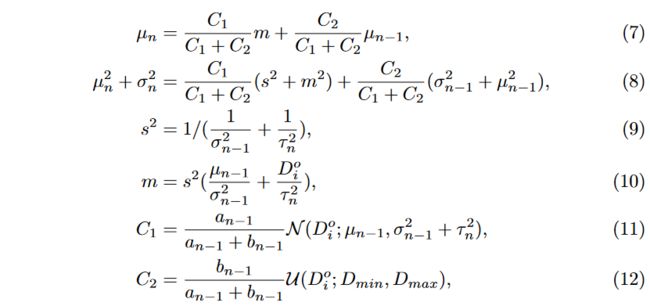【论文阅读】PSDF Fusion:用于动态 3D 数据融合和场景重建的概率符号距离函数
【论文阅读】PSDF Fusion:用于动态 3D 数据融合和场景重建的概率符号距离函数
- Abstract
- 1 Introduction
- 3 Overview
-
- 3.1 Hybrid Data Structure
- 3.2 3D Representations
- 3.3 Pipeline
- 4 PSDF Fusion and Surface Reconstruction
-
- 4.1 PSDF Fusion
- 4.2 Inlier Ratio Evaluation
- 4.3 Surface Extraction
- 5 Experiments
-
- 5.1 Qualitative Results
- 5.2 Quantitative Results
- 6 Conclusions

PSDF Fusion: Probabilistic Signed Distance Function for On-the-fly 3D Data Fusion and Scene Reconstruction
Abstract
We propose a novel 3D spatial representation for data fusion and scene reconstruction. Probabilistic Signed Distance Function (Probabilistic SDF, PSDF) is proposed to depict uncertainties in the 3D space. It is modeled by a joint distribution describing SDF value and its inlier probability, reflecting input data quality and surface geometry. A hybrid data structure involving voxel, surfel, and mesh is designed to fully exploit the advantages of various prevalent 3D representations. Connected by PSDF, these components reasonably cooperate in a consistent framework. Given sequential depth measurements, PSDF can be incrementally refined with less ad hoc parametric Bayesian updating. Supported by PSDF and the efficient 3D data representation, high-quality surfaces can be extracted on-the-fly, and in return contribute to reliable data fusion using the geometry information. Experiments demonstrate that our system reconstructs scenes with higher model quality and lower redundancy, and runs faster than existing online mesh generation systems.
我们提出了一种用于数据融合和场景重建的新颖 3D 空间表示。概率符号距离函数(概率SDF,PSDF)被提出来描述3D空间中的不确定性。它通过描述 SDF 值及其内点概率的联合分布建模,反映输入数据质量和表面几何形状。涉及体素、面元和网格的混合数据结构旨在充分利用各种流行 3D 表示的优势。这些组件通过 PSDF 连接,在一致的框架中合理地协作。给定连续的深度测量,PSDF 可以通过较少的临时参数贝叶斯更新来逐步细化。在 PSDF 和高效 3D 数据表示的支持下,可以即时提取高质量的表面,从而利用几何信息实现可靠的数据融合。实验表明,我们的系统以更高的模型质量和更低的冗余重建场景,并且比现有的在线网格生成系统运行得更快。
1 Introduction
In recent years, we have witnessed the appearance of consumer-level depth sensors and the increasing demand of real-time 3D geometry information in nextgeneration applications. Therefore, online dense scene reconstruction has been a popular research topic. The essence of the problem is to fuse noisy depth data stream into a reliable 3D representation where clean models can be extracted. It is necessary to consider uncertainty in terms of sampling density, measurement accuracy, and surface complexity so as to better understand the 3D space.
Many representations built upon appropriate mathematical models are designed for robust data fusion in such a context. To handle uncertainties, surfel and point based approaches [29,13,15] adopt filtering-based probabilistic models that explicitly manipulate input data. Volume based methods [20,12,5,27], on the other hand, maximize spatial probabilistic distributions and output discretized 3D properties such as SDF and occupancy state. With fixed topologies, mesh based methods [35] may also involve parametric minimization of error functions.
近年来,我们见证了消费级深度传感器的出现以及下一代应用中对实时 3D 几何信息的需求不断增长。因此,在线密集场景重建一直是热门的研究课题。问题的本质是将嘈杂的深度数据流融合到可靠的 3D 表示中,从而可以提取干净的模型。有必要考虑采样密度、测量精度和表面复杂性方面的不确定性,以便更好地理解 3D 空间。
许多基于数学模型的表示都是为了在这种情况下进行稳健的数据融合而设计的。为了处理不确定性,面元和基于点的方法[29,13,15]采用基于过滤的概率模型来显式地操纵输入数据。另一方面,基于体积的方法 [20,12,5,27] 最大化空间概率分布并输出离散 3D 属性,例如 SDF 和占用状态。对于固定拓扑,基于网格的方法[35]也可能涉及误差函数的参数最小化。
While such representations have been proven effective by various applications, their underlying data structures endure more or less drawbacks. Surfels and points are often loosely managed without topology connections, requiring additional modules for efficient indexing and rendering [1], and is relatively prone to noisy input. Volumetric grids lack flexibility to some extent, hence corresponding data fusion can be either oversimplified using weighted average [20], or much time-consuming in order to maximize joint distributions [27]. In addition, ray-casting based volume rendering is also non-trivial. Usually storing vertices with strong topological constraints, mesh is similarly hard to manipulate and is less applicable to many situations. There have been studies incorporating aforementioned data structures [18,24,14,23], yet most of these pipelines are loosely organized without fully taking the advantages of each representation.
虽然这种表示形式已被各种应用程序证明是有效的,但它们的底层数据结构或多或少存在缺陷。面元和点通常是松散管理的,没有拓扑连接,需要额外的模块来进行有效的索引和渲染[1],并且相对容易产生噪声输入。体积网格在某种程度上缺乏灵活性,因此相应的数据融合要么使用加权平均值过于简化[20],要么为了最大化联合分布而耗费大量时间[27]。此外,基于光线投射的体积渲染也很重要。网格通常存储具有强拓扑约束的顶点,同样难以操作并且不太适用于许多情况。已经有研究结合了上述数据结构[18,24,14,23],但大多数这些管道都是松散组织的,没有充分利用每种表示的优点。
In this paper, we design a novel framework to fully exploit the power of existing 3D representations, supported by PSDF-based probabilistic computations. Our framework is able to perform reliable depth data fusion and reconstruct high-quality surfaces in real-time with more details and less noise, as depicted in Fig.1. Our contributions can be concluded as:
1. We present a novel hybrid data structure integrating voxel, surfel, and mesh;
2. The involved 3D representations are systematically incorporated in the consistent probabilistic framework linked by the proposed PSDF;
3. Incremental 3D data fusion is built upon less ad-hoc probabilistic computations in a parametric Bayesian updating fashion, contributes to online surface reconstruction, and benefits from iteratively recovered geometry in return.
在本文中,我们设计了一个新颖的框架,以充分利用现有 3D 表示的能力,并由基于 PSDF 的概率计算支持。我们的框架能够执行可靠的深度数据融合,并实时重建高质量的表面,细节更多,噪声更少,如图 1 所示。我们的贡献可以总结为:
- 我们提出了一种集成体素、面元和网格的新型混合数据结构;
- 所涉及的 3D 表示被系统地纳入所提出的 PSDF 链接的一致概率框架中;
- 增量 3D 数据融合以参数贝叶斯更新方式建立在较少的临时概率计算之上,有助于在线表面重建,并从迭代恢复的几何图形中受益。

图 1.burghers的重建网格。热图表示 SDF 内点比率(SDF 置信度)。注意细节被保留,异常值已被全部删除,无需任何后处理。图 4、5、6 中的内点比热图也符合此颜色条。
2 Related Work
3 Overview
Our framework is based on the hybrid data structure involving three 3D representations linked by PSDF. The pipeline consists of iterative operations of data fusion and surface generation.
我们的框架基于混合数据结构,涉及由 PSDF 链接的三个 3D 表示。该管道由数据融合和表面生成的迭代操作组成。
3.1 Hybrid Data Structure
We follow [22,14,6] and use a spatial hashing based structure to efficiently manage the space. A hash entry would point to a block, which is the smallest unit to allocate and free. A block is further divided into 8 × 8 × 8 small voxels. Following [6] we consider a voxel as a 3-edge structure instead of merely a cube, as depicted in Fig.2(a), which will avoid ambiguity when we refer to shared edges. PSDF values are stored at the corners of these structures. In addition, we maintain surfels on the volumetric grids by limiting their degree of freedom on the edges of voxels; within a voxel at most 3 surfels on edges could be allocated. This constraint would regularize the distribution of surfels, guarantee easier access, and avoid duplicate allocation. Triangles are loosely organized in the level of blocks, linking adjacent surfels. In the context of mesh, a surfel could be also interpreted as a triangle vertex.
我们遵循[22,14,6]并使用基于空间哈希的结构来有效地管理空间。哈希条目将指向一个块,这是分配和释放的最小单元。一个块被进一步分为 8 × 8 × 8 个小体素。在[6]之后,我们将体素视为3边结构,而不仅仅是一个立方体,如图2(a)所示,这将避免当我们引用共享边时产生歧义。 PSDF 值存储在这些结构的拐角处。此外,我们通过限制体素边缘的自由度来维持体积网格上的面元;在一个体素内最多可以分配边缘上的 3 个面元。此约束将规范面元的分布,保证更容易访问,并避免重复分配。三角形在块的水平上松散地组织,连接相邻的面元。在网格的上下文中,面元也可以解释为三角形顶点。
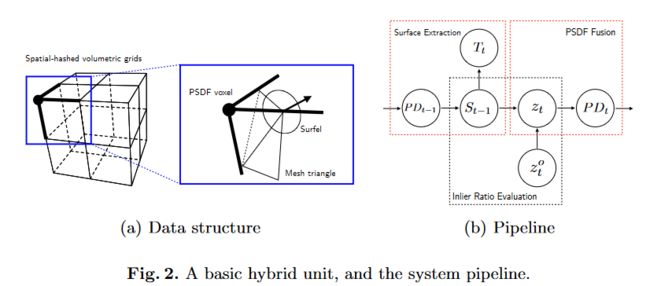
图 2. 基本混合单元和系统管道。
3.2 3D Representations
Voxel and PSDF.
In most volumetric reconstruction systems SDF or truncated SDF (TSDF) (denoted by D) of a voxel is updated when observed 3D points fall in its neighbor region. Projective signed distances from measurements, which could be explained as SDF observations, are integrated by computing weight average. Newcombe [19] suggests that it can be regarded as the solution of a maximum likelihood estimate of a joint Gaussian distribution taking SDF as a random variable. While Gaussian distribution could depict the uncertainty of data noise, it might fail to handle outlier inputs which are common in reconstruction tasks using consumer-level sensors. Moreover, SDF should depict the projective distance from a voxel to its closest surface. During integration, however, it is likely that non-closest surface points are taken into account, which should also be regarded as outlier SDF observations. In view of this, we introduce another random variable π π π to denote the inlier ratio of SDF, initially used in [29] to model the inlier ratio of 3D points:
在大多数体积重建系统中,当观察到的 3D 点落入其邻近区域时,SDF 或截断 SDF (TSDF)(用 D 表示)就会更新。测量的投影有符号距离(可以解释为 SDF 观测值)通过计算权重平均值进行积分。 Newcombe [19]认为它可以被视为以 SDF 作为随机变量的联合高斯分布的最大似然估计的解。虽然高斯分布可以描述数据噪声的不确定性,但它可能无法处理使用消费者级传感器的重建任务中常见的异常输入。此外,SDF 应该描述从体素到其最近表面的投影距离。然而,在积分过程中,很可能会考虑非最近的表面点,这也应被视为离群 SDF 观测值。鉴于此,我们引入另一个随机变量 π π π 来表示 SDF 的内点比率,最初在[29]中用于建模 3D 点的内点比率:
![]()
where D i o D^o_i Dio reads an SDF observation computed with depth measurements, τ i τ_i τi is the variance of the SDF observation, N N N and U U U are Gaussian and Uniform distributions.
其中 D i o D^o_i Dio 读取通过深度测量计算的 SDF 观测值, τ i τ_i τi 是 SDF 观测值的方差, N N N 和 U U U 是高斯分布和均匀分布。
Following [29], the posterior of PSDF can be parameterized by a Beta distribution multiplying a Gaussian distribution B ( a , b ) N ( μ ; σ 2 ) B(a, b)N (μ; σ^2) B(a,b)N(μ;σ2), given a series of observed input SDF measurements. The details will be discussed in §4.1. The parameters a , b , μ , σ a, b, μ, σ a,b,μ,σ of the parameterized distribution are maintained per voxel.
根据[29],在给定一系列观察到的输入 SDF 测量值的情况下,PSDF 的后验可以通过 Beta 分布乘以高斯分布 B ( a , b ) N ( μ ; σ 2 ) B(a, b)N (μ; σ^2) B(a,b)N(μ;σ2) 进行参数化。详细信息将在第 4.1 节中讨论。每个体素都保留参数化分布的参数 a , b , μ , σ a, b, μ, σ a,b,μ,σ 。
Surfel.
A surfel in our pipeline is formally defined by a position x x x, a normal n n n, and a radius r r r. Since a certain surfel is constrained on an edge in the volume, x x x is generally an interpolation of 2 adjacent voxel corners.
面元
我们管道中的面元由位置 x x x、法线 n n n 和半径 r r r 定义。由于某个面元被约束在体积中的边缘上,因此 x x x 通常是 2 个相邻体素角的插值。

图 3. 左图显示具有多个 SDF 观测值的 PSDF 分布( D 1 o D^o_1 D1o 可能是内值观测值, D 2 o D^o_2 D2o 可能是离群值)。红色曲线显示每个观察值的高斯分布。蓝色曲线描绘了 Beta 分布,直观地表明内点观测值应该在 D 1 o D^o_1 D1o 附近。右图是涉及观测到的输入 3D 点和已知面元的 SDF 内点比率 ρ 的估计。
Triangle.
A triangle consists of 3 edges, each linking two adjacent surfels. These surfels can be located in different voxels, even different blocks. In our framework triangles are mainly extracted for rendering; the contained topology information may be further utilized in extensions.
三角形
三角形由 3 条边组成,每条边连接两个相邻的面元。这些面元可以位于不同的体素,甚至不同的块中。在我们的框架中,主要提取三角形用于渲染;所包含的拓扑信息可以进一步在扩展中使用。
Depth input.
We receive depth measurements from sensors as input, while sensor poses are assumed known. Each observed input depth zo is modeled as a random variable subject to a simple Gaussian distribution:
深度输入
我们接收来自传感器的深度测量值作为输入,同时假设传感器姿态已知。每个观察到的输入深度 z o z^o zo 都被建模为服从简单高斯分布的随机变量:
![]()
where ι ι ι can be estimated from a precomputed sensor error model.
其中 ι ι ι 可以根据预先计算的传感器误差模型进行估计。
3.3 Pipeline
In general, our system will first generate a set of surfels S t − 1 S_{t−1} St−1 in the volumetric PSDF field P D t − 1 PD_{t−1} PDt−1. Meanwhile, mesh triangle set T t T_t Tt is also determined by linking reliable surfels in S t − 1 S_{t−1} St−1. S t − 1 S_{t−1} St−1 explicitly defines the surfaces of the scene, hence can be treated as a trustworthy geometry cue to estimate outlier ratio of the input depth data z t o z^o_t zto . P D t − 1 PD_{t−1} PDt−1 is then updated to P D t PD_{t} PDt by fusing evaluated depth data distribution z t z_t zt via Bayesian updating. The process will be performed iteratively every time input data come, as depicted in Fig.2(b). We assume the poses of the sensors are known and all the computations are in the world coordinate system.
一般来说,我们的系统将首先在体积 PSDF 场 P D t − 1 P Dt−1 PDt−1 中生成一组面元 S t − 1 S_{t−1} St−1。同时,网格三角形集合 T t T_t Tt 也是通过链接 S t − 1 S_{t−1} St−1中的可靠面元来确定的。 S t − 1 S_{t−1} St−1 明确定义了场景的表面,因此可以被视为可靠的几何线索来估计输入深度数据 z t o z^o_t zto的异常值比率。然后通过贝叶斯更新融合评估的深度数据分布 z t z_t zt,将 P D t − 1 PD_{t−1} PDt−1 更新为 P D t PD_{t} PDt。每次输入数据到来时,该过程都会迭代执行,如图2(b)所示。我们假设传感器的位姿已知,并且所有计算都在世界坐标系中进行。
4 PSDF Fusion and Surface Reconstruction
4.1 PSDF Fusion
Similar to [20], in order to get SDF observations of a voxel V V V given input 3D points from depth images, we first project V V V to the depth image to find the projective closest depth measurement z i z_i zi. Signed distance from V to the input 3D data is defined by
与[20]类似,为了获得给定深度图像输入3D点的体素V的SDF观测值,我们首先将 V V V 投影到深度图像以找到投影最接近的深度测量 z i z_i zi。从 V V V 到输入 3D 数据的有符号距离定义为
![]()
where z V z^V zV is a constant value, the projective depth of V along the scanning ray.
其中 z V z^V zV是一个常数值,即 V V V沿扫描射线的投影深度。
The observed D i o D^o_i Dio is affected by the variance ι i ι_i ιi of z i z_i zi in Eq.2 contributing to the Gaussian distribution component in Eq.1, provided D i D_i Di is an inlier. Otherwise, D i D_i Di would be counted in the uniform distribution part. Fig.3(a) illustrates the possible observations of SDF in one voxel.
Variance ι i ι_i ιi can be directly estimated by pre-measured sensor priors such as proposed in [21]. In this case, due to the simple linear form in Eq.3, we can directly set D i o = z i o − z V D^o_i= z^o_i− z^V Dio=zio−zV and τ i = ι i τ_i = ι_i τi=ιi in Eq.1.
Given a series of independent observations D i o D^o_i Dio, we can derive the posterior
假设 D i D_i Di 是内点,观测到的 D i o D^o_i Dio会受到方程 2 中 z i z_i zi 的方差 ι i ι_i ιi 的影响,该方差对方程 1 中的高斯分布分量有贡献。否则, D i D_i Di将被计入均匀分布部分。图 3(a) 说明了一个体素中 SDF 的可能观察结果。
方差 ι i ι_i ιi可以通过预先测量的传感器先验直接估计,如[21]中提出的。在这种情况下,由于方程3中的简单线性形式,我们可以直接在方程1中设置 D i o = z i o − z V D^o_i= z^o_i− z^V Dio=zio−zV和 τ i = ι i τ_i = ι_i τi=ιi。
给定一系列独立观察 D i o D^o_i Dio ,我们可以得出后验
where p ( D , π ) p(D, π) p(D,π) is a prior and p ( D i o ∣ D , τ i 2 , π ) p(D^o_i | D, τ^2_i , π) p(Dio∣D,τi2,π) is defined by Eq.1. It would be intractable to evaluate the production of such distributions with additions. Fortunately, [29] proved that the posterior could be approximated by a parametric joint distribution:
其中 p ( D , π ) p(D, π) p(D,π) 是先验, p ( D i o ∣ D , τ i 2 , π ) p(D^o_i | D, τ^2_i , π) p(Dio∣D,τi2,π) 由方程 1 定义。要评估这种有附加值的分布是很困难的。幸运的是,[29]证明后验可以通过参数联合分布来近似:
![]()
therefore the problem could be simplified as a parameter estimation in an incremental fashion:
因此,问题可以简化为增量方式的参数估计:
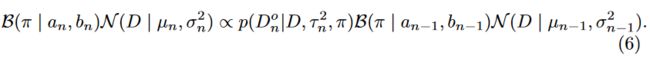
In [29] by equating first and second moments of the random variables π π π and D D D, the parameters could be easily updated, in our case evoking the change of SDF distribution and its inlier probability:
在 [29] 中,通过等效随机变量 π π π 和 D D D 的第一矩和第二矩,可以很容易地更新参数,在我们的案例中,引起了 SDF 分布及其异常值概率的变化::
the computation of a a a and b b b are the same as [29] hence ignored here. In our experiments we find that a truncated D i o D^o_i Dio leads to better results, as it directly rejects distant outliers. SDF observations from non-closest surfaces are left to be handled by PSDF.
a a a 和 b b b 的计算与[29]相同,因此这里忽略。在我们的实验中,我们发现截断的 D i o D^o_i Dio 会带来更好的结果,因为它直接拒绝远处的异常值。来自非最近表面的 SDF 观测结果由 PSDF 处理。
4.2 Inlier Ratio Evaluation
In Eq.11-12, the expectation of B ( π ∣ a , b ) B(π | a, b) B(π∣a,b) is used to update the coefficients, failing to make full use of known geometry properties in scenes. In our pipeline, available surface geometry is considered to evaluate the inlier ratio ρ n ρ_n ρn of D n o D^o_n Dno, replacing the simple a n − 1 a n − 1 + b n − 1 \frac{a_{n−1}}{a_{n−1}+b_{n−1}} an−1+bn−1an−1 . Note ρ n ρ_n ρn is computed per-frame in order to update C 1 , C 2 C_1, C_2 C1,C2; π π π is still parameterized by a a a and b b b.
式11-12中,利用 B ( π ∣ a , b ) B(π | a, b) B(π∣a,b) 的期望来更新系数,未能充分利用场景中已知的几何特性。在我们的流程中,考虑可用的表面几何形状来评估 D n o D^o_n Dno 的内点比率 ρ n ρ_n ρn ,取代简单的 a n − 1 a n − 1 + b n − 1 \frac{a_{n−1}}{a_{n−1}+b_{n−1}} an−1+bn−1an−1 。注意 ρ n ρ_n ρn 是逐帧计算的,以便更新 C 1 、 C 2 C_1、 C_2 C1、C2; π π π 仍然由 a a a 和 b b b 参数化。
ρ n ρ_n ρn can be determined by whether an input point z z z is near the closest surface of a voxel and results in an inlier SDF observation. We first cast the scanning ray into the volume and collect the surfels maintained on the voxels hit by the ray. Given the surfels, 3 heuristics are used, as illustrated in Fig.3(b).
ρ n ρ_n ρn可以通过输入点 z z z 是否靠近体素的最近表面以及是否会产生离群 SDF 观察结果来确定。首先,我们将扫描射线投射到体量中,然后收集射线击中的体素上的曲面。如图 3(b)所示,我们使用了 3 种启发式方法。
Projective distance.
This factor is used to measure whether a sampled point is close enough to a surfel which is assumed the nearest surface to the voxel:
投影距离
该因子用于测量采样点是否足够接近面元,该面元被假定为距离体素最近的表面:

where v v v is the normalized direction of the ray in world coordinate system and θ θ θ is a preset parameter proportional to the voxel resolution.
其中 v v v 是世界坐标系中光线的归一化方向, θ θ θ 是与体素分辨率成比例的预设参数。
Angle.
Apart from projective distance, we consider angle as another factor, delineating the possibility that a scanning ray will hit a surfel. We use the empirical angle weight in [15]:
角度
除了投影距离外,我们还将角度作为另一个因素来考虑,因为角度决定了扫描光线击中曲面的可能性。我们使用 [15] 中的经验角度权重::
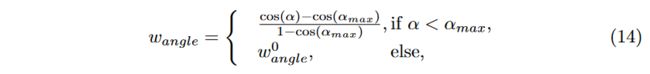
where α = 〈 n , v 〉 α = 〈n, v〉 α=〈n,v〉, α m a x α_{max} αmax is set to 80 deg and w a n g l e 0 w^0_{angle} wangle0 assigned to 0.1.
其中 α = 〈 n , v 〉 α = 〈n, v〉 α=〈n,v〉, α m a x α_{max} αmax 设置为 80 度, w a n g l e 0 w^0_{angle} wangle0 角度指定为 0.1。
Radius.
The area that surfels could influence vary, due to the local shape of the surface. The further a point is away from the center of a surfel, the less possible it would be supported. A sigmoid-like function is used to encourage a smooth transition of the weight:
半径
由于曲面的局部形状不同,面元所能影响的区域也不同。一个点离面元中心越远,它获得支持的可能性就越小。为了使权重平稳过渡,我们使用了一个类似于 sigmoid 的函数:
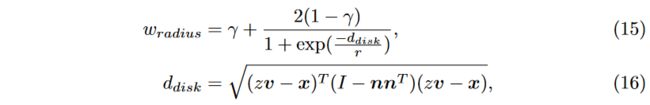
where parameter γ ∈ [ 0 , 1 ) γ ∈ [0, 1) γ∈[0,1) and is set to 0.5 in our case.
Putting all the factors together, we now have
其中参数 γ ∈ [ 0 , 1 ) γ ∈ [0, 1) γ∈[0,1) 在我们的例子中设置为 0.5。
将所有因素放在一起,我们现在有
![]()
To compute the ρ ρ ρ predicted by all the surfels, one may consider either summations or multiplications. However, we choose the highest ρ ρ ρ instead – intuitively a depth measurement is a sample on a surface, corresponding to exactly one surfel. A more sophisticated selection might include a ray consistency evaluation [32,27,28] where occlusion is handled. When a new area is explored where no surfels have been extracted, we use a constant value ρ p r = 0.1 ρ_{pr} = 0.1 ρpr=0.1 to represent a simple occupancy prior in space, hence we have
为了计算所有面元预测的 ρ ρ ρ,可以考虑求和或乘法。然而,我们选择最高的 ρ ρ ρ ——直观上,深度测量是表面上的样本,恰好对应于一个面元。更复杂的选择可能包括光线一致性评估[32,27,28],其中会对遮挡进行处理。当探索未提取面元的新区域时,我们使用常数值 ρ p r = 0.1 ρ_{pr} = 0.1 ρpr=0.1 来表示空间中的简单占用先验,因此我们有
![]()
4.3 Surface Extraction
PSDF implicitly defines zero crossing surfaces and decides whether they are true surfaces. The surface extraction is divided into two steps.
PSDF 隐式定义零交叉曲面并决定它们是否为真实曲面。表面提取分为两个步骤。
Surfel generation.
In this stage we enumerate zero-crossing points upon 3 edges of each voxel and generate surfels when condition are satisfied,
面元生成
在此阶段,我们枚举每个体素 3 个边缘上的零交叉点,并在以下条件满足时生成面元
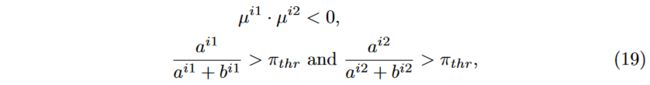
where i 1 i1 i1 and i 2 i2 i2 are indices of adjacent voxels and π t h r π_{thr} πthr is a confidence threshold. Supported by the reliable update of the PSDF, false surfaces could be rejected and duplicates could be removed. According to our experiments, our framework is not sensitive to π t h r π_{thr} πthr; 0.4 would work for all the testing scenes. A surfel’s position x x x would be the linear interpolation of corresponding voxels’ positions x i x^i xi indexed by i i i, and the radius would be determined by σ σ σ of adjacent voxels, simulating its affecting area. Normal is set to normalized gradient of the SDF field, as mentioned in [20].
其中 i 1 i1 i1 和 i 2 i2 i2 是相邻体素的索引, π t h r π_{thr} πthr 是置信度阈值。在 PSDF 可靠更新的支持下,可以抑制错误表面并删除重复表面。根据我们的实验,我们的框架对 π t h r π_{thr} πthr 不敏感; 0.4 适用于所有测试场景。面元的位置 x x x 将是由 i i i 索引的相应体素位置 x i x^i xi 的线性插值,半径将由相邻体素的 σ σ σ 确定,模拟其影响区域。法线设置为 SDF 场的归一化梯度,如[20]中所述。
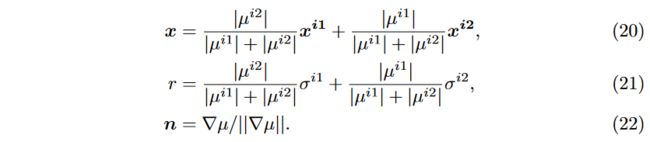
Triangle generation.
Having sufficient geometry information within surfels, there is only one more step to go for rendering-ready mesh. The connections between adjacent surfels are determined by the classical MarchingCubes [17] method. As a simple modification, we reject edges in the voxel whose σ σ σ is larger than a preset parameter σ t h r σ_{thr} σthr. This operation will improve the visual quality of reconstructed model while preserving surfels for the prediction stage.
三角形生成
有了曲面内足够的几何信息,只需再进行一个步骤就可以得到可渲染的网格了。相邻曲面之间的连接由经典的 MarchingCubes [17] 方法确定。作为一个简单的修改,我们会剔除体素中 σ σ σ 大于预设参数 σ t h r σ_{thr} σthr 的边。这一操作将提高重建模型的视觉质量,同时为预测阶段保留曲面。
5 Experiments
We test our framework (denoted by PSDF) on three RGB-D datasets: TUM [25], ICL-NUIM [9], and dataset from Zhou and Koltun [34]. Our method is compared against [6] (denoted by TSDF ) which incrementally extracts mesh in spatial-hashed TSDF volumes. The sensors’ poses are assumed known for these datasets, therefore the results of TSDF should be similar to other stateof-the-art methods such as [22,23] where TSDF integration strategies are the same. We demonstrate that our method reconstructs high quality surfaces by both qualitative and quantitative results. Details are preserved while noise is removed in the output models. The running speed for online mesh extraction is also improved by avoiding computations on false surfel candidates.
我们在三个 RGB-D 数据集上测试我们的框架(用 PSDF 表示):TUM [25]、ICL-NUIM [9] 以及来自 Zhou 和 Koltun 的数据集 [34]。我们的方法与 [6](由 TSDF 表示)进行比较,后者增量地提取空间哈希 TSDF 体积中的网格。假设这些数据集的传感器姿态已知,因此 TSDF 的结果应该与其他最先进的方法类似,例如 [22,23],其中 TSDF 集成策略是相同的。我们证明我们的方法通过定性和定量结果重建高质量的表面。保留细节,同时消除输出模型中的噪声。通过避免对虚假面元候选的计算,还提高了在线网格提取的运行速度。
For [25,34] we choose a voxel size of 8mm and σ t h r σ_{thr} σthr= 16mm; for [9] voxel size is set to 12mm and σ t h r σ_{thr} σthr = 48mm. The truncation distance is set to 3× voxel size plus 3 × τ τ τ ; with a smaller truncation distance we found strides and holes in meshes. Kinect’s error model [21] was adopted to get ι ι ι where the factor of angle was removed, which we think might cause double counting considering wangle in the inlier prediction stage. The program is written in C++/CUDA 8.0 and runs on a laptop with an Intel i7-6700 CPU and an NVIDIA 1070 graphics card.
对于[25,34],我们选择体素大小为 8mm, σ t h r σ_{thr} σthr = 16mm;对于[9],体素大小设置为 12mm, σ t h r σ_{thr} σthr = 48mm。截断距离设置为 3× 体素大小加上 3 × τ τ τ ;使用较小的截断距离,我们在网格中发现了裂缝和孔洞。采用Kinect的误差模型[21]来得到 ι ι ι,其中去除了角度因素,我们认为考虑到内点预测阶段的角度,这可能会导致重复计算。该程序采用 C++/CUDA 8.0 编写,在配备 Intel i7-6700 CPU 和 NVIDIA 1070 显卡的笔记本电脑上运行。
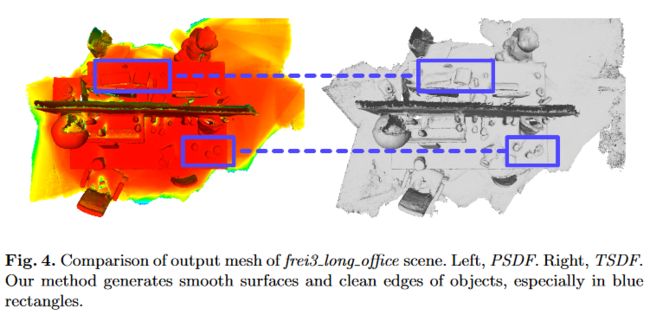
图4. frei3 long office 场景输出网格对比。左,PSDF。右,TSDF。我们的方法生成对象的光滑表面和干净的边缘,特别是在蓝色矩形中。
5.1 Qualitative Results
We first show that PSDF accompanied by the related mesh extraction algorithm produces higher quality surfaces than TSDF. Our results are displayed with shaded heatmap whose color indicates the inlier ratio of related SDF. Both geometry and probability properties can be viewed in such a representation.
我们首先证明 PSDF 结合相关的网格提取算法可以产生比 TSDF 更高质量的表面。我们的结果以阴影热图显示,其颜色表示相关 SDF 的内点比率。几何和概率属性都可以在这样的表示中查看。
Fig.4 shows that PSDF outperforms TSDF by generating clean boundaries of small objects and rejecting noisy areas on the ground. In Fig.5, in addition to the results of TSDF, we also display the reconstructed mesh from offline methods provided by [34] as references. It appears that our method produces results very similar to [34]. While guaranteeing well-covered reconstruction of scenes, we filter outliers and preserve details. In copyroom, the wires are completely reconstructed, one of which above PC is smoothed out in [34] and only partially recovered by TSDF. In lounge, we can observe a complete shape of table, and de-noised details in the clothes.
图 4 显示 PSDF 通过生成小物体的清晰边界并拒绝地面上的噪声区域而优于 TSDF。在图5中,除了TSDF的结果之外,我们还显示了[34]提供的离线方法的重建网格作为参考。看来我们的方法产生的结果与[34]非常相似。在保证场景重建得到良好覆盖的同时,我们过滤异常值并保留细节。在copyroom中,电线被完全重建,其中 PC 上方的电线在[34]中被平滑,并且仅由 TSDF 部分恢复。在lounge,我们可以观察到桌子的完整形状,以及衣服上的去噪细节。
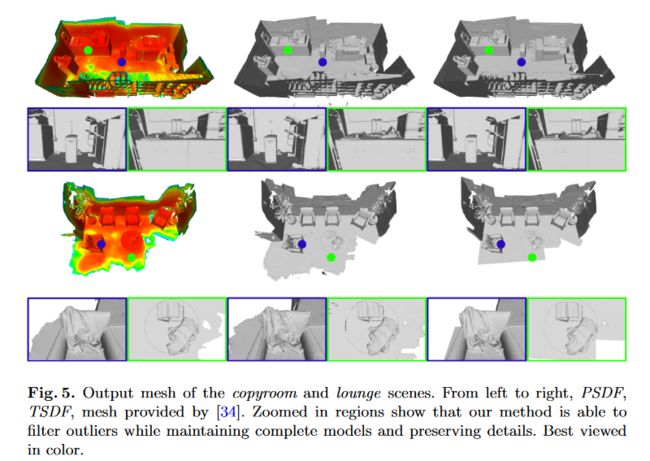
图 5. copyroom和lounge场景的输出网格。从左到右,PSDF、TSDF、网格由[34]提供。放大区域表明我们的方法能够过滤异常值,同时保持完整的模型并保留细节。最好以彩色形式观看。
We also visualize the incremental update of π π π by rendering E ( β ( π ∣ a , b ) ) = a / ( a + b ) E(β(π|a, b)) = a/(a + b) E(β(π∣a,b))=a/(a+b) as the inlier ratio of reconstructed mesh in sequence using colored heatmap. Fig.6 shows the fluctuation of confidence around surfaces. The complex regions such as fingers and wrinkles on statues are more prone to noise, therefore apparent change of shape along with color can be observed.
我们还通过使用彩色热图按顺序将 E ( β ( π ∣ a , b ) ) = a / ( a + b ) E(β(π|a, b)) = a/(a + b) E(β(π∣a,b))=a/(a+b) 渲染为重建网格的内点比率来可视化 π π π 的增量更新。图 6 显示了表面周围置信度的波动。雕像上的手指和皱纹等复杂区域更容易出现噪点,因此可以观察到形状和颜色的明显变化。

图 6. burghers 数据集的增量重建。可以在容易出错的区域观察到概率波动,作为不确定性传播的指示。
5.2 Quantitative Results
Reconstruction Accuracy.
We reconstruct mesh of the synthetic dataset livingroom2 with added noise whose error model is presented in [9]. Gaussian noise on inverse depth plus local offsets is too complicated for our error model, therefore we simplify it by assigning inverse sigma at certain inverse depths to ι i ι_i ιi. The mesh vertices are compared with the ground truth point cloud using the free software CloudCompare [3].
重建精度
我们对合成数据集 livingroom2 的网格进行了重建,并添加了噪声,其误差模型见 [9]。反演深度上的高斯噪声加上局部偏移对于我们的误差模型来说过于复杂,因此我们通过将特定反演深度上的反演 sigma 赋值给 ι i ι_i ιi 来简化误差模型。使用免费软件 CloudCompare [3],将网格顶点与地面真实点云进行比较。
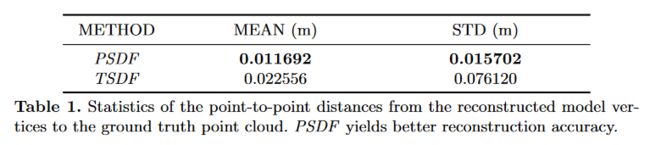
Table.1 indicates that PSDF reconstructs better models than TSDF. Further details in Fig.7 suggest that less outliers appear in the model reconstructed by PSDF, leading to cleaner surfaces.
表 1 表明 PSDF 重建的模型比 TSDF 更好。图 7 中的更多细节表明 PSDF 重建的模型中出现的异常值较少,表面更干净。
表 1 重建模型顶点到地面真实点云的点对点距离统计。 PSDF 产生更好的重建精度。

图 7. PSDF 和 TSDF 的输出网格质量比较。第一行:从重建模型到GT的点对点距离的热图。注意红色矩形中的异常值。第二行,到地面实况的距离分布。将分布分为两部分,以强调 TSDF 重建过程中异常值的存在,而 PSDF 则不会面临此类问题。最好以彩色形式观看。
Mesh size.
Our method maintains the simplicity of mesh by reducing false surface candidates caused by noise and outliers. As shown in Fig.8 and Table 2, PSDF in most cases generates less vertices (% 20) than TSDF, most of which are outliers and boundaries with low confidence. Fig.8 shows that the vertex count remains approximately constant when a loop closure occurred in frei3 long office, while the increasing rate is strictly constrained in the lounge sequence where there is no loop closure.
网格尺寸
我们的方法通过减少由噪声和异常值引起的虚假表面候选来保持网格的简单性。如图 8 和表 2 所示,大多数情况下 PSDF 生成的顶点数量比 TSDF 少(% 20),其中大部分是离群点和置信度较低的边界。图8表明,当 frei3 long office 中发生环路闭合时,顶点数保持近似恒定,而在没有环路闭合的 lounge 序列中,增加率受到严格限制。

图 8. (a)-(b),网格顶点(面元)的增加趋势。 (a),frei3 long office 场景,其中在 1500 帧左右发生循环闭合。 (b),没有循环闭合的lounge 场景。 PSDF 生成的网格消耗了 TSDF 大约 80% 的内存。 ( c)-(f),我们的方法的运行时间分析以及lounge 场景中的比较方法。由于额外的内点预测阶段,PSDF 在 GPU 上慢了 1 毫秒,但会节省更多表面提取时间,总体上速度更快。在线网格划分的速度比光线投射慢,但相当。
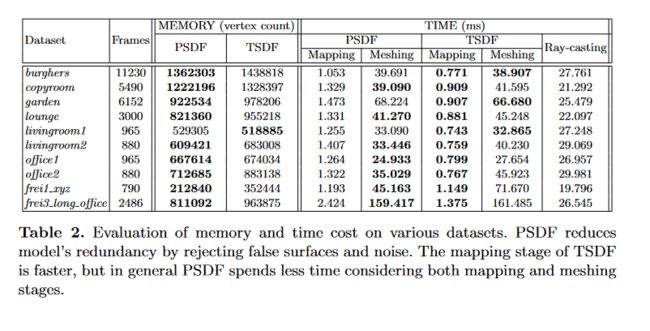
表 2. 各种数据集上的内存和时间成本评估。 PSDF 通过拒绝虚假表面和噪声来减少模型的冗余。 TSDF 的映射阶段速度更快,但一般来说 PSDF 考虑映射和网格划分阶段花费的时间较少。
Time.
To make a running time analysis, we take real world lounge as a typical sequence where noise is common while the camera trajectory fits scanning behavior of humans. As we have discussed, evaluation of inlier ratio was performed, increasing total time of the fusion stage. However we find on a GPU, even with a relatively high resolution, the average increased time is at the scale of ms (see Fig.8( c) and Table.2) and can be accepted. When we come to meshing, we find that by taking the advantage of PSDF fusion and inlier ratio evaluation, unnecessary computations can be avoided and PSDF method runs faster than TSDF, as plotted in Fig.8(d). The meshing stage is the runtime bottleneck of the approach, in general the saved time compensate for the cost in fusion stage, see Fig.8(e) and Table.2. We also compare the time of meshing to the widely used ray-casting that renders surfaces in real-time. According to Table 2, in some scenes where sensor is close to the surfaces performing scanning, less blocks are allocated in viewing frustum and the meshing speed could be comparative to ray-casting, as illustrated in Fig.8(f). As for other scenes requiring a large scanning range, especially frei3 long office where more blocks in frustum have to be processed, ray-casting shows its advantage. We argue that in applications that only require visualization, ray-casting can be adopted; otherwise meshing offers more information and is still preferable.
时间
为了进行运行时间分析,我们将现实世界的lounge 作为一个典型的序列,其中噪声很常见,而相机轨迹符合人类的扫描行为。正如我们所讨论的,进行了内点比率的评估,增加了融合阶段的总时间。然而我们发现在GPU上,即使具有相对较高的分辨率,平均增加的时间也在ms的量级(见图8(c)和表2)并且可以接受。
当我们进行网格划分时,我们发现通过利用 PSDF 融合和内点比率评估的优势,可以避免不必要的计算,并且 PSDF 方法比 TSDF 运行得更快,如图 8(d)所示。网格划分阶段是该方法的运行时瓶颈,一般来说节省的时间补偿了融合阶段的成本,见图8(e)和表2。
我们还将网格划分时间与广泛使用的实时渲染表面的光线投射时间进行了比较。根据表2,在一些传感器靠近执行扫描的表面的场景中,在视锥体中分配较少的块,并且网格划分速度可以与射线投射相当,如图8(f)所示。对于其他需要大扫描范围的场景,特别是 frei3 long office,需要处理更多的视锥体块,光线投射就显示出了它的优势。我们认为,在只需要可视化的应用中,可以采用光线投射;否则,网格划分可以提供更多信息,并且仍然是更好的选择。
6 Conclusions
We propose PSDF, a joint probabilistic distribution to model the spatial uncertainties and 3D geometries. With the help of Bayesian updating, parameters of such a distribution could be incrementally estimated by measuring the quality of input depth data. Built upon a hybrid data structure, our framework can iteratively generate surfaces from the volumetric PSDF field and update PSDF values through reliable probabilistic data fusion supported by reconstructed surfaces. As an output, high-quality mesh can be generated on-the-fly in real-time with duplicates removed and noise cleared.
In the future we intend to extend our framework upon the basis of PSDF. We plan to establish a hierarchical data structure so that the resolution of spatialhashed blocks could be adaptive to input data according to PSDF distributions. We also work on employing more priors to further enrich PSDF probability distributions. Localization modules using the proposed 3D representation are also planned to be integrated in our framework, in order to construct a complete probabilistic SLAM system.
我们提出 PSDF,一种联合概率分布,用于对空间不确定性和 3D 几何进行建模。借助贝叶斯更新,可以通过测量输入深度数据的质量来增量估计这种分布的参数。我们的框架建立在混合数据结构的基础上,可以从体积 PSDF 场迭代生成表面,并通过重建表面支持的可靠概率数据融合来更新 PSDF 值。作为输出,可以实时生成高质量网格,并删除重复项和清除噪声。
未来我们打算在 PSDF 的基础上扩展我们的框架。我们计划建立一个分层数据结构,以便空间散列块的分辨率可以根据 PSDF 分布自适应输入数据。我们还致力于采用更多先验来进一步丰富 PSDF 概率分布。使用所提出的 3D 表示的定位模块也计划集成到我们的框架中,以构建完整的概率 SLAM 系统。
抛砖:
- “PSDF,一种联合概率分布,用于对空间不确定性和 3D 几何进行建模。”—— 这正是目前各类3D重建方法想做到的,尤其是不确定评估这块儿,很多现有方法都要通过GT数据进行评估,当然这是最可靠的评估手段。但是GT数据不总已知,且很多真实场景的GT数据也是通过激光扫描或其他手段获取的,虽然可以视为GT,但真能做到GT吗,显然未必。
- “使用基于空间哈希的结构来有效地管理空间。”
- “将体素视为3边结构,而不仅仅是一个立方体,这将避免当我们引用共享边时产生歧义。”
- 是否可以通过深度学习的方式来构建PSDF呢?目前似乎没有看到相关工作。TSDF倒是有做了的。
- 此文是2018年的工作(可惜没有开源,不然还真想试试看效果如何),应该有不少相关跟进工作,可以跟踪跟踪。