数据结构——顺序表
文章目录
-
- 前言
- 顺序表的定义
- 顺序表的基本运算
-
- 1、顺序表的初始化
- 2、求顺序表的长度
- 3、插入
- 4、删除
- 5、取数据元素
- 6、查找
- 7、遍历
- 顺序表的应用
- 顺序表资源下载(免费哒!)
前言
- 喜欢简单粗暴运行代码来理解顺序表的朋友请点击数据结构-顺序表,下载资源运行代码。
- 想要了解顺序表基础知识,再运行代码来理解的朋友可以先看完我这篇文章的内容再下载资源运行代码。
【注意:数据结构-顺序表这个资源内有完整可执行代码,是免费的!!!支持白嫖修改哈!!!】
!!!废话不多说,进入主题——>顺序表
顺序表的定义
线性表的顺序存储结构是指将线性表的所有数据元素,按其逻辑顺序依次存储在一组连续的内存单元中,用这种存储形式存储的线性表称为顺序表。
其特点是:逻辑关系相邻的两个数据元素在物理位置上也相邻,即利用存储位置上的相邻实现数据元素直接的逻辑相邻关系。
- 顺序表的类型定义
#define MAXSIZE 1024 /*顺序表可能的最大长度,假设为1024*/
typedef int elemtype /*elemtype可为任意类型,假设为int型*/
typedef struct sequlist
{
elemtype data[MAXSIZE]; /*定义顺序表为一维数组*/
int last; /*last为表中最后一个数据元素的下标位置*/
}SequenList; /*顺序表的结果类型为SequenList*/
其中,数据域 data是一个一维数组存放顺序表的数据元素,顺序表第1,2,…,n个元素依次存放在数组的第0,1,…,n-1下标元素位置上。MAXSIZE是数组data能容纳元素的最大个数,也称顺序表的容量。last是顺序表中最后一个元素的下标位置,亦代表顺序表的长度,当顺序表为空时,其last=-1,顺序表的长度则为0;非空时,长度为last+1。elemtype是顺序表数据元素的类型,视具体应用情况而定,如果顺序表是英文字母表,则elemtype就是字符型;如果顺序表是学生成绩表,则elemtype就是学生成绩的结构类型。
顺序表的基本运算
根据以上顺序表的结构类型定义,可以讨论在该存储结构上其基本运算的实现方法,即实现算法,同时对算法进行初步分析。
1、顺序表的初始化
顺序表的初始化就是构造一个空表。例如,将L设为顺序表指针变量,首先申请动态分配内存空间,如果申请分配内存成功,则将L的 last成员变量置为-1(因为此时表中还没有数据元素),然后返回申请的内存空间地址即顺序表的首地址;如果申请分配内存空间失败,则返回空指针。
SequenList *Init_SequenList()
{ SequenList *L; /*定义顺序表指针变量*/
L=(SequenList*)malloc(sizeof(SequenList));
/*申请分配内存空间*/
if (L!=NULL) /*申请分配内存空间成功*/
{ L->last=-1; /*设置顺序表的长度last 为一1,表示顺序表为空*/
}
return L; /*返回顺序表的首地址*/
}
设调用函数为主函数,其对初始化函数的调用如下。
void main()
{ SequenList*L;
L=Init_SequenList ();
if(L==NULL)
{ printf("申请顺序表内存空间失败,程序结束!\n");
return;
}
...
}
2、求顺序表的长度
顺序表结构类型中成员last指向顺序表中的最后一个元素的下标位置,所以顺序表的长度为L->last+1。
int SequenList_Length (SequenList*L)
{
return(L->last+1); /*返回顺序表的长度*/
}
3、插入
线性表的插入运算是指在表的第i(l≤i≤n+1)个位置上插入一个值为x的新结点,插入后使长度为n的线性表
(a1,a2,…,ai-1,ai,…,an)
变成长度为n+1的线性表
(a1,a2,…,ai-1,x,ai,…,an)
顺序表的结点在计算机中是连续存放的,若在第i个位置上插入一个新结点x,即在第i个结点之前插人一个新结点x,则必须将顺序表中下标为i-1,i,i+1,…,n-1上的结点依次向后移动成为下标是i,i+1,i+2,…,n的结点,空出第i个位置,然后将新结点x插入到该位置,如图2-4所示。当且仅当插人位置i=n+1时,无须移动结点,直接将新结点x插人到顺序表的末尾。新结点x插入后,线性表的长度变为n+1。
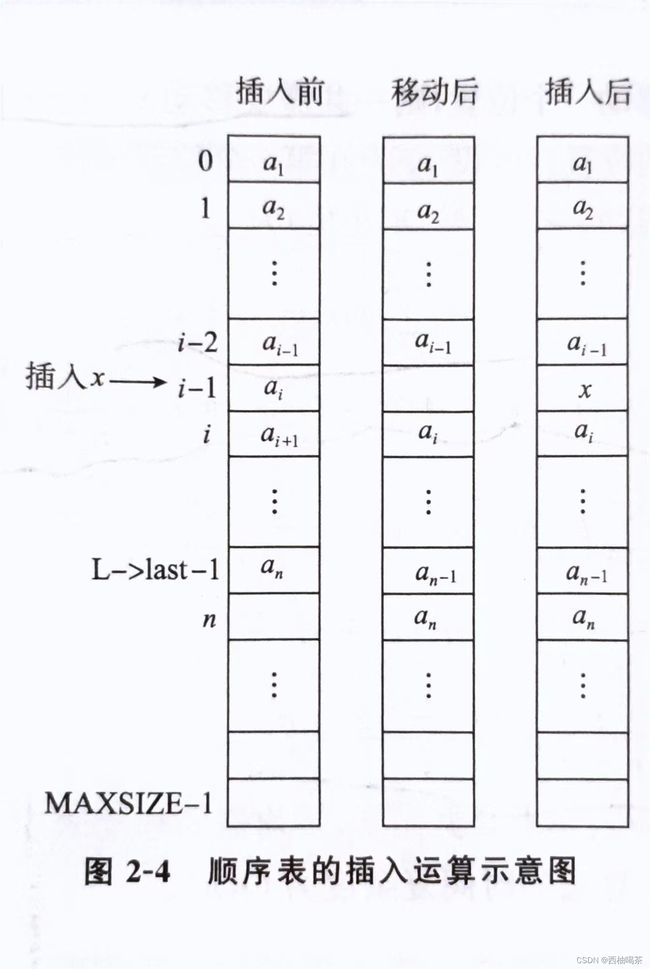
另外,插入一个数据元素必须确保顺序表的存储空间还有空闲,而且插人的位置必须合法,才能成功实现插入操作,否则插入操作就会失败。
顺序表的插入运算实现步骤如下。
- (1)检查顺序表的存储空间是否已满,若满则插入失败,返回值为0,否则进行第(2)步。
- (2)检测插入的位置
i是否合法,如果位置i<1或者i>L->last+2,则插入位置非法,插入操作失败,返回值为-1,否则进行第(3)步。 - (3)将第
i~n个结点之间的所有结点依次向后移动一个位置,空出第i个位置。 - (4)将新结点
x插入到第i个位置。 - (5)修改顺序表的长度,即使其加1,插人成功,函数返回值为1。
int Insert_SequenList(SequenList*L,elemtype x,int i)
/*在顺序表中指定的位置插入值为x的结点*/
/*L是SequenList类型的指针变量*/
/*x是待插入结点的数据元素值,i是在顺序表中的插入位置*/
{ intj;
if(L->last>=MAXSIZE-1) /*检查顺序表是否已满*/
{
return 0; /*顺序表满插入失败,函数返回0*/
}
if(i<1||i>L->last+2) /*插入位置有效性检查*/
{
return -1; /*位置非法,则插入失败,函数返回-1*/
}
for(j=L->last;j>=i-1;j--) /*在第i个位置插入新结点x*/
L->data[j+1]=L->data[j]; /*结点依次向后移动一个位置*/
L->data[i-1]=x; /*插入x到第i个位置*/
L->last=L->last+1; /*将顺序表长度加1*/
return 1; /*插入成功,函数返回1*/
}
(1)顺序表的数据区域只有MAXSIZE个存储单元,所以在顺序表中插入数据时必须先查表的空间是否已满,如果表已满就不能再进行插入操作,否则会产生溢出错误。
(2)对插入位置进行有效性检查,插入位置i的有效范围是1≤i≤n+1,其中n为原始表长。
(3)在插入过程中,要注意数据的移动方向。
4、删除
线性表的删除运算指将表的第i(l≤i≤n)个结点删除,使长度为n的线性表
(a1,a2,…,ai-1,ai,ai+1…,an)
变成长度为n-1的线性表
(a1,a2,…,ai-1,ai+1…,an)
如果要删除顺序表中第i个结点,就必须把表中第i+1个结点到第n个结点之间的所有结点依次向前移动一个位置,使顺序表的长度变为n-1,如图2-5所示。
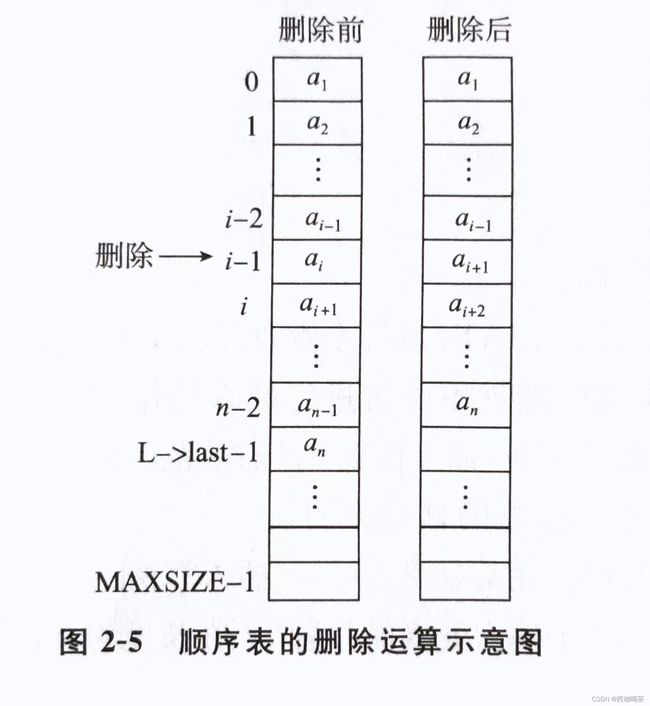
在顺序表中删除指定位置结点的步骤如下。
- (1)检查指定结点的删除位置是否有效,若删除位置无效,则删除失败,返回值为0,否则进行第(2)步。
- (2)将表中第
i+1~n个位置之间的所有结点依次向前移动一个位置。 - (3)将顺序表的长度减1,删除成功,函数返回1。
int Delete_SequenList(SequenList *L,int i)
/*删除第i个位置上的结点*/
{
int j;
if(i<1 || i>L->last+1) /*检查指定位置的有效性*/
{
return 0; /*位置非法删除失败,函数返回0*/
}
else
{
for(j=i;j<=L->last;j++)
L->data[j-1]=L->data[j]; /*结点前移*/
L->last--; /*表长减1*/
}
return 1; /*删除成功,函数返回1*/
}
(1)删除位置的有效性。删除第i个数据元素,i的有效范围为1≤i≤n,否则该元素不存在。
(2)当顺序表为空时,不能进行删除操作。由于顺序表为空时L->last=-1,条件 i<1||i>L->last+1亦包含了对该项的检查。
(3)删除ai之后,该数据已不存在,如果需要保留其值另做他用,则应先转存ai的值,然后再进行删除操作。
5、取数据元素
该运算是指取出顺序表中指定位置上的数据元素。因为顺序表中数据元素在计算机中连数据结构续存放,只要指定的位置i有效,则返回表中指定位置上的数据;否则位置错误,返回0。设顺序表的长度为n,则指定位置i的有效范围为l≤i≤n。
elemtype GetData_SequenList(SequenList *L,int i) /*顺序表取结点算法*/
{
if(i<1||i>L->last+1) /*位置有效性检查*/
{
return 0; /*位置无效,函数返回0*/
}
else
return(L->data[i-1]); /*返回所需结点的值*/
}
6、查找
线性表的查找运算是指在长度为n的线性表中查找与关键字key相等的数据元素。若查找成功,则返回key在顺序表中的位置;若查找失败,则返回0。在顺序表中实现本算法的步骤如下。
- (1)从顺序表的第一个数据元素ai开始,依次向后查找。
- (2)若第
i个数据元素与关键字key相等,则查找成功,函数返回key在表中的位置。 - (3)若查找失败,即表中不存在关键字
key值,则函数返回0。
int Search_SequenList(SequenList*L,elemtype key)
/*顺序表查找算法*/
{
int i;
for (i=0;i<=L->last;i++) /*表中元素依次与key进行比较*/
if(L->data[i]==key) /*找到与 key 相等的元素*/
{
return (i+1); /*返回其在顺序表中的位置*/
}
return 0; /*查找失败,返回0*/
7、遍历
所谓遍历就是从线性表的第一个数据元素开始,依次访问表中每一个元素并且仅访问一次。顺序表的遍历就是依次访问 a1~ an 的所有元素。访问时可以根据需要进行相关的操作,本算法在此仅输出该元素的值。
在顺序表中实现遍历算法的步骤如下。
- (1)判断顺序表是否为空,若为空,则返回0,遍历操作结束;否则进入第(2)步。
- (2)从顺序表的第一个数据元素开始输出所有元素,返回值为1,遍历操作结束。
int Print_SequenList(SequenList *L) /*顺序表遍历算法*/
{
int i;
if(L->last==-1) /*顺序表为空,返回值为0*/
{
return 0;
}
for(i=0;i<=L->last;i++)
{
printf("a[%2d]=%4d\t",i + 1,L->data[i]);
/*输出表中元素*/
if ((i+1)%5==0)
printf("\n"); /*控制每行输出的元素个数*/
}
return 1;
}
顺序表的应用
简单易懂,易上手,而且还是免费的!!!资源 ——>数据结构-顺序表
功能如下:
- 1、 顺序表的初始化
- 2、 求顺序表的长度
- 3、 在顺序表中插入结点
- 4、 在顺序表中删除结点
- 5、 在顺序表中取得结点
- 6、 在顺序表中查找
- 7、 顺序表遍历
- 8、 顺序表用后插法插入元素
- 9、 顺序表判空及判满
顺序表类型定义:
#define MAXSIZE 1024
typedef int elemtype;
typedef struct SequList //顺序表类型定义
{
elemtype data[MAXSIZE];
int last;
}SequenList;
所有用到的菜单:
/*所有被用到的函数先在下面声明*/
/*函数:主菜单*/
int Menu();
/*顺序表的初始化*/
SequenList * Init_SequenList();
/*求顺序表的长度*/
int SequenList_Length(SequenList *L);
/*在顺序表中插入结点*/
int Insert_SequenList(SequenList *L, elemtype x, int i);
/*在顺序表中删除结点*/
int Delete_SequenList(SequenList *L, int i);
/*在顺序表中取得结点*/
elemtype GetData_SequenList(SequenList *L, int i);
/*在顺序表中查找*/
int Search_SequentList(SequenList *L, elemtype key);
/*顺序表遍历*/
int Print_SequenList(SequenList *L);
/*顺序表用后插法插入元素*/
int InsertData_SequenList(SequenList *L, elemtype x);
顺序表的初始化:
/*顺序表的初始化*/
SequenList * Init_SequenList()
{
SequenList *L=NULL;
L=(SequenList*)malloc(sizeof(SequenList)); //配置顺序表空间
if(L!=NULL)
L->last=-1;
return L;
}
求顺序表的长度:
/*求顺序表的长度*/
int SequenList_Length(SequenList *L)
{
return(L->last+1);
}
在顺序表中插入结点:
/*在顺序表中插入结点*/
int Insert_SequenList(SequenList *L, elemtype x, int i)
{
int j;
if(L->last>=MAXSIZE-1)
return 0;
if(i<1 || i>L->last+2)
return -1;
for(j=L->last;j>=i-1;j--)
L->data[j+1]=L->data[j];
L->data[i-1]=x;
L->last=L->last+1;
return 1;
}
/*在顺序表中删除结点*/
int Delete_SequenList(SequenList *L, int i)
{
int j;
if(i<1 || i>L->last+1)
return 0;
else
{
for(j=i;j<=L->last;j++)
L->data[j-1]=L->data[j];
L->last--;
}
return 1;
}
/*在顺序表中取得结点*/
elemtype GetData_SequenList(SequenList *L, int i)
{
if(i<1 || i>L->last+1)
return 0;
else
return(L->data[i-1]);
}
运行截图:
……还有很多就不一一说了,需要的可以下载资源来看啊!
顺序表资源下载(免费哒!)
链接:数据结构-顺序表
【如果想要线性表的资源和文章可以点赞、关注+收藏哦!不定时更新哈哈~】