中药材鉴别-方法:聚类;PCA 主成分分析;线性判别式分析;判别式检验
基于线性判别式的中药材鉴别问题的数学模型
摘要
本文旨在讨论如何利用中药材的光谱特征鉴别药材的种类及产地,主要运用 系统聚类,PCA 主成分分析,线性判别,判别式运用等方法,使用了 MATLAB,Excel,SPSS 等工具,对中药材在近红外、中红外光谱数据进行分析,建立了最 优线性判别模型,用于鉴别中药材的种类及产地。
针对问题一, 首先通过对数据初步分析,发现部分不同编号药材在相同波 段光谱照射下的吸光度十分接近,进而使用差分一阶导数和差分二阶导数对光谱 图进行处理,经过对比发现,使用一阶导数比使用二阶导数具有更好的效果,不 仅消除了光谱的漂移,而且最大限度地体现了不同种类间光谱的差异,因此,本 题采用一阶导数对数据进行处理。经过观察,发现在 500cm-1-2000cm-1 与 2700cm
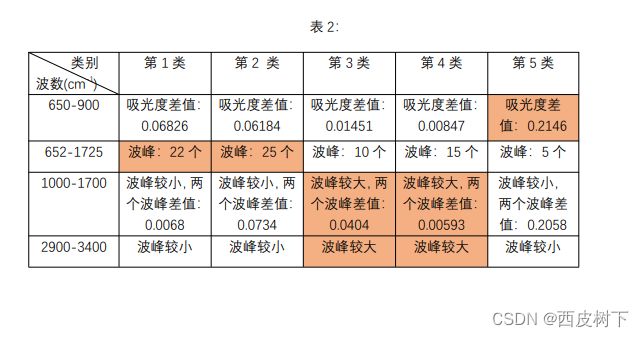
-1-3000cm-1的波段下,振幅相对明显,从而选取这两段数据进行标准正态 化处理。再将处理后的数据进行系统聚类,并计算欧氏距离得到谱系图,经检验 最终聚类为五类,再通过图像对比可见不同种类药材中红外光谱图的特征和差异 性,结果如表 2 所示。
针对问题二,根据附件二给出的数据,将每个产地 80%的数据作为训练集,建立线性判别分析模型,并将剩余数据作为测试集对模型进行检验,结果显示仅 1 个测试样本错判,模型准确率为 99.23%。接着对附件二中需要鉴别产地的中药 材进行鉴别。再用 PCA 主成分分析结合 SPSS 的判别式法检验线性判别分析模型 得出的结果,发现 PCA 主成分分析法与线性判别分析模型结果相同,因此我们将 线性判别分析模型所得结果分别作为最终结果如表8 所示,并使用MATLAB进行绘 图分析不同产地药材的特征和差异性。
针对问题三,首先将附件三中近红外数据和中红外数据合并,将 80%的数据 作为训练集,建立线性判别分析模型。再将剩余 20%数据作为测试集进行模型检 验,准确率达到 100%。接着对附件三中需要鉴别产地的中药材进行鉴别。为了 检验模型效果,依据问题二中主成分筛选,在通过运用 PCA 主成分分析法结合 SPSS 的判别式对近红光和中红外数据进行判别,判别式判别分析得出的结果与 线性判别分析模型的判别结果完成一致,最终鉴别药材的产地如表 17 所示。
针对问题四,根据附件四中数据,使用 MATLAB 编写代码建立类别判别模型。接着对产地建立线性判别分析模型,分别利用测试集进行模型检验,得到准确率 分别为 100%,79.17%。观察数据,对中药 A、B、C 分别建立线性判别分析模型,并使用各自测试集进行检验,得出准确率分别为 96.42%,100%,100%。进一步 分析数据后,建立各个类别的产地判别模型。为了检验模型效果,找出各个类型 产地的主成分特征值,建立特征值相关性矩阵,并运用 SPSS 的判别式检验各个 类型线性判别结果。最后建立线性判别分析模型,判别出需鉴别药材的类别与产 地,最终结果如表 30 所示。
关键词:聚类;PCA 主成分分析;线性判别式分析;判别式检验
一、 问题重述
1.1 问题背景
红外光谱是指分子能选择性吸收某些波长的红外线,而引起分子中振动能级 和转动能级的跃迁,通过检测红外线被吸收的情况可得到物质的红外吸收光谱。用红外光照射有机物分子时,分子中的化学键或官能团可发生振动吸收,不同的 化学键或官能团吸收频率不同,在红外光谱上将处于不同位置,从而可获得分子 中含有何种化学键或官能团的信息。
中药材有道地性的说法,它是指人们传统公认的且来源于特定产区的具有中 国特色的名优正品药材。中药材中含无机元素的化学成分、有机物等的差异性,在近红外、中红外光谱的照射下会表现出不同的光谱特征,可以利用这些特征来 鉴别中药材的种类及产地。
1.2 问题提出
(1)附件 1 中分别给出了多种中药材对中红外光谱不同光谱波数所对应的吸光 度数据,讨论分析从附件 1 中的数据能否体现中药材对中红外光谱不同光谱波数 所反映出相应的特征性和差异性,并鉴别中药材的种类。
(2)根据附件 2 中分别给出的多种中药材和不同产地对中红外光谱不同光谱波 数所对应的吸光度数据,讨论中药材对不同产地不同光谱波数的特征和差异性,并鉴别出中药材的产地,填充题目中所给出的表格。
(3)附件 3 中给出了分别给出的多种中药材和不同产地对中红外光谱不同光谱 波数所对应的吸光度数据和近红外光谱不同光谱波数所对应的吸光度数据,讨论 分析该种中药材的产地,并填充题目中所给出的表格。
(4)附件 4 中分别给出的多种中药材、不同产地、不同类型对中红外光谱不同 光谱波数所对应的吸光度数据,讨论分析中药材的类别和产地,并填充题目中所 给出的表格。
二、 问题分析
2.1 问题一的分析
问题一要求根据研究不同种类药材的特征和差异性,并鉴别药材的种类。首先,根据附件 1 中所给药材的中红外光谱数据,对原始光谱数据进行预处理,通 过不同的预处理方法(一阶导数、二阶导数)对原始光谱处理后发现,一阶导数 处理后的光谱图不仅消除了光谱的漂移而且最大限度地体现了不同产地对应光 谱段的差异。为减小实验误差,考虑到原始光谱数据基线漂移等影响,对原始光 谱数据进行标准正态变化预处理,消除了光谱的漂移和样本大小以及环境等因素 带来的谱线偏移,最大限度的滤除无用及干扰信号。将预处理数据导入 MATLAB 计算欧式距离并进行系统聚类和绘制谱系图。为了检验系统聚类效果将预处理数 据导入 SPSS,计算得出聚类系数,利用 Excel 软件绘制成聚类系数图,再使用 手肘法分析聚类系数得到分类数,并通过 MATLAB 工具分析不同药材的特征和差 异性。
2.2 问题二的分析
根据问题二要求,分析不同产地药材的特征和差异性,试鉴别药材的产地。首先将附件二的数据用 MATLAB 进行了线性判别分析,将原始数据按照比例分成 测试集和训练集进行模拟测试,线性判别分析在模拟测试上可以达到 99.23%的 正确率。为了更好检验线性判别分析,运用 PCA 主成分分析法并结合 SPSS 判别 式检验。在原始数据通过主成分分析,发现数据在主成分个数为 9 时贡献率最高,因此我们把所选取的主成分个数生成特征值相关性矩阵,并结合 SPSS 的判别式 检验,可以发现线性判别分析鉴别药材得出鉴别结果与线性判别分析结果一致。
2.3 问题三的分析
问题三要求根据附件 3 中数据,分析中药材的近红外和中红外数据,试鉴别 该种药材的产地。首先将附件三的数据用 MATLAB 进行了线性判别分析,依照问 题二的训练测试和主成分筛选,线性判别分析在测试集上可以达到 100%的正确 率。为了更好检验线性判别分析准确性,对近红光数据和中红光数据运用 PCA 主成分分析法,并结合 SPSS 的判别式检验,选择主成分个数分别是 5 个与 3 个,检验结果一致符合,所以我们认为线性判别分析可以鉴别某一种药材的产地。
2.4 问题四的分析
问题四要求根据附件 4 中数据,鉴别药材的类别及产地。首先利用 MATLAB 编写代码,将 A、B、C、三种中药 80%的数据作为训练集,建立类别判别模型。再将剩余的数据作为测试集进行测试,准确率 100%。再对数据进行线性判别,将数据进行测试和训练得出模拟测试准确率 79.17%。观察数据后发现中药 A、B 产地仅有 1-5 地,中药 B 有 1-16 地。为了提高测试准确率。于是对中药 A、B、C 分别建立线性判别分析模型。各个类型模拟测试准确率分别为 96.42%,100%,100%。最后分析数据后建立各个类别的产地判别模型。为了检验测试集准确效果,找出各个类型产地主成分特征值,建立特征值相关性矩阵,运用 SPSS 的判别式 检验各个类型,得出的结果与线性判别分析结果一致。
本论文具体解题思路如图:
三、 模型假设
1. 光谱图数据都在同一环境下测试
2. 药材不随时间的变化而改变对光波吸收
四、 符号说明
五、 模型建立与求解
5.1 问题一
5.1.1 数据预处理
在题目附件 1 中提供了 425 个药材在不同波段照射下的吸光度。将每个药材 测量的吸光度转换为光谱图,清楚直观的看出每个药材吸光度与波段之间的关系。因数据过多,为了方便制图,我们选择用 MATLAB 软件绘制(详细程序见附录):
图 1 原始数据近红外光谱折线图
观察图(1),发现数据过多而不便于分类,因此,基于图像是离散的数据这 一特性,建立定性测试方法,选择差分一阶导函数和差分二阶导函数两种方法对 数据进行处理(详细程序见附录):
图 2 差分一阶导数图
观察图 2、图 3 发现,在波数 500-4000cm-1的范围内,并非所有的谱图数据 都含有有效的信息,因此,我们希望能够对于种类分类最重要的的特征谱段,所 以选取出原函数图像上振幅较大的,波段为 500-2000cm-1与 2700-3000cm-1的数 据。
基于对数据的分析,可见光谱数据除了纯光谱之外还包含基线漂移、噪声等 信号,与此同时存在着因样本大小以及环境等因素带来的谱线偏移,所以在进行 特征分析前,利用 MATLAB 对选取出来的数据标准正态化(SNV:Standard Normal Variate)进行数据预处理(详细程序见附录),限于篇幅仅展示部分标准正太化 后的数据,如表 1 所示。
表 1 标准正态化数据图:
| No |
652 |
653 |
654 |
655 |
…… |
3999 |
| 1 |
0.094196 |
0.094057 |
0.094057 |
0.093992 |
…… |
0.009856 |
| 2 |
0.106043 |
0.105832 |
0.105832 |
0.105599 |
…… |
0.01742 |
| 3 |
0.27243 |
0.272049 |
0.272049 |
0.271811 |
…… |
0.005553 |
| 4 |
0.074814 |
0.074756 |
0.074756 |
0.074743 |
…… |
0.003266 |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
| 425 |
0.029449 |
0.029449 |
0.029468 |
0.029468 |
…… |

由图 6 可知,当 K<5 时,曲线急速下降;当 K>5 时,曲线趋于平稳,通过手 肘法我们认为拐点 5 为 K 的最佳值。结合图 5 可以看到当类间距离为 5.859 时,可以分为 5 类。把每一个分类得到的数据导入 MATLAB,得出中红外光谱曲线图,如图 7-11 所示。
观察图 7-11,可知在初始谱段 500-600cm-1范围内,第 5 类的光谱图初始吸 光数相对于其他类别的光谱图有明显差落,相对其他类别的光谱图波动性较明显,出现第一个高峰。而第 3 类、第 4 类的光谱图和第 1 类、第 2 类的光谱图在这个 谱段范围存在着较高的相似性。在谱段 750-2000cm-1范围内第 1 类、第 3 类、第 4 类的光谱图很容易看出有两个主峰,其中第 3 类的光谱图的第二主峰明显低于 第一主峰。第 5 类的光谱图只有一个主峰,第 2 类的光谱图吸光度波动剧烈。在 谱段 3000-3500cm-1范围内第 3 类、第 4 类的光谱图有着较明显波动性,第 1 类、第 2 类的光谱图在这个谱段范围波动性较平稳。对比分析如表 2 所示。
5.2 问题二
5.2.1:线性判别模型建立
5.2.2:线性判别求解
根据以上模型,选取附件 2 中 80%的数据作为训练集进行训练,选取附件 2 中 20%的数据作为测试集。
使用训练集对模型进行训练,完成训练后,再使用测试集对模型进行检验,得到如下结果:
表 3 测试集检验表
| No |
543 |
563 |
568 |
570 |
572 |
588 |
… |
665 |
| OP |
1 |
1 |
1 |
1 |
1 |
1 |
… |
11 |
| 模型判断 |
1 |
1 |
1 |
1 |
1 |
1 |
… |
11 |
根据模型给出的判断与原数据进行对比,发现模型判断的准确率高达 99.24%。将题目中要求鉴别产地的药材数据导入模型,得到以下结果:
表 4 药材产地鉴别表
| No |
3 |
14 |
38 |
48 |
58 |
71 |
79 |
86 |
89 |
110 |
134 |
152 |
227 |
331 |
618 |
| OP |
6 |
1 |
4 |
7 |
10 |
6 |
9 |
11 |
3 |
4 |
9 |
2 |
5 |
8 |
3 |
5.2.3:模型检验
将附件 2 中的数据导入 MATLAB 进行 PCA 主成分分析,提取中红外光谱数据 的特征信息,得到相应主成分的贡献率。根据每个主成分的贡献率和累计贡献率,选取合适的主成分建立判别式模型。
表 5 贡献率信息表
| 主成分 |
Pc1 |
Pc2 |
Pc3 |
Pc4 |
Pc5 |
Pc6 |
Pc7 |
Pc8 |
Pc9 |
| 贡献率 |
80.7% |
9.14% |
5.06% |
2.24% |
0.86% |
0.55% |
0.46% |
0.29% |
0.07% |
| 主成分 |
Pc10 |
Pc11 |
Pc12 |
Pc13 |
Pc14 |
Pc15 |
Pc16 |
Pc17 |
Pc18 |
| 贡献率 |
0.06% |
0.05% |
0.04% |
0.03% |
0.02% |
0.02% |
0.01% |
0.01% |
0.01% |
由表 5 知前 4 个主成分累计贡献率为 97.15%,因此选取前四个主成分作为 后续分析的主成分数.
将主成分分析后的结果分别导入 SPSS 进行判别式运算,所得结果如下表格 所示:
表 6 判别式判别表
| NO |
1 |
2 |
3 |
4 |
5 |
6 |
… |
673 |
| 实际产地 |
11 |
1 |
3 |
6 |
7 |
8 |
… |
1 |
| 模型判别 |
11 |
1 |
6 |
6 |
7 |
8 |
… |
1 |
| 正确率 |
91.05% |
由表 6 判别结果准确率为 91.06%,判别效果在误差范围内。对题目中要求鉴 别产地药材进行判别得到以下结果:
表 7 药材产地判别表
| No |
3 |
14 |
38 |
48 |
58 |
71 |
79 |
86 |
89 |
110 |
134 |
152 |
227 |
331 |
618 |
| OP |
6 |
1 |
4 |
7 |
10 |
6 |
9 |
11 |
3 |
4 |
9 |
2 |
5 |
8 |
3 |
将表 4 与表 7 进行对比,发现结果重合率为 100%。则表 4(表 7)即为判别 最终结果。
将原数据中空缺的 OP 补全,将相同 OP 的药材分为同一类,绘制红外光谱图:
图 13 红外光谱均值折线图
根据图 13 可以直观地看出光谱图大致上都具有一定的相似性,我们初步分 析得出了三个峰位从而进行对峰位的讨论:
第一主峰:
在波数为 1000-1100cm-1范围内一个波峰,产地为 2 的药材有吸光度最高的 波峰,产地为 4 的药材有吸光度最低的波峰,其余产地为 8、9、6、7、10、5、3、1、11 的药材在此波数内吸光度波峰的高度从高到低依次排列,且位于始波 峰都要低于位于尾波峰;产地为 1,2,3,8 ,11 的药材,在始波峰到尾波峰范围内 振幅趋势较大;产地为 4,5,6,7 ,9,10 的药材,在始波峰到尾波峰范围内振幅趋 势较平稳
第二主峰:
在波数为大概 1313cm-1的范围内一个波峰,产地为 9 的药材有吸光度最高的 波峰,产地为 3 的药材有吸光度最低的波峰其余产地为 5、10、6、2、7、8、4、11、1 的药材在此波数内吸光度波峰的高度从高到低依次,所有药材在这个波数 范围内具有相似性
第三主峰:
在波数为 3400-3500cm-1范围内有一个波峰,产地为 8 的药材有吸光度最高 的波峰,产地为 4 的药材有吸光度最低的波峰,其余产地为 2、6、5、3、1、9、11、10 的药材在此波数内吸光度波峰的高度从高到低依次排列,且位于始波峰 都要高于位于尾波峰;产地为 1,2,3,8,10,11 的药材,在始波峰到尾波峰范围内 都具有下滑趋势,其余均为平滑趋势。
分析各个产地不同主峰的峰位表现,如下表所示: 表 8

5.3 问题三
5.3.2 模型求解
考虑到附件 3 的样本数据较少,决定建立中红外和近红外线性分析判别模型,从两个方面来综合鉴别。将中红外光谱数据分为 17 类,分别是 1-17,并把这 17 个产地在原始数据 80%的数据作为训练集,20%的数据为测试集建立类型判别模 型。对近红外光谱数据进行同样操作。所得结果绘制图表:
表 9 近红外测试集检验表
| NO |
172 |
176 |
177 |
182 |
186 |
192 |
… |
255 |
| 实际产地 |
3 |
13 |
3 |
3 |
13 |
5 |
… |
6 |
| 判别 |
3 |
13 |
3 |
3 |
13 |
5 |
… |
6 |
| 正确率 |
98.08% |
表 10 中红外测试集检验表
| NO |
172 |
176 |
177 |
182 |
186 |
192 |
… |
255 |
| 实际产地 |
3 |
13 |
3 |
3 |
13 |
5 |
… |
6 |
| 判别 |
3 |
13 |
3 |
3 |
13 |
5 |
… |
6 |
| 正确率 |
98.08% |
根据表 9-10 可以看出类型判别模型在训练集的训练下,测试集数据判别为 均为准确率为 98.08%%。将题目中要求鉴别产地的药材数据导入模型,得到以下 结果:
表 11 药材产地判别表
| No |
4 |
15 |
22 |
30 |
34 |
45 |
74 |
114 |
170 |
209 |
| 近红外 |
17 |
11 |
1 |
2 |
16 |
3 |
4 |
10 |
9 |
14 |
| 中红外 |
17 |
11 |
1 |
2 |
16 |
3 |
4 |
10 |
9 |
14 |
5.3.2 模型检验
将附件 3 中的近红光与中红光数据导入 MATLAB 进行 PCA 主成分分析,提取 中红外光谱数据的特征信息,得到相应主成分的贡献率。根据每个主成分的贡献 率和累计贡献率,选取合适的主成分建立判别式模型:
特征信息图分别为:
表 12 近红光主成分贡献表
| 主成分 |
Pc1 |
Pc2 |
Pc3 |
Pc4 |
Pc5 |
Pc6 |
Pc7 |
Pc8 |
| 贡献率 |
69.2% |
24.4% |
4.16% |
0.94% |
0.38% |
0.32% |
0.21% |
0.15% |
表 13 中红光主成分贡献表
| 主成分 |
Pc1 |
Pc2 |
Pc3 |
Pc4 |
Pc5 |
Pc6 |
Pc7 |
Pc8 |
| 贡献率 |
89.9% |
5.9% |
2.27% |
0.78% |
0.29% |
0.21% |
0.14% |
0.10% |
由表 12 和表 13 知,近红光与中红光前 8 个主成分累计贡献率分布为 99.86%,99.59%,因此选取前四个主成分为特征值作为后续分析的主成分数。
将选取的主成分建立特征值相关性矩阵分别结合 SPSS 进行判别式运算,所 得结果如下表格所示:
表 14 近红光判别表
| NO |
1 |
2 |
3 |
4 |
5 |
6 |
… |
673 |
| OP |
11 |
1 |
3 |
6 |
7 |
8 |
… |
1 |
| 预测 |
11 |
1 |
6 |
6 |
7 |
8 |
… |
1 |
| 正确率 |
97.14% |
表 15 中红光判别表
| NO |
1 |
2 |
3 |
4 |
5 |
6 |
… |
673 |
| OP |
11 |
1 |
3 |
6 |
7 |
8 |
… |
1 |
| 预测 |
11 |
1 |
6 |
6 |
7 |
8 |
… |
1 |
| 正确率 |
89.79% |
由表 14-15 可知,判别结果准确率分别为 97.14%, 89.79%。判别效果在误 差范围内。将题目中要求鉴别产地的药材数据导入模型,得到结果并于线性判别 和判别式分析模型得到的结果绘制在一起:
表 16 近红外与中红光判定结果
| NO |
4 |
15 |
22 |
30 |
34 |
45 |
74 |
114 |
170 |
209 |
| 近红外 |
17 |
11 |
1 |
2 |
16 |
3 |
4 |
10 |
9 |
14 |
| 中红外 |
17 |
11 |
1 |
2 |
16 |
3 |
4 |
10 |
9 |
14 |
| 近红外 |
17 |
11 |
1 |
2 |
16 |
3 |
4 |
10 |
9 |
14 |
| 中红外 |
17 |
6 |
1 |
2 |
16 |
3 |
4 |
10 |
9 |
14 |
根据题目所要鉴别的数据,分别运用近红外和中红外数据,运用线性判别分 析模型得到的结果与判别式得到的结果进行对比,从表 16 中可见,编号为 15 号的药材分类出现差异,结合所有的判别结果进行筛选,其他模型判别均为产地 11,考虑中红外判别式模型正确率相对较低,最终确认编号 15 号为产地 11。到 因此对题目中要求鉴别产地药材进行判别分析得到以下结果:
表 17 药材与产地鉴别表
| No |
4 |
15 |
22 |
30 |
34 |
45 |
74 |
114 |
170 |
209 |
| OP |
17 |
11 |
1 |
2 |
16 |
3 |
4 |
10 |
9 |
14 |
5.4 问题四
5.4.1 模型求解:
根据附件 4 的数据分为三类,分别是 A、B、C,并把这三种中药对应原始数 据 80%的数据作为训练集,20%的数据为测试集,建立类型判别模型所得结果绘 制图表:
表 18 类别测试集检验表
| No |
298 |
306 |
314 |
317 |
318 |
319 |
… |
398 |
| 实际类别 |
C |
C |
B |
B |
C |
B |
… |
B |
| 判别类别 |
C |
C |
B |
B |
C |
B |
… |
B |
| 准确率 |
100% |
根据表 18 可以看出类型判别模型在训练集的训练下,测试集数据判别为准 确率为 100%.用判别类别结果填充附件 4 类别为空值的数据,因此对题目中要求 鉴别类别药材得到结果如下表所示。
表 19 药材类别表
| No |
94 |
109 |
140 |
278 |
308 |
330 |
347 |
| Class |
A |
A |
A |
C |
C |
C |
B |
同理,以产地 1-16 原始数据的 80%为训练集建立产地判别模型,20%的数据 为测试集建立类型判别模型所得结果绘制图表:
表 20 产地测试集检验表
| No |
247 |
293 |
294 |
295 |
299 |
307 |
… |
399 |
| 实际类别 |
9 |
12 |
2 |
14 |
6 |
2 |
… |
13 |
| 判别类别 |
9 |
12 |
2 |
14 |
6 |
1 |
… |
13 |
| 准确率 |
79.17% |
根据表 20 可知模型正确率并不是很理想,因此在类型判别模型基础上。分 别把不同类型 A、B、C 分成三类,以每一类原有数据 80%的数据作为训练集,20% 的数据为测试集进行,分别得出每一类的测试情况并把数据绘制成图表:
表 21 A 类产地测试集检验表
| No |
53 |
67 |
79 |
156 |
197 |
203 |
… |
392 |
| 实际产地 |
5 |
1 |
5 |
4 |
4 |
4 |
… |
4 |
| 判别产地 |
5 |
1 |
5 |
4 |
2 |
4 |
… |
4 |
| 准确率 |
96.42% |
表 22 B 类产地测试集检验表
| No |
18 |
73 |
82 |
128 |
129 |
144 |
… |
399 |
| 实际产地 |
7 |
14 |
13 |
6 |
4 |
7 |
… |
13 |
| 判别产地 |
7 |
14 |
13 |
6 |
4 |
7 |
… |
13 |
| 准确率 |
100% |
表 23 C 类产地测试集检验表
| No |
36 |
50 |
101 |
125 |
137 |
154 |
… |
376 |
| 实际产地 |
3 |
2 |
3 |
3 |
2 |
2 |
… |
4 |
| 判别产地 |
3 |
2 |
3 |
3 |
2 |
2 |
… |
4 |
| 准确率 |
100% |
根据表 21-23,可以得出同一个类型鉴别不同产地的药材准确性分别为 96.42%,100%,100%。最后将题目中要求鉴别产地的药材数据导入模型,得到以 下结果:
表 24 产地类别判别表
| No |
94 |
109 |
140 |
278 |
308 |
330 |
347 |
| Class |
A |
A |
A |
C |
C |
C |
B |
| OP |
5 |
3 |
1 |
1 |
3 |
4 |
12 |
5.4.3 模型检验:
通过 PCA 主成分分析得出特征值,所得结果如下表格所示:
表 25 特征信息表
| 主成分 |
PC1 |
PC2 |
PC3 |
PC4 |
PC5 |
PC6 |
PC7 |
| A |
90.23% |
7.83% |
1.24% |
0.55% |
0.08% |
0.03% |
0.01% |
| B |
66.7% |
25.7% |
6.88% |
0.29% |
0.17% |
0.11% |
0.06% |
| C |
90.22% |
7.83% |
1.24% |
0.6% |
0.08% |
0.03% |
0.01% |
根据表 25,可知类型 A,B,C 前 8 个主成分累计贡献率分别为 99.85%,99.58%,99.85%因此选取前八个主成分为特征值作为后续分析的主成分数.将选取的主成 分建立特征值相关性矩阵分别结合 SPSS 进行判别式运算。
我们将类性判别得到的数据,进行数据填补,并使用判别式对每一个类型的 数据进行判别,分别得到不同类别的数据,并把数据整理分析:
表 26 A 类测试表
| No |
13 |
16 |
19 |
23 |
24 |
28 |
… |
397 |
| 实际产地 |
1 |
4 |
3 |
5 |
3 |
3 |
… |
3 |
| 判别产地 |
1 |
4 |
3 |
5 |
3 |
3 |
… |
3 |
| 准确率 |
86.15% |
表 27 B 类测试表
| No |
1 |
3 |
6 |
7 |
11 |
15 |
… |
399 |
| 实际产地 |
16 |
10 |
13 |
9 |
14 |
9 |
… |
13 |
| 判别产地 |
16 |
10 |
13 |
9 |
14 |
9 |
… |
13 |
| 准确率 |
88% |
表 28 C 类测试表
| No |
5 |
8 |
17 |
20 |
22 |
26 |
… |
391 |
| 实际产地 |
3 |
3 |
4 |
2 |
4 |
2 |
… |
2 |
| 判别产地 |
3 |
3 |
4 |
2 |
4 |
2 |
… |
2 |
| 准确率 |
100% |
由表 26-28 可知判别结果准确率分别为 86.15%,88%, 100%。判别效果在误 差范围内。根据题目所要鉴别的数据我们运用线性判别分析模型得到的结果与判 别式得到的结果进行对比,发现结果重合率分别为 80%,84.61%,100%。 将三种判别模型结果汇聚,如下表所示。
表 29 产地鉴别表
| No |
94 |
109 |
140 |
278 |
308 |
330 |
347 |
| Class |
A |
A |
A |
C |
C |
C |
B |
| OP |
5 |
3 |
1 |
1 |
3 |
3 |
11 |
| OP |
5 |
3 |
1 |
1 |
3 |
4 |
12 |
| OP |
5 |
3 |
1 |
1 |
3 |
4 |
11 |
OP 分别为以原始数据训练出的产地判别模型判别的产地、将数据分类后分 别训练的产地判别模型判别的产地和判别式判别的产地。347 号和 330 号出现差 异,取重复次数较多的产地作为最终结果,因此对题目中要求鉴别产地药材进行 判别分析得到以下结果:
表 30 药材与产地鉴别表
| No |
94 |
109 |
140 |
278 |
308 |
330 |
347 |
| Class |
A |
A |
A |
C |
C |
C |
B |
| OP |
5 |
3 |
1 |
1 |
3 |
4 |
11 |
六、模型评价与改进
6.1 优点
1. 对问题的求解采用两种预测模型来评估分类的性能
2. PCA 主成分模型建立对数据进行降维,充分体现主成分的指标
3. 对问题的求解有合理的
6.2 缺点
1.如果时间允许,可以使用多种方法进行模型检验。
2.没有考虑原数据重复值对 PCA 主成分分析的影响,可能存在一些实验误差。
6.3 改进
1.应尝试多种判别进行比较,选择判别效果最好的一种。
七、参考文献
[1]刘沭华,张学工,孙素琴.中药材产地的近红外光谱自动鉴别和特征谱段选择 [J].科学通报,2005(04):393-398.
[1]岑忠用,雷顺新,雷蕾,严军,张晖英.近红外光谱法鉴别 6 种根茎类中药材[J]. 华中农业大学学报,2021,40(03):271-277.
[1]黄得栋,何微微,马晓辉,林丽,朱田田,晋玲.近红外光谱法鉴别不同产地的南 五味子[J].中兽医医药杂志,2018,37(02):47-50.
[1]孔德明,董瑞,崔耀耀,王书涛,史慧超.基于三维荧光光谱结合二维线性判别 分析的油类识别方法的研究[J].光谱学与光谱分析,2021,41(08):2505-2510. [1]刘辉,李静,曾昭发,王天琪.基于贝叶斯理论面波频散曲线随机反演[J].物探 与化探,2021,45(04):951-960.
八、附录清单
代码和数据