2013年蓝桥杯省赛C++B组真题与题解

1 高斯日记

题目：

大数学家高斯有个好习惯：无论如何都要记日记。

他的日记有个与众不同的地方，他从不注明年月日，而是用一个整数代替，比如：4210

后来人们知道，那个整数就是日期，它表示那一天是高斯出生后的第几天。这或许也是个好习惯，它时时刻刻提醒着主人：日子又过去一天，还有多少时光可以用于浪费呢？

高斯出生于：1777年4月30日。
在高斯发现的一个重要定理的日记上标注着：5343，因此可算出那天是：1791年12月15日。

高斯获得博士学位的那天日记上标着：8113

请你算出高斯获得博士学位的年月日。

提交答案的格式是：yyyy-mm-dd, 例如：1980-03-21

请严格按照格式，通过浏览器提交答案。 注意：只提交这个日期，不要写其它附加内容，比如：说明性的文字。

题解：
已知5343是1791年12月15日，求8113对应日期，本题需要计算的数字较小，因此可以用Excel直接求解。如下图中，依次从1791年开始加每年的数字，A栏是年份，B栏是该年天数，C栏是从5343开始依次加上该年天数后的数字，如C2栏即为5343加上1791年剩余的16天后的数字，C3栏即为加完1792年整年366天后的数字，E栏为当年年份除以4后得到的数字，若为整数且该年年数不是100的整数则该年为闰年，按366天算。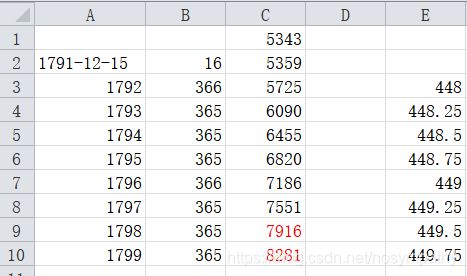

发现8113在1798年和1799年之间，可得8113减去7916为197，依次减去每月天数，如下，

可知减完6月份时还剩16天，可得出所求日期为1799-07-16

2 马虎的算式

题目：

小明是个急性子，上小学的时候经常把老师写在黑板上的题目抄错了。

有一次，老师出的题目是：36 x 495 = ?

他却给抄成了：396 x 45 = ?

但结果却很戏剧性，他的答案竟然是对的！！

因为 36 * 495 = 396 * 45 = 17820

类似这样的巧合情况可能还有很多，比如：27 * 594 = 297 * 54

假设 a b c d e 代表1~9不同的5个数字（注意是各不相同的数字，且不含0）

能满足形如： ab * cde = adb * ce 这样的算式一共有多少种呢？

请你利用计算机的优势寻找所有的可能，并回答不同算式的种类数。

满足乘法交换律的算式计为不同的种类，所以答案肯定是个偶数。

题解：
找出满足ab * cde = adb * ce算式的答案个数，a b c d e是代表1~9不同的5个数字。只要满足该算式即计为不同种类，所以不存在重合问题，一共只有5种数字，可以直接暴力计算。只需要注意判断每个数字都不相同和判断算式的满足。代码如下：

3 第39级台阶

题目：

小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!

站在台阶前，他突然又想着一个问题：

如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？

请你利用计算机的优势，帮助小明寻找答案。

要求提交的是一个整数。 注意：不要提交解答过程，或其它的辅助说明文字。

题解：
一共39级台阶，每一步上1级或2级台阶，也就是每上一次台阶，选择上1级或2级，剩下的台阶再选择上1级或2级，逐步递推，直到走完39级台阶，中间加上步数这个参数，最后判断步数是不是偶数，是的话就算进答案个数里。代码如下：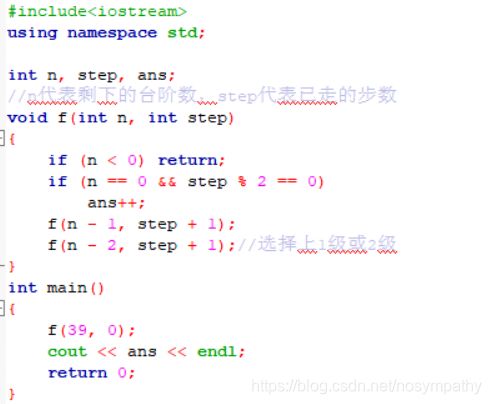

4 黄金连分数

题目：

黄金分割数0.61803… 是个无理数，这个常数十分重要，在许多工程问题中会出现。有时需要把这个数字求得很精确。

对于某些精密工程，常数的精度很重要。也许你听说过哈勃太空望远镜，它首次升空后就发现了一处人工加工错误，对那样一个庞然大物，其实只是镜面加工时有比头发丝还细许多倍的一处错误而已，却使它成了“近视眼”!!

言归正传，我们如何求得黄金分割数的尽可能精确的值呢？有许多方法。

比较简单的一种是用连分数：

              1
黄金数 = ---------------------
                    1
         1 + -----------------
                      1
             1 + -------------
                        1
                 1 + ---------
                      1 + ...

这个连分数计算的“层数”越多，它的值越接近黄金分割数。

请你利用这一特性，求出黄金分割数的足够精确值，要求四舍五入到小数点后100位。

小数点后3位的值为：0.618 小数点后4位的值为：0.6180 小数点后5位的值为：0.61803
小数点后7位的值为：0.6180340 （注意尾部的0，不能忽略）

你的任务是：写出精确到小数点后100位精度的黄金分割值。

注意：尾数的四舍五入！ 尾数是0也要保留！

显然答案是一个小数，其小数点后有100位数字，请通过浏览器直接提交该数字。 注意：不要提交解答过程，或其它辅助说明类的内容。

题解：
求黄金分割数，由连分数的层级可联想到递归，但单纯的递归无法求精确到小数点后100位的黄金分割数，若用连分数求，按层级依次为1，1/2，2/3，3/5，5/8,…….由此可想到斐波那契数列，又称黄金分割数列，为1、1、2、3、5、8、13、21、34……此数列从第3项开始，每一项都等于前两项之和，而此题最终要求的小数点后100位精度即为斐波那契数列中某两项相除得到的值，因此该题转化为求斐波那契数列的某两项的商精确到小数点后100位。因为涉及到的数字过大所以不能用已经规定的数据类型定义，我选择用C++中的vector类型储存需要得到的两项数字和最终答案即小数点后100位数字。前面的定义如下：

至于n为什么是300，后面会有解释。
首先是主函数，因为已知前两项是1，所以直接先push进A和B，接下来就是不断的求和，清空，和替换A和B的数据，保证A始终小于B，这里使用的高精度加法模板add()之前发过解析，就不过多解释。

这样就求出了斐波那契数列中我们需要的那两项数字了,接下来就是求A和B相除的结果，这里需要将除法转换成减法，其原理如下：比如要求1/3，将1后面添个0，得到10，用10去减3，一共可以减3次，这个减的次数就是小数点后的第一位，减完余1，再在这个1后面添个0，继续去减3，这次减的次数就是小数点后的第二位了，以此类推，想要得到小数点后100位至少得完成100次这样的操作，主函数实现如下：（高精度减法sub函数和判断A和B大小cmp的解析同上，若需详细解析，可看基础算法-高精度的加、减、乘、除运算-C++实现）

最后按照小数的格式输出，这里要注意，虽然只需要求小数点后100位，但不能只把n设置为101，还要加大n的值多试几次，直到求出的小数点后100位的值稳定了才是最终答案，且要求到101位再四舍五入。
比如，n=101时，小数点后101位：0.61803398874989484820458683436563811772030898118204323171968168093976058120430545788325825154507567808
n=200时，小数点后101位：0.61803398874989484820458683436563811772030917980576286213544862270526046281890244970803605876859146255
n=300时，小数点后101位：0.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748
n=400时，小数点后101位：0.61803398874989484820458683436563811772030917980576286213544862270526046281890244970720720418939113748
可以看到直到n=300的时候小数点后100位数字才稳定，此时得到的才是正确答案，再四舍五入下，就得到最终答案了，全部代码如下：

#include
#include
#include
using namespace std;

vector<int> A, B, C, ans;
int n = 300;

bool cmp(vector<int> &A, vector<int> &B)//比较A与B大小
{
    if (A.size() != B.size()) return A.size() > B.size();
    for (int i = A.size() - 1; i >= 0; i --)
        if (A[i] != B[i]) return A[i] > B[i];
    return true;
}

vector<int> add(vector<int> &A, vector<int> &B)//高精度加法
{
    if (A.size() < B.size()) return add(B, A);
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++)
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(1);
    return C;
}

vector<int> sub(vector<int> &A, vector<int> &B)//高精度减法
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++)
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    A.push_back(1);
    B.push_back(1);
    for (int i = 1; i <= n; i ++)
    {
        C = add(A, B);
        A.clear();
        for (int i = 0; i < B.size(); i ++) A.push_back(B[i]);
        B.clear();
        for (int i = 0; i < C.size(); i ++) B.push_back(C[i]);
        C.clear();
    }//求出斐波那契数列中需要的两项A和B

    reverse(A.begin(), A.end());
    A.push_back(0);
    reverse(A.begin(), A.end());
    //此时A是倒着存储的，需要转过来才能在A后面添0
    while (ans.size() < n)//ans存储小数点后每一位数
    {
        int t = 0;//t存储做减法的次数
        while(cmp(A, B))//若A大于B则进行A减B操作
        {
            A = sub(A, B);
            t ++;
        }
        reverse(A.begin(), A.end());
        A.push_back(0);
        reverse(A.begin(), A.end());//减到A小于B继续添0

        ans.push_back(t);//将减的次数存入答案
    }
    cout << "0.";
    for (int i = 0; i < 99; i ++) cout << ans[i];
    if (ans[100] >= 5) cout << ans[99] + 1 << endl;
    else cout << ans[99] << endl;
    return 0;
}

5 前缀判断

题目：

如下的代码判断 needle_start指向的串是否为haystack_start指向的串的前缀，如不是，则返回NULL。

比如：“abcd1234” 就包含了 “abc” 为前缀

char* prefix(char* haystack_start, char* needle_start)
{
	char* haystack = haystack_start;
	char* needle = needle_start;

	
while(*haystack && *needle){
		if(______________________________) return NULL;  //填空位置
	}
	
if(*needle) return NULL;
	
return haystack_start;
}

题解：
判断 needle_start指向的串是否为haystack_start指向的串的前缀，先将程序编译，没有错误之后读程序，函数中定义了haystack和needle字符指针指向haystack_start和needle_start指向字符串的第一个字符：char* haystack = haystack_start; char* needle = needle_start; 同时从头遍历并比较两个字符串的每个字符 while(*haystack && *needle)，需要对haystack和needle指向的字符进行是否相等的判断，若不相等则返回空，同时要将指针向后移动，该操作在需要填的空中实现，即*(haystack++)!=*(needle++),遍历停止后若子串没有遍历完则也说明不是字符串前缀，返回空if(*needle) return NULL; 若前面的判断都通过了没有返回空，则说明判断成功，则返回母字符串。填完后在程序中添加主函数测试函数功能是否能实现。

6 三部排序

题目：

一般的排序有许多经典算法，如快速排序、希尔排序等。

但实际应用时，经常会或多或少有一些特殊的要求。我们没必要套用那些经典算法，可以根据实际情况建立更好的解法。

比如，对一个整型数组中的数字进行分类排序：

使得负数都靠左端，正数都靠右端，0在中部。注意问题的特点是：负数区域和正数区域内并不要求有序。可以利用这个特点通过1次线性扫描就结束战斗!!

以下的程序实现了该目标。

其中x指向待排序的整型数组，len是数组的长度。

void sort3p(int* x, int len)
{
	int p = 0;
	int left = 0;
	int right = len-1;
	
while(p<=right){
		if(x[p]<0){
			int t = x[left];
			x[left] = x[p];
			x[p] = t;
			left++;
			p++;
		}
		else if(x[p]>0){
			int t = x[right];
			x[right] = x[p];
			x[p] = t;
			right--;			
		}
		else{
			__________________________;  //填空位置
		}
	}
	
}

如果给定数组：
25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0
则排序后为：
-3,-2,-16,-5,0,0,0,21,19,33,25,16,18,25

题解：
对整形数组分类排序，使得负数都靠左端，正数都靠右端，0在中部。注意负数区域和正数区域内并不要求有序。函数中p为指向数组内数字的指针，left指针从前向后移动，right指针从后向前移动，用while(p<=right)判断数组是否遍历完，依次遍历数组中的数，若x[p]小于0，则将其与数组左边的数交换 int t = x[left]; x[left] = x[p]; x[p] = t;并将p和left指针都右移，若x[p]大于0，则将其与数组右边的数交换 int t = x[right]; x[right] = x[p]; x[p] = t;并将right指针左移。剩下的填空处即为x[p]等于0的情况，不需进行处理，只需将p指针右移，即p++

7 错误票据

题目：

某涉密单位下发了某种票据，并要在年终全部收回。

每张票据有唯一的ID号。全年所有票据的ID号是连续的，但ID的开始数码是随机选定的。

因为工作人员疏忽，在录入ID号的时候发生了一处错误，造成了某个ID断号，另外一个ID重号。

你的任务是通过编程，找出断号的ID和重号的ID。

假设断号不可能发生在最大和最小号。

要求程序首先输入一个整数N(N<100)表示后面数据行数。 接着读入N行数据。
每行数据长度不等，是用空格分开的若干个（不大于100个）正整数（不大于100000） 每个整数代表一个ID号。

要求程序输出1行，含两个整数m n，用空格分隔。 其中，m表示断号ID，n表示重号ID

例如：
用户输入：
2 5 6 8 11 9 10 12 9

则程序输出：
7 9

再例如：
用户输入：
6 164 178 108 109 180 155 141 159 104 182 179 118 137 184
115 124 125 129 168 196 172 189 127 107 112 192 103 131 133 169 158
128 102 110 148 139 157 140 195 197 185 152 135 106 123 173 122 136
174 191 145 116 151 143 175 120 161 134 162 190 149 138 142 146 199
126 165 156 153 193 144 166 170 121 171 132 101 194 187 188 113 130
176 154 177 120 117 150 114 183 186 181 100 163 160 167 147 198 111
119

则程序输出：
105 120

题解：
要找出断号和重号的ID，根据题目要求，读入N行数据，每行的ID数量未知，只能按行读入，需要用到getline读取，并用字符串输入流stringstream依次读取以空格为分隔符的数字字符，再将数字字符转换为数字存入数组，由于ID是按顺序排的，所以可以直接对数组进行排序，按顺序查找断号和重号。代码及注释如下：

#include
#include
#include
#include
using namespace std;
const int N = 10005;
//行数100以内，每行ID个数100以内，数据范围10000 
int id[N];
int line, m, n, index;
//m存断号ID，n存重号ID，index指示ID数量 
int main()
{
    scanf ("%d", &line);
    getchar();//由于后面是 getline需要把换行符读走 
    for (int i = 0; i < line; i ++)
    {
        string s, tmp;
        getline(cin, s); 
        istringstream iss(s);//iss获取s中的string对象 
        while (getline(iss, tmp, ' '))//以空格为分隔符依次读入每个ID 
        {
            stringstream ss;//创建stringstream对象 
            ss << tmp;//将tmp中的数字字符读入到ss里 
            ss >> id[index++];//将ss里的数字读入到数组里 
        }
    }
    sort (id, id + index);//对ID排序 
    for (int i = 1; i < index; i ++)
    {
        if (id[i] == id[i - 1] + 2) m = id[i] - 1;
        if (id[i] == id[i - 1]) n = id[i];
    }
    cout << m << ' ' << n << endl;
    return 0;
}

8 翻硬币

题目：

小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用 * 表示正面，用 o 表示反面（是小写字母，不是零）。
比如，可能情形是：oo*oooo
如果同时翻转左边的两个硬币，则变为：oooo***oooo
现在小明的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币,那么对特定的局面，最少要翻动多少次呢？
我们约定：把翻动相邻的两个硬币叫做一步操作，那么要求：
程序输入： 两行等长的字符串，分别表示初始状态和要达到的目标状态。每行的长度<1000 程序输出： 一个整数，表示最小操作步数

例如：
用户输入：

**********
 o****o****

程序应该输出：
5
再例如：
用户输入：

*o**o***o***  
*o***o**o***

程序应该输出：
1

题解：
求要把初始状态的硬币翻成目标状态的最小操作步数，根据观察规律可以知道，只用遍历两个字符串，求两字符串中不相同的那个子串的长度，即最小操作步数，如**和oo两个字符串，其不相同的子串为字符下标为0和5之间的子串，长度为5，即最小操作步数为5，代码即求两个字符串中不相同的子串的长度。代码如下：

#include
#include
using namespace std;

int n, ans;
string src, target;

int main()
{
	cin >> src;
	cin >> target;
	n = src.length();
	for (int i = 0, start = -1; i < n; i ++)
	{
		if (src[i] != target[i])
		{
			if (start == -1)//如果没有标记过就标记为子串头 
				start = i;
			else//如果标记过就把子串长度加入答案，继续查找 
			{
				ans += (i - start);
				start = -1;
			}
		}
	}
	cout << ans << endl;
    return 0;
}

9 带分数

题目：

100 可以表示为带分数的形式：100 = 3 + 69258 / 714

还可以表示为：100 = 82 + 3546 / 197

注意特征：带分数中，数字1~9分别出现且只出现一次（不包含0）。

类似这样的带分数，100 有 11 种表示法。

题目要求： 从标准输入读入一个正整数N (N<1000*1000) 程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
注意：不要求输出每个表示，只统计有多少表示法！

例如：
用户输入：
100
程序输出：
11

再例如：
用户输入：
105
程序输出：
6

题解：
求一个数可表示为多少种带分数，该题主要思想在于数字1-9全排列，再向其中插入+和/，判断每一种情况是否达成等式，统计符合要求的数量。难点在于字符串的提取和字符串与整数的转化，需要用到substr()提取字符串，atoi()将字符串转化为整数，和全排列函数next_permutation(),具体代码及注释如下：

#include
#include
#include
#include
using namespace std;

int n, ans;
string src, target;
//substr()提取字符串，atoi()字符串转化为整数
//c_str()返回字符串的第一个字符地址，next_permutation() 
int main()
{
	int n;
	cin >> n;
	string s = "123456789";
	do{
		for (int i = 1; i <= 7; i ++)//+前的串的长度 
		{
			string a = s.substr(0, i);//提取s从头开始的i长度的字符串 
			int inta = atoi(a.c_str());//将字符串a转化为整数 
			if (inta >= n) continue;
			for (int j = i; j <= 9 - i - 1; j ++)//+和/之间串的长度 
			{
				string b = s.substr(i, j);//取s从i开始的j长度的字符串 
				string c = s.substr(i + j);//从i+j位开始提取后面所有字符串 
				int intb = atoi(b.c_str()); 
				int intc = atoi(c.c_str());//将字符串b、c转化为整数
				if (intb % intc == 0 && inta + intb / intc == n) ans ++;
			}
		}
	}while (next_permutation(s.begin(), s.end()));//全排列s 
	cout << ans << endl;
    return 0;
}

10 连号区间数

题目：

小明这些天一直在思考这样一个奇怪而有趣的问题：

在1~N的某个全排列中有多少个连号区间呢？这里所说的连号区间的定义是：

如果区间[L, R]里的所有元素（即此排列的第L个到第R个元素）递增排序后能得到一个长度为R-L+1的“连续”数列，则称这个区间连号区间。

当N很小的时候，小明可以很快地算出答案，但是当N变大的时候，问题就不是那么简单了，现在小明需要你的帮助。

输入格式： 第一行是一个正整数N (1 <= N <= 50000), 表示全排列的规模。 第二行是N个不同的数字Pi(1 <= Pi <=N)， 表示这N个数字的某一全排列。

输出格式： 输出一个整数，表示不同连号区间的数目。

示例：
用户输入：
4 3 2 4 1

程序应输出：
7

用户输入：
5 3 4 2 5 1

程序应输出：
9

解释：
第一个用例中，有7个连号区间分别是：[1,1], [1,2], [1,3], [1,4], [2,2], [3,3], [4,4]
第二个用例中，有9个连号区间分别是：[1,1], [1,2], [1,3], [1,4], [1,5], [2,2], [3,3],[4,4], [5,5]

题解：
因为连号区间内数字是连续的，则区间内最大值与最小值的差加一即为该区间长度，即该区间首尾下标相减再加一，则不断找出不同长短内的区间，判断其最大值与最小值之差与首尾下标之差是否相等即是否为连号区间，另外，首尾相同的区间也视为连号区间，则这两点就是遍历数组找连号区间的条件。代码如下：

#include
#include
using namespace std;

int n, ans;
int a[50000];

int main()
{
	cin >> n;
	for (int i = 0; i < n; i ++) cin >> a[i];
	for (int j = 0; j <= n - 1; j ++)
	{
		int min = a[j], max = a[j];
		for (int i = j; i <= n - 1; i ++)
		{
			if (a[i] > max) max = a[i];
			if (a[i] < min) min = a[i];
			if (i == j) ans ++;//首尾相同视为连号区间 
			else if (max - min + 1 == i - j + 1) ans ++;
			//最大值与最小值之差与首尾下标之差相同视为连号区间 
		}
	}
	cout << ans << endl;
    return 0;
}