Keypoint-Guided Optimal Transport阅读笔记
假设已经直到源域和目标域之间的某几个点的对应关系
公式
Σ m = { p ∈ R + m ∣ ∑ i p i = 1 } \Sigma_m=\left\{\mathbf{p}\in\mathbb{R}_+^m | \sum_i p_i = 1\right\} Σm={p∈R+m∣∑ipi=1}
π i , : \pi_{i,:} πi,:表示 π \mathbf{\pi} π的第 i i i行
π : , j \pi_{:,j} π:,j表示 π \mathbf{\pi} π的第 j j j列
⟨ P , Q ⟩ F = t r ( P T Q ) \left\langle \mathbf{P},\mathbf{Q}\right\rangle_F = \rm{tr}\left(\mathbf{P}^T\mathbf{Q}\right) ⟨P,Q⟩F=tr(PTQ)
Background on Optimal Transport
Kantorovich Problem (KP)
考虑两组数据
源: X = { x i } i = 1 m \mathbf{X} = \left\{x_i\right\}_{i=1}^m X={xi}i=1m
目标: Y = { y j } j = 1 n \mathbf{Y} = \left\{y_j\right\}_{j=1}^n Y={yj}j=1n
分布 p = ∑ i = 1 m p i δ x i \mathbf{p} = \sum_{i=1}^{m}p_i\delta_{x_i} p=∑i=1mpiδxi, q = ∑ j = 1 n p j δ y j \mathbf{q} = \sum_{j=1}^{n}p_j\delta_{y_j} q=∑j=1npjδyj
p ∈ Σ m , q ∈ Σ n \mathbf{p}\in \Sigma_m, \mathbf{q}\in \Sigma_n p∈Σm,q∈Σn
代价矩阵: C = ( C i , j ) ∈ R m × n \mathbf{C}=\left(C_{i,j}\right)\in\mathbb{R}^{m\times n} C=(Ci,j)∈Rm×n
其中, C i , j = c ( x i , y j ) C_{i,j}=c\left(x_i,y_j\right) Ci,j=c(xi,yj)
目标:将 p \mathbf{p} p转为 q \mathbf{q} q的最小代价
min π ∈ Π ( p , q ) L k p ( π ) ≜ ⟨ π , C ⟩ F , s.t. Π ( p , q ) = { π ∈ R + m × n ∣ π 1 n = p , π T 1 m = q } \min _{\pi \in \Pi(\mathbf{p}, \mathbf{q})} L_{k p}(\pi) \triangleq\langle\mathbf{\pi}, \mathbf{C}\rangle_F, \text { s.t. } \Pi(\mathbf{p}, \mathbf{q})=\left\{\mathbf{\pi} \in \mathbb{R}_{+}^{m \times n} \mid \mathbf{\pi} \mathbb{1}_n=\mathbf{p}, \mathbf{\pi}^T \mathbb{1}_m=\mathbf{q}\right\} π∈Π(p,q)minLkp(π)≜⟨π,C⟩F, s.t. Π(p,q)={π∈R+m×n∣π1n=p,πT1m=q}
Partial OT model
考虑只将 p \mathbf{p} p的部分转为 q \mathbf{q} q所需要的代价
例如只传输 s s s单位,其中 0 ≤ s ≤ min ( ∥ p ∥ 1 , ∥ q ∥ 1 ) 0\le s \le \min \left(\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\right) 0≤s≤min(∥p∥1,∥q∥1)
min π ∈ Π s ( p , q ) L k p ( π ) ≜ ⟨ π , C ⟩ F , s.t. Π s ( p , q ) = { π ∈ R + m × n ∣ π 1 n ≤ p , π T 1 m ≤ q , 1 m T π 1 n = s } \min _{\pi \in \Pi^s(\mathbf{p}, \mathbf{q})} L_{k p}(\pi) \triangleq\langle\mathbf{\pi}, \mathbf{C}\rangle_F, \text { s.t. } \Pi^s(\mathbf{p}, \mathbf{q})=\left\{\mathbf{\pi} \in \mathbb{R}_{+}^{m \times n} \mid \mathbf{\pi} \mathbb{1}_n\le \mathbf{p}, \mathbf{\pi}^T \mathbb{1}_m\le \mathbf{q}, \mathbb{1}_m^T\mathbf{\pi}\mathbf{1}_n=s\right\} π∈Πs(p,q)minLkp(π)≜⟨π,C⟩F, s.t. Πs(p,q)={π∈R+m×n∣π1n≤p,πT1m≤q,1mTπ1n=s}
注意这里 p \mathbf{p} p和 q \mathbf{q} q的量可以不一样
Gromov-Wasserstein (GW) model
x i x_i xi和 y j y_j yj可能不在一个空间里,(比如图片和声音)
GW model使用的是域内的距离,源域 C s = ( C i , k s ) ∈ R m × n \mathbf{C}^s=\left(C_{i,k}^s\right) \in \mathbb{R}^{m\times n} Cs=(Ci,ks)∈Rm×n,目标域 C t = ( C j , l t ) ∈ R n × n \mathbf{C}^t=\left(C_{j,l}^t\right)\in\mathbb{R}^{n\times n} Ct=(Cj,lt)∈Rn×n
其中 C i , k s C_{i,k}^s Ci,ks表示 x i x_i xi和 x k x_k xk的距离
C j , l t C_{j,l}^t Cj,lt表示 y j y_j yj和 y l y_l yl的距离
min π ∈ Π ( p , q ) L g w ( π ) ≜ ∑ i , k = 1 m ∑ j , l = 1 n π i , j π k , l ∣ C i , k s − C j , l t ∣ 2 \min\limits_{\mathbf{\pi}\in \Pi\left(\mathbf{p},\mathbf{q}\right)} L_{gw}\left(\mathbf{\pi}\right) \triangleq \sum_{i,k=1}^{m}\sum_{j,l=1}^n \pi_{i,j}\pi_{k,l}\left|C_{i,k}^s - C_{j,l}^t\right|^2 π∈Π(p,q)minLgw(π)≜i,k=1∑mj,l=1∑nπi,jπk,l Ci,ks−Cj,lt 2
Keypoint-Guided Optimal Transport
Preservation of Matching of Keypoints in Transport
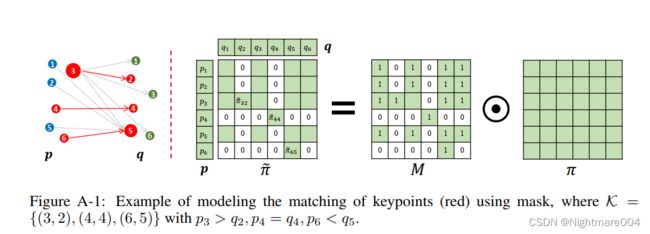
设关键点对 K = { ( i u , j u ) } u = 1 U \mathcal{K} = \left\{\left(i_u, j_u\right)\right\}_{u=1}^U K={(iu,ju)}u=1U
U U U表示关键点对数量
用 I = { i u } u = 1 U \mathcal{I} = \left\{i_u\right\}_{u=1}^{U} I={iu}u=1U和 J = { j u } u = 1 U \mathcal{J}=\left\{j_u\right\}_{u=1}^U J={ju}u=1U表示源域和目标域的关键点的索引
例如 K = { ( 3 , 2 ) , ( 6 , 5 ) } \mathcal{K}= \left\{\left(3,2\right), \left(6,5\right)\right\} K={(3,2),(6,5)},那么 I = { 3 , 6 } , J = { 2 , 5 } \mathcal{I} = \left\{3,6\right\},\mathcal{J} = \left\{2,5\right\} I={3,6},J={2,5}
作者首先保证这几个关键点能匹配上
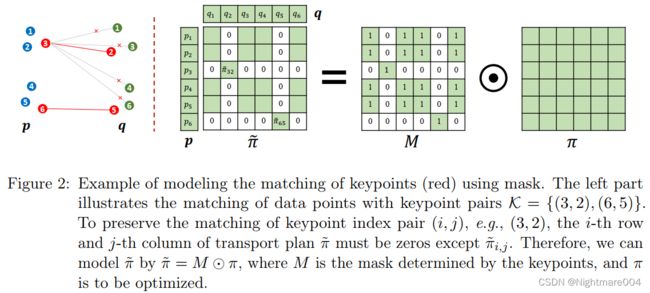
如果 ( i , j ) ∈ K \left(i,j\right)\in\mathcal{K} (i,j)∈K,则最优传输方案 π ~ \tilde{\mathbf{\pi}} π~的第 i i i行和第 j j j列除了 π ~ i , j \tilde{\mathbf{\pi}}_{i,j} π~i,j以外都为 0 0 0
(因为 x i x_i xi只能传输给 y j y_j yj)
π ~ = M ⊙ π \tilde{\mathbf{\pi}} = \mathbf{M}\odot \mathbf{\pi} π~=M⊙π
定义
Π ( p , q ; M ) = { π ∈ R + m × n ∣ ( M ⊙ π ) 1 n = p , ( M ⊙ π ) T 1 m = q } \Pi\left(\mathbf{p}, \mathbf{q};\mathbf{M}\right) = \left\{\mathbf{\pi} \in \mathbb{R}_+^{m\times n} | \left(\mathbf{M}\odot \mathbf{\pi}\right)\mathbb{1}_n = \mathbf{p}, \left(\mathbf{M}\odot \mathbf{\pi}\right)^T\mathbb{1}_m = \mathbf{q}\right\} Π(p,q;M)={π∈R+m×n∣(M⊙π)1n=p,(M⊙π)T1m=q}
其中
M i , j = { 1 , if ( i , j ) ∈ K , 0 , if i ∈ I and ( i , j ) ∉ K , 0 , if j ∈ J and ( i , j ) ∉ K , 1 , otherwise ( i.e., i ∉ I and j ∉ J ) M_{i, j}= \begin{cases}1, & \text { if }(i, j) \in \mathcal{K}, \\ 0, & \text { if } i \in \mathcal{I} \text { and }(i, j) \notin \mathcal{K}, \\ 0, & \text { if } j \in \mathcal{J} \text { and }(i, j) \notin \mathcal{K}, \\ 1, & \text { otherwise }(\text { i.e., } i \notin \mathcal{I} \text { and } j \notin \mathcal{J})\end{cases} Mi,j=⎩ ⎨ ⎧1,0,0,1, if (i,j)∈K, if i∈I and (i,j)∈/K, if j∈J and (i,j)∈/K, otherwise ( i.e., i∈/I and j∈/J)
注意,这里是假设如果 ( i , j ) ∈ K \left(i,j\right)\in\mathbb{K} (i,j)∈K,则 p i = q j p_i=q_j pi=qj
M i , j = { 1 , if ( i , j ) ∈ K , 0 , if i ∈ I , p i ≤ q κ ( i ) , and ( i , j ) ∉ K , 0 , if j ∈ J , p κ ′ ( j ) ≥ q j , and ( i , j ) ∉ K , 1 , if i ∈ I , p i > q κ ( i ) , and ( i , j ) ∉ K , 1 , if j ∈ J , p κ ′ ( j ) < q j , and ( i , j ) ∉ K , 1 , otherwise ( i.e. , i ∉ I , j ∉ J ) . M_{i, j}= \begin{cases}1, & \text { if }(i, j) \in \mathcal{K}, \\ 0, & \text { if } i \in \mathcal{I}, p_i \leq q_{\kappa(i)}, \text { and }(i, j) \notin \mathcal{K}, \\ 0, & \text { if } j \in \mathcal{J}, p_{\kappa^{\prime}(j)} \geq q_j, \text { and }(i, j) \notin \mathcal{K}, \\ 1, & \text { if } i \in \mathcal{I}, p_i>q_{\kappa(i)}, \text { and }(i, j) \notin \mathcal{K}, \\ 1, & \text { if } j \in \mathcal{J}, p_{\kappa^{\prime}(j)}
其中 j = κ ( i ) , i = κ ′ ( j ) j=\kappa\left(i\right), i=\kappa^{\prime}(j) j=κ(i),i=κ′(j),若 ( i , j ) ∈ K \left(i,j\right)\in\mathcal{K} (i,j)∈K
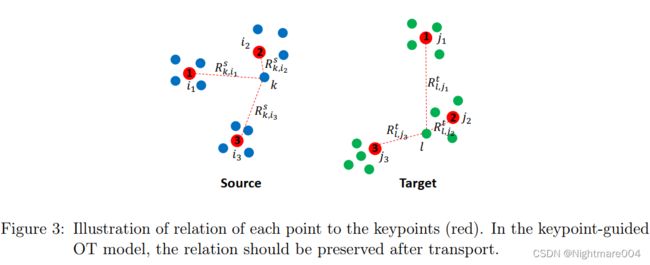
Modeling the Relation to Keypoints
对于 x k ∈ X x_k\in X xk∈X, 他到 x i u x_{i_u} xiu的关系分数定义为
R k , i u s = e − C k , i u s / τ ∑ u ′ = 1 U e − C k , i u ′ s / τ , ∀ i u ∈ I R_{k, i_u}^s=\frac{e^{-C_{k, i_u}^s / \tau}}{\sum_{u^{\prime}=1}^U e^{-C_{k, i_{u^{\prime}}}^s / \tau}}, \forall i_u \in \mathcal{I} Rk,ius=∑u′=1Ue−Ck,iu′s/τe−Ck,ius/τ,∀iu∈I
其中 τ = ρ max i , k { C i , k s } \tau = \rho \max_{i,k} \left\{C_{i,k}^s\right\} τ=ρmaxi,k{Ci,ks}
可以看出如果 x k x_k xk到最近的关键点的分数最大
类似地
对于 y l ∈ Y y_l\in Y yl∈Y, 他到 y j u y_{j_u} yju的关系分数定义为
R l , j u t = e − C l , j u t / τ ′ ∑ u ′ = 1 U e − C l , j u ′ t / τ ′ , ∀ j u ∈ J R_{l, j_u}^t=\frac{e^{-C_{l, j_u}^t / \tau^{\prime}}}{\sum_{u^{\prime}=1}^U e^{-C_{l, j_{u^{\prime}}}^t / \tau^{\prime}}}, \forall j_u \in \mathcal{J} Rl,jut=∑u′=1Ue−Cl,ju′t/τ′e−Cl,jut/τ′,∀ju∈J
其中 τ ′ = ρ max j , l { C j , l t } \tau^\prime = \rho \max_{j,l} \left\{C_{j,l}^t\right\} τ′=ρmaxj,l{Cj,lt}
这里 max \max max的目的是归一化,进而增加鲁棒性
ρ \rho ρ设置为 0.1 0.1 0.1,是一个常见的温度系数
R k s = ( R k , i 1 s , R k , i 2 s , ⋯ R k , i U s ) R_k^s = \left(R_{k,i_1}^s,R_{k,i_2}^s,\cdots R_{k,i_U}^s\right) Rks=(Rk,i1s,Rk,i2s,⋯Rk,iUs)
R l t = ( R l , j 1 t , R l , j 2 t , ⋯ R l , j U t ) R_l^t = \left(R_{l,j_1}^t,R_{l,j_2}^t,\cdots R_{l,j_U}^t\right) Rlt=(Rl,j1t,Rl,j2t,⋯Rl,jUt)
Realizing Keypoint Guidance by Relation Preservation
G = ( G k , l ) ∈ R m × n , G k , l = d ( R k s , R l t ) \mathbf{G} = \left(G_{k,l}\right)\in\mathbb{R}^{m\times n}, \quad G_{k,l} = d\left(R_{k}^s, R_l^t\right) G=(Gk,l)∈Rm×n,Gk,l=d(Rks,Rlt)
其中 d d d衡量 R k s R_k^s Rks和 R l t R_l^t Rlt的不相似度,如果 R k s R_k^s Rks和 R l t R_l^t Rlt相似,那么 G k , l G_{k,l} Gk,l非常小
这里 d d d设置为JS散度
KeyPoint-Guided model by ReLation preservation (KPG-RL) 定义为
min π ∈ Π ( p , q ; M ) L k p g ( π ) ≜ ⟨ M ⊙ π , G ⟩ F \min\limits_{\mathbf{\pi}\in\Pi\left(\mathbf{p},\mathbf{q};\mathbf{M}\right)} L_{kpg}\left(\mathbf{\pi}\right) \triangleq \left\langle \mathbf{M}\odot \mathbf{\pi}, \mathbf{G}\right\rangle_F π∈Π(p,q;M)minLkpg(π)≜⟨M⊙π,G⟩F
根据定义
1.对应的关键点会被强制匹配
2. G \mathbf{G} G较小的地方,最优传输方案中对应的位置就会越大
d ( R k s , R l t ) d\left(R_{k}^s, R_l^t\right) d(Rks,Rlt)基本取决于离得最近的关键点
求解:
求解可以用线性规划,也可以加入熵正则化用sinkhorn
u ( l + 1 ) = p K v ( l ) , v ( l + 1 ) = q K T u ( l + 1 ) \mathbf{u}^{\left(l+1\right)}=\frac{\mathbf{p}}{\mathbf{K}\mathbf{v}^{\left(l\right)}}, \quad \mathbf{v}^{\left(l+1\right)}=\frac{\mathbf{q}}{\mathbf{K}^T\mathbf{u}^{\left(l+1\right)}} u(l+1)=Kv(l)p,v(l+1)=KTu(l+1)q
其中 K = M ⊙ e − G / ε \mathbf{K} = \mathbf{M}\odot e^{-G/\varepsilon} K=M⊙e−G/ε
Imposing Keypoint Guidance in KP/GW
KPG-RL-KP
相当于加了个正则
min π ∈ Π ( p , q ; M ) { α L k p ( M ⊙ π ) + ( 1 − α ) L k p g ( π ) = ⟨ M ⊙ π , α C + ( 1 − α ) G ⟩ F } , α ∈ ( 0 , 1 ) \min\limits_{\mathbf{\pi} \in \Pi\left(\mathbf{p}, \mathbf{q};\mathbf{M}\right)} \left\{\alpha L_{kp}\left(\mathbf{M}\odot \mathbf{\pi}\right) +\left(1-\alpha\right) L_{kpg}\left(\mathbf{\pi}\right)=\left\langle \mathbf{M}\odot \mathbf{\pi}, \alpha \mathbf{C} +\left(1-\alpha\right)\mathbf{G}\right\rangle_F\right\}, \alpha \in \left(0,1\right) π∈Π(p,q;M)min{αLkp(M⊙π)+(1−α)Lkpg(π)=⟨M⊙π,αC+(1−α)G⟩F},α∈(0,1)
依然可以用线性规划或者sinkhorn算法求解
KPG-RL-GW
min π ∈ Π ( p , q ; M ) α L g w ( M ⊙ π ) + ( 1 − α ) L k p g ( π ) , α ∈ ( 0 , 1 ) \min\limits_{\mathbf{\pi} \in \Pi\left(\mathbf{p}, \mathbf{q};\mathbf{M}\right)}\alpha L_{gw}\left(\mathbf{M}\odot \mathbf{\pi}\right) +\left(1-\alpha\right) L_{kpg}\left(\mathbf{\pi}\right), \alpha \in \left(0,1\right) π∈Π(p,q;M)minαLgw(M⊙π)+(1−α)Lkpg(π),α∈(0,1)
依然用Frank-Walfe算法求解
Extension to Partial OT
min π ∈ Π s ( p , q ; M ) { L k p g ( M ⊙ π ) = ⟨ M ⊙ π , C ⟩ F } \min _{\pi \in \Pi^s(\mathbf{p}, \mathbf{q};\mathbf{M})} \left\{L_{k pg}(\mathbf{M}\odot\mathbf{\pi})=\langle \mathbf{M}\odot\mathbf{\pi}, \mathbf{C}\rangle_F\right\} π∈Πs(p,q;M)min{Lkpg(M⊙π)=⟨M⊙π,C⟩F}
其中
Π s ( p , q ; M ) = { π ∈ R + m × n ∣ ( M ⊙ π ) 1 n ≤ p , ( M ⊙ π ) T 1 m ≤ q , 1 m T ( M ⊙ π ) 1 n = s ; ( M ⊙ π ) i , : 1 n = p i , ∀ i ∈ I ; ( M ⊙ π ) : , j 1 m = p i , ∀ j ∈ J ; } \Pi^s\left(\mathbf{p},\mathbf{q};\mathbf{M}\right) = \left\{\mathbf{\pi}\in\mathbb{R}_+^{m\times n}| \left(\mathbf{M}\odot \mathbf{\pi}\right)\mathbf{1}_n\le \mathbf{p},\left(\mathbf{M}\odot \mathbf{\pi}\right)^T\mathbf{1}_m\le \mathbf{q},\mathbf{1}_m^T\left(\mathbf{M}\odot\mathbf{\pi}\right)\mathbf{1}_n=s; \left(\mathbf{M}\odot\mathbf{\pi}\right)_{i,:}\mathbf{1}_n=p_i,\forall i \in \mathcal{I}; \left(\mathbf{M}\odot\mathbf{\pi}\right)_{:,j}\mathbf{1}_m=p_i,\forall j \in \mathcal{J}; \right\} Πs(p,q;M)={π∈R+m×n∣(M⊙π)1n≤p,(M⊙π)T1m≤q,1mT(M⊙π)1n=s;(M⊙π)i,:1n=pi,∀i∈I;(M⊙π):,j1m=pi,∀j∈J;}
Chapel等人提出一种将partial ot转为ot的方法
增加dummy point,剩下的点传输给 dummy point

源域增加一个 ∥ q ∥ 1 − s \|\mathbf{q}\|_1-s ∥q∥1−s量的dummy point
目标域增加一个 ∥ p ∥ 1 − s \|\mathbf{p}\|_1-s ∥p∥1−s量的dummy point
令 p ˉ = ( p T , ∥ q ∥ 1 − s ) T \bar{\mathbf{p}} = \left(\mathbf{p}^T,\|\mathbf{q}\|_1-s\right)^T pˉ=(pT,∥q∥1−s)T
q ˉ = ( q T , ∥ p ∥ 1 − s ) T \bar{\mathbf{q}} = \left(\mathbf{q}^T,\|\mathbf{p}\|_1-s\right)^T qˉ=(qT,∥p∥1−s)T
G ˉ = [ G ξ 1 n ξ 1 m T 2 ξ + A ] , M ˉ = [ M a b T 1 ] \bar{\mathbf{G}} = \begin{bmatrix} \mathbf{G}& \xi\mathbf{1}_n\\ \xi \mathbf{1}_m^T& 2\xi + A \end{bmatrix}, \bar{\mathbf{M}} = \begin{bmatrix} \mathbf{M} & \mathbf{a}\\ \mathbf{b}^T & 1 \end{bmatrix} Gˉ=[Gξ1mTξ1n2ξ+A],Mˉ=[MbTa1]
其中 A > 0 , ξ A>0, \xi A>0,ξ是两个固定的标量, a i = 0 , ∀ i ∈ I a_i = 0,\forall i \in \mathcal{I} ai=0,∀i∈I,否则 a i = 1 a_i=1 ai=1
b j = 0 , ∀ j ∈ J b_j = 0,\forall j \in \mathcal{J} bj=0,∀j∈J,否则 b j = 1 b_j=1 bj=1
原问题转为
min π ˉ ∈ Π ( p ˉ , q ˉ ; M ˉ ) ⟨ M ˉ ⊙ π ˉ , G ˉ ⟩ F \min\limits_{\bar{\mathbf{\pi}} \in \Pi\left(\bar{\mathbf{p}},\bar{\mathbf{q}};\bar{\mathbf{M}}\right)}\left\langle \bar{\mathbf{M}}\odot \bar{\mathbf{\pi}}, \bar{\mathbf{G}}\right\rangle_F πˉ∈Π(pˉ,qˉ;Mˉ)min⟨Mˉ⊙πˉ,Gˉ⟩F
可以证明:假设 A > 0 , ∑ i ∈ I p i < s , ∑ j ∈ I q j < s A>0, \sum_{i\in\mathcal{I}} p_i A>0,∑i∈Ipi<s,∑j∈Iqj<s
则 M ˉ ⊙ π ˉ ∗ \bar{\mathbf{M}}\odot \bar{\mathbf{\pi}}^* Mˉ⊙πˉ∗的左上 m × n m\times n m×n矩阵就是 M ⊙ π ∗ \mathbf{M} \odot \mathbf{\pi}^* M⊙π∗
证明:
令 π ¨ = π ˉ 1 : m , 1 : n ∗ , t = π ˉ m + 1 , n + 1 ∗ \ddot{\mathbf{\pi}} = \bar{\mathbf{\pi}}_{1:m,1:n}^*, t = \bar{\mathbf{\pi}}_{m+1, n+1}^* π¨=πˉ1:m,1:n∗,t=πˉm+1,n+1∗
这个证明分为3步
1.证明 t = 0 t=0 t=0
2.证明 π ¨ ∈ Π s ( p , q ; M ) \ddot{\mathbf{\pi}} \in \Pi^s\left(\mathbf{p}, \mathbf{q}; \mathbf{M}\right) π¨∈Πs(p,q;M)
3.证明 M ⊙ π ¨ \mathbf{M} \odot \ddot{\mathbf{\pi}} M⊙π¨是最优解
因为 π ˉ ∗ ∈ Π ( p ˉ , q ˉ ; M ˉ ) , t = π ˉ m + 1 , n + 1 ∗ \bar{\mathbf{\pi}}^* \in \Pi\left(\bar{\mathbf{p}}, \bar{\mathbf{q}};\bar{\mathbf{M}}\right), t = \bar{\mathbf{\pi}}_{m+1, n+1}^* πˉ∗∈Π(pˉ,qˉ;Mˉ),t=πˉm+1,n+1∗,因此
1 m + 1 T ( M ˉ ⊙ π ˉ ∗ ) 1 n + 1 = [ 1 m T 1 ] ( [ M a b 1 ] ⊙ [ π ¨ π ˉ 1 : m , n + 1 ∗ π ˉ m + 1 , 1 : n ∗ π ˉ m + 1 , n + 1 ∗ ] ) [ 1 n 1 ] = 1 m T ( M ⊙ π ¨ ) 1 n + ∑ i = 1 m a i π ˉ i , n + 1 ∗ + ∑ j = 1 n b j π m + 1 , j ∗ + t \begin{aligned} \mathbf{1}_{m+1}^T\left(\bar{\mathbf{M}}\odot \bar{\mathbf{\pi}}^*\right)\mathbf{1}_{n+1} & = \begin{bmatrix} \mathbf{1}_m^T & 1\\ \end{bmatrix}\left(\begin{bmatrix} \mathbf{M} & \mathbf{a}\\ \mathbf{b} & 1\\ \end{bmatrix}\odot \begin{bmatrix} \ddot{\mathbf{\pi}} & \bar{\mathbf{\pi}}_{1:m, n +1}^*\\ \bar{\mathbf{\pi}}_{m+1, 1:n}^* & \bar{\mathbf{\pi}}_{m+1, n + 1}^* \end{bmatrix}\right)\begin{bmatrix} \mathbf{1}_n\\ 1\\ \end{bmatrix}\\ &= \mathbf{1}_m^T\left(\mathbf{M}\odot \ddot{\mathbf{\pi}}\right)\mathbf{1}_n + \sum_{i=1}^{m} a_i \bar{\mathbf{\pi}}_{i,n+1}^* + \sum_{j=1}^{n} b_j \mathbf{\pi}_{m+1,j}^* + t \end{aligned} 1m+1T(Mˉ⊙πˉ∗)1n+1=[1mT1]([Mba1]⊙[π¨πˉm+1,1:n∗πˉ1:m,n+1∗πˉm+1,n+1∗])[1n1]=1mT(M⊙π¨)1n+i=1∑maiπˉi,n+1∗+j=1∑nbjπm+1,j∗+t
并且
1 m + 1 T ( M ˉ ⊙ π ˉ ∗ ) 1 n + 1 = 1 m + 1 T p ˉ = ∥ p ˉ ∥ 1 = ∥ p ∥ 1 + ∥ q ∥ 1 − s \mathbf{1}_{m+1}^T\left(\bar{\mathbf{M}} \odot \bar{\mathbf{\pi}}^*\right)\mathbf{1}_{n+1} = \mathbf{1}_{m+1}^T\bar{\mathbf{p}} = \|\bar{\mathbf{p}}\|_1 = \|\mathbf{p}\|_1 + \|\mathbf{q}\|_1 -s 1m+1T(Mˉ⊙πˉ∗)1n+1=1m+1Tpˉ=∥pˉ∥1=∥p∥1+∥q∥1−s
∑ i = 1 m a i π ˉ i , n + 1 ∗ + t = q n + 1 = ∥ p ∥ 1 − s \sum_{i=1}^{m} a_i\bar{\mathbf{\pi}}_{i,n+1}^* + t = q_{n+1} = \|\mathbf{p}\|_1 - s i=1∑maiπˉi,n+1∗+t=qn+1=∥p∥1−s
∑ j = 1 n b j π ˉ m + 1 , j ∗ + t = p n + 1 = ∥ q ∥ 1 − s \sum_{j=1}^{n} b_j\bar{\mathbf{\pi}}_{m + 1, j}^* + t = p_{n+1} = \|\mathbf{q}\|_1 - s j=1∑nbjπˉm+1,j∗+t=pn+1=∥q∥1−s
因此
1 m + 1 T ( M ˉ ⊙ π ˉ ∗ ) 1 n + 1 = 1 m T ( M ⊙ π ¨ ) 1 n + ∥ p ∥ 1 + ∥ q ∥ 1 − 2 s − t = ∥ p ∥ 1 + ∥ q ∥ 1 − s \mathbf{1}_{m+1}^T\left(\bar{\mathbf{M}}\odot \bar{\mathbf{\pi}}^*\right)\mathbf{1}_{n+1} = \mathbf{1}_m^T\left(\mathbf{M}\odot \ddot{\mathbf{\pi}}\right)\mathbf{1}_n +\|\mathbf{p}\|_1 + \|\mathbf{q}\|_1 -2s -t = \|\mathbf{p}\|_1 + \|\mathbf{q}\|_1 -s 1m+1T(Mˉ⊙πˉ∗)1n+1=1mT(M⊙π¨)1n+∥p∥1+∥q∥1−2s−t=∥p∥1+∥q∥1−s
进而
1 m T ( M ⊙ π ¨ ) 1 n = s + t \mathbf{1}_m^T\left(\mathbf{M}\odot \ddot{\mathbf{\pi}}\right)\mathbf{1}_n = s + t 1mT(M⊙π¨)1n=s+t
第一步:证明 t = 0 t=0 t=0
⟨ M ˉ ⊙ π ˉ ∗ , G ⟩ = ∑ i = 1 m ∑ j = 1 n M i , j π ˉ i , j ∗ G i , j + ξ ∑ i = 1 m a i π ˉ i , n + 1 ∗ + ξ ∑ j = 1 n b j π ˉ m + 1 , j ∗ + ( 2 ξ + A ) π ˉ m + 1 , n + 1 ∗ = ∑ i = 1 m ∑ j = 1 n M i , j π ˉ i , j ∗ G i , j + ξ ( ∥ p ∥ 1 + ∥ q ∥ 1 − 2 s − 2 t ) + ( 2 ξ + A ) t = ∑ i = 1 m ∑ j = 1 n M i , j π ˉ i , j ∗ G i , j + ξ ( ∥ p ∥ 1 + ∥ q ∥ 1 − 2 s ) + A t \begin{aligned} \left\langle \bar{\mathbf{M}} \odot \bar{\mathbf{\pi}}^*, \mathbf{G}\right\rangle & = \sum_{i=1}^{m}\sum_{j=1}^{n} M_{i,j}\bar{\mathbf{\pi}}_{i,j}^* G_{i,j} + \xi \sum_{i=1}^{m}a_i\bar{\mathbf{\pi}}_{i,n+1}^*\\ &+\xi \sum_{j=1}^{n} b_j \bar{\mathbf{\pi}}_{m+1,j}^* + \left(2\xi + A\right) \bar{\mathbf{\pi}}_{m+1, n + 1}^*\\ &= \sum_{i=1}^{m}\sum_{j=1}^{n} M_{i,j}\bar{\mathbf{\pi}}_{i,j}^* G_{i,j} + \xi\left(\|\mathbf{p}\|_1 + \|\mathbf{q}\|_1 -2s -2t\right) + \left(2\xi + A\right)t \\ &= \sum_{i=1}^{m}\sum_{j=1}^{n} M_{i,j}\bar{\mathbf{\pi}}_{i,j}^* G_{i,j} + \xi\left(\|\mathbf{p}\|_1 + \|\mathbf{q}\|_1 -2s\right) + At \\ \end{aligned} ⟨Mˉ⊙πˉ∗,G⟩=i=1∑mj=1∑nMi,jπˉi,j∗Gi,j+ξi=1∑maiπˉi,n+1∗+ξj=1∑nbjπˉm+1,j∗+(2ξ+A)πˉm+1,n+1∗=i=1∑mj=1∑nMi,jπˉi,j∗Gi,j+ξ(∥p∥1+∥q∥1−2s−2t)+(2ξ+A)t=i=1∑mj=1∑nMi,jπˉi,j∗Gi,j+ξ(∥p∥1+∥q∥1−2s)+At
假设 t > 0 t > 0 t>0, 那接下来就要构造一个可行解 γ \mathbf{\gamma} γ,满足 γ m + 1 , n + 1 = 0 \gamma_{m+1,n+1}=0 γm+1,n+1=0来形成矛盾
随机选择一个集合 S = { ( i , j ) ∣ π ˉ i , j ∗ > 0 , i ≤ m , j ≤ n , i ∉ I , j ∉ J } S = \left\{\left(i,j\right)| \bar{\mathbf{\pi}}_{i,j}^* >0,i \le m, j \le n, i\notin \mathcal{I}, j \notin \mathcal{J}\right\} S={(i,j)∣πˉi,j∗>0,i≤m,j≤n,i∈/I,j∈/J}
以及一对索引 ( i 0 , j 0 ) \left(i_0,j_0\right) (i0,j0),满足 S S S中的约束,使得 ∑ ( i , j ) ∈ S π ˉ i , j ∗ ≤ t \sum\limits_{\left(i,j\right)\in S}\bar{\mathbf{\pi}}_{i,j}^* \le t (i,j)∈S∑πˉi,j∗≤t以及 ∑ ( i , j ) ∈ S π ˉ i , j ∗ + π i 0 , j 0 ∗ > t \sum\limits_{\left(i,j\right)\in S}\bar{\mathbf{\pi}}_{i,j}^* + \mathbf{\pi}_{i_0,j_0}^* >t (i,j)∈S∑πˉi,j∗+πi0,j0∗>t
这样的 S S S和 ( i 0 , j 0 ) \left(i_0,j_0\right) (i0,j0)是一定存在的,因为
1 m T ( M ⊙ π ¨ ) 1 n = ∑ i = 1 m ∑ j = 1 n M i , j π ˉ i , j ∗ = ∑ i ∈ I , j M i , j π ˉ i , j ∗ + ∑ i ∉ I , j ∈ J M i , j π ˉ i , j ∗ + ∑ i ∉ I , j ∉ J M i , j π ˉ i , j ∗ = ∑ i ∈ I p i + ∑ i ∉ I , j ∉ J π ˉ i , j ∗ \begin{aligned} \mathbf{1}_m^T\left(\mathbf{M}\odot \ddot{\mathbf{\pi}}\right)\mathbf{1}_n &= \sum_{i=1}^{m} \sum_{j=1}^{n}M_{i,j}\bar{\mathbf{\pi}}_{i,j}^*\\ &= \sum_{i\in \mathcal{I},j} M_{i,j}\bar{\mathbf{\pi}}_{i,j}^* + \sum_{i\notin \mathcal{I},j\in \mathcal{J}} M_{i,j}\bar{\mathbf{\pi}}_{i,j}^* + \sum_{i\notin \mathcal{I},j\notin \mathcal{J}} M_{i,j}\bar{\mathbf{\pi}}_{i,j}^*\\ &=\sum_{i\in \mathcal{I}}p_i + \sum_{i\notin \mathcal{I},j\notin \mathcal{J}} \bar{\mathbf{\pi}}_{i,j}^*\\ \end{aligned} 1mT(M⊙π¨)1n=i=1∑mj=1∑nMi,jπˉi,j∗=i∈I,j∑Mi,jπˉi,j∗+i∈/I,j∈J∑Mi,jπˉi,j∗+i∈/I,j∈/J∑Mi,jπˉi,j∗=i∈I∑pi+i∈/I,j∈/J∑πˉi,j∗
由 1 m T ( M ⊙ π ¨ ) 1 n = s + t \mathbf{1}_{m}^T \left(\mathbf{M} \odot \ddot{\mathbf{\pi}}\right)\mathbf{1}_n = s+t 1mT(M⊙π¨)1n=s+t以及 ∑ i ∈ I p i < s \sum\limits_{i\in \mathcal{I}} p_i < s i∈I∑pi<s, 有 ∑ i ∉ I , j ∉ J π ˉ i , j ∗ > t \sum_{i\notin \mathcal{I},j\notin \mathcal{J}} \bar{\mathbf{\pi}}_{i,j}^* > t ∑i∈/I,j∈/Jπˉi,j∗>t
现在构造 γ \mathbf{\gamma} γ
∀ ( i , j ) ∈ S \forall \left(i,j\right) \in S ∀(i,j)∈S,令 γ i , j = 0 , γ i , n + 1 = π ˉ i , n + 1 ∗ + π ˉ i , j ∗ , γ m + 1 , j = π ˉ m + 1 , j ∗ + π ˉ i , j ∗ \gamma_{i,j} = 0, \gamma_{i,n + 1} = \bar{\mathbf{\pi}}_{i, n + 1}^* + \bar{\mathbf{\pi}}_{i,j}^*,\gamma_{m+1, j} = \bar{\mathbf{\pi}}_{m+1, j}^* + \bar{\mathbf{\pi}}_{i,j}^* γi,j=0,γi,n+1=πˉi,n+1∗+πˉi,j∗,γm+1,j=πˉm+1,j∗+πˉi,j∗
γ i 0 , j 0 = π ˉ i 0 , j 0 ∗ − ( t − ∑ i ∉ I , j ∉ J π ˉ i , j ∗ ) , γ i 0 , n + 1 = π ˉ i 0 , n + 1 ∗ − ( t − ∑ i ∉ I , j ∉ J π ˉ i , j ∗ ) , γ m + 1 , j 0 = π ˉ m + 1 , j 0 ∗ − ( t − ∑ i ∉ I , j ∉ J π ˉ i , j ∗ ) \gamma_{i_0, j_0} = \bar{\mathbf{\pi}}_{i_0, j_0}^* - \left(t - \sum\limits_{i\notin \mathcal{I},j\notin \mathcal{J}} \bar{\mathbf{\pi}}_{i,j}^*\right), \gamma_{i_0, n+1} = \bar{\mathbf{\pi}}_{i_0, n+1}^* - \left(t - \sum\limits_{i\notin \mathcal{I},j\notin \mathcal{J}} \bar{\mathbf{\pi}}_{i,j}^*\right), \gamma_{m+1, j_0} = \bar{\mathbf{\pi}}_{m + 1, j_0}^* - \left(t - \sum\limits_{i\notin \mathcal{I},j\notin \mathcal{J}} \bar{\mathbf{\pi}}_{i,j}^*\right) γi0,j0=πˉi0,j0∗−(t−i∈/I,j∈/J∑πˉi,j∗),γi0,n+1=πˉi0,n+1∗−(t−i∈/I,j∈/J∑πˉi,j∗),γm+1,j0=πˉm+1,j0∗−(t−i∈/I,j∈/J∑πˉi,j∗)
∀ ( i , j ) ∉ S , γ i , j = π ˉ i , j ∗ , γ i , n + 1 = π ˉ i , n + 1 ∗ , γ m + 1 , j = π ˉ m + 1 , j ∗ \forall \left(i,j\right) \notin S, \gamma_{i,j} = \bar{\mathbf{\pi}}_{i,j}^*, \gamma_{i,n+1} = \bar{\mathbf{\pi}}_{i, n + 1}^*, \gamma_{m+1, j} = \bar{\mathbf{\pi}}_{m+1,j}^* ∀(i,j)∈/S,γi,j=πˉi,j∗,γi,n+1=πˉi,n+1∗,γm+1,j=πˉm+1,j∗
容易验证 γ ∈ Π ( p ˉ , q ˉ ; M ˉ ) \mathbf{\gamma} \in \Pi \left(\bar{\mathbf{p}}, \bar{\mathbf{q}};\bar{\mathbf{M}}\right) γ∈Π(pˉ,qˉ;Mˉ)
于是
⟨ M ˉ ⊙ γ , G ⟩ = ∑ i = 1 m ∑ j = 1 n M i , j γ i , j G i , j + ξ ( ∥ p ∥ 1 + ∥ q ∥ 1 − 2 s ) \left\langle \bar{\mathbf{M}} \odot \mathbf{\gamma}, \mathbf{G}\right\rangle = \sum_{i=1}^{m}\sum_{j=1}^{n} M_{i,j}\mathbf{\gamma}_{i,j} G_{i,j} + \xi\left(\|\mathbf{p}\|_1 + \|\mathbf{q}\|_1 -2s\right) ⟨Mˉ⊙γ,G⟩=i=1∑mj=1∑nMi,jγi,jGi,j+ξ(∥p∥1+∥q∥1−2s)
利用 M ˉ ⊙ π ˉ ∗ \bar{\mathbf{M}} \odot \bar{\mathbf{\pi}}^* Mˉ⊙πˉ∗的最优性,有
⟨ M ˉ ⊙ γ , G ⟩ − ⟨ M ˉ ⊙ π ˉ ∗ , G ⟩ = ∑ i = 1 m ∑ j = 1 n M i , j ( γ i , j − π ˉ i , j ∗ ) G i , j − A t > 0 \left\langle \bar{\mathbf{M}} \odot \mathbf{\gamma}, \mathbf{G}\right\rangle - \left\langle \bar{\mathbf{M}} \odot \bar{\mathbf{\pi}}^*, \mathbf{G}\right\rangle = \sum_{i=1}^{m} \sum_{j=1}^{n}M_{i,j}\left(\mathbf{\gamma}_{i,j} - \bar{\mathbf{\pi}}_{i,j}^*\right)G_{i,j} - At > 0 ⟨Mˉ⊙γ,G⟩−⟨Mˉ⊙πˉ∗,G⟩=i=1∑mj=1∑nMi,j(γi,j−πˉi,j∗)Gi,j−At>0
由 γ \mathbf{\gamma} γ的定义, γ i , j ≤ π ˉ i , j ∗ \gamma_{i,j} \le \bar{\mathbf{\pi}}_{i,j}^* γi,j≤πˉi,j∗
因此 ∑ i = 1 m ∑ j = 1 n M i , j ( γ i , j − π ˉ i , j ∗ ) G i , j ≤ 0 \sum_{i=1}^{m} \sum_{j=1}^{n}M_{i,j}\left(\mathbf{\gamma}_{i,j} - \bar{\mathbf{\pi}}_{i,j}^*\right)G_{i,j}\le 0 ∑i=1m∑j=1nMi,j(γi,j−πˉi,j∗)Gi,j≤0, 进而矛盾
因此 t = 0 t=0 t=0
第二步:证明 π ¨ ∈ Π s ( p , q ; M ) \ddot{\mathbf{\pi}} \in \Pi^s\left(\mathbf{p}, \mathbf{q}; \mathbf{M}\right) π¨∈Πs(p,q;M)
(1) π ˉ ∗ ≥ 0 \bar{\mathbf{\pi}}^*\ge 0 πˉ∗≥0,因此 π ¨ ≥ 0 \ddot{\mathbf{\pi}} \ge 0 π¨≥0
(2) ( M ˉ ⊙ π ˉ ∗ ) 1 n + 1 = [ M ⊙ π ¨ a ⊙ π ˉ 1 : m , n + 1 ∗ b ⊙ π ˉ m + 1 , 1 : n ∗ 0 ] [ 1 n 1 ] = [ p ∥ q ∥ 1 − s ] \left(\bar{\mathbf{M}} \odot \bar{\mathbf{\pi}}^*\right) \mathbf{1}_{n+1} = \begin{bmatrix} \mathbf{M} \odot \ddot{\mathbf{\pi}}& \mathbf{a} \odot \bar{\mathbf{\pi}}_{1:m, n+1}^*\\ \mathbf{b}\odot \bar{\mathbf{\pi}}_{m+1, 1:n}^*& 0 \end{bmatrix}\begin{bmatrix}\mathbf{1}_n\\1\\\end{bmatrix} = \begin{bmatrix}\mathbf{p}\\\|\mathbf{q}\|_1 - s\end{bmatrix} (Mˉ⊙πˉ∗)1n+1=[M⊙π¨b⊙πˉm+1,1:n∗a⊙πˉ1:m,n+1∗0][1n1]=[p∥q∥1−s]
因此 ( M ⊙ π ¨ ) 1 n + a ⊙ π ˉ 1 : m , n + 1 ∗ = p \left(\mathbf{M}\odot\ddot{\mathbf{\pi}}\right)\mathbf{1}_n + \mathbf{a} \odot \bar{\mathbf{\pi}}_{1:m, n+1}^* = \mathbf{p} (M⊙π¨)1n+a⊙πˉ1:m,n+1∗=p,进而 ( M ⊙ π ¨ ) 1 n ≤ p \left(\mathbf{M}\odot\ddot{\mathbf{\pi}}\right)\mathbf{1}_n \le \mathbf{p} (M⊙π¨)1n≤p
(3)与上面类似, ( M ˉ ⊙ π ˉ ∗ ) T 1 m + 1 = ( q T , ∥ q ∥ 1 − s ) T \left(\bar{\mathbf{M}} \odot \bar{\mathbf{\pi}}^*\right)^T\mathbf{1}_{m+1} = \left(\mathbf{q}^T, \|\mathbf{q}\|_1-s\right)^T (Mˉ⊙πˉ∗)T1m+1=(qT,∥q∥1−s)T,因此 ( M ⊙ π ¨ ) T 1 m ≤ q \left(\mathbf{M}\odot\ddot{\mathbf{\pi}}\right)^T\mathbf{1}_m \le \mathbf{q} (M⊙π¨)T1m≤q
(4) 1 m T ( M ⊙ π ¨ ) 1 n = s + t = s \mathbf{1}_m^T\left(\mathbf{M}\odot \ddot{\mathbf{\pi}}\right)\mathbf{1}_n=s + t = s 1mT(M⊙π¨)1n=s+t=s
(5) ∀ i ∈ I , ( M ˉ ⊙ π ˉ ∗ ) i , : 1 n + 1 = ( M ⊙ π ¨ ) i , : 1 n + a i ⊙ π ˉ i , n + 1 ∗ = p i \forall i \in \mathcal{I}, \left(\bar{\mathbf{M}}\odot \bar{\mathbf{\pi}}^*\right)_{i,:}\mathbf{1}_{n+1} = \left(\mathbf{M}\odot\ddot{\mathbf{\pi}}\right)_{i,:}\mathbf{1}_n + \mathbf{a}_i \odot \bar{\mathbf{\pi}}_{i, n+1}^* = p_i ∀i∈I,(Mˉ⊙πˉ∗)i,:1n+1=(M⊙π¨)i,:1n+ai⊙πˉi,n+1∗=pi,又因为 a i = 0 a_i=0 ai=0,因此 ( M ⊙ π ¨ ) i , : 1 n = p i \left(\mathbf{M}\odot\ddot{\mathbf{\pi}}\right)_{i,:}\mathbf{1}_n = p_i (M⊙π¨)i,:1n=pi
(6) ∀ j ∈ J , 1 m + 1 T ( M ˉ ⊙ π ˉ ∗ ) : , j = 1 m T ( M ⊙ π ¨ ) : , j + b j ⊙ π ˉ m + 1 , j ∗ = q j \forall j \in \mathcal{J}, \mathbf{1}_{m+1}^T\left(\bar{\mathbf{M}}\odot \bar{\mathbf{\pi}}^*\right)_{:,j} = \mathbf{1}_m^T\left(\mathbf{M}\odot\ddot{\mathbf{\pi}}\right)_{:,j} + \mathbf{b}_j \odot \bar{\mathbf{\pi}}_{m+1,j}^* = q_j ∀j∈J,1m+1T(Mˉ⊙πˉ∗):,j=1mT(M⊙π¨):,j+bj⊙πˉm+1,j∗=qj,又因为 b j = 0 b_j=0 bj=0,因此 1 m T ( M ⊙ π ¨ ) : , j = q j \mathbf{1}_m^T\left(\mathbf{M}\odot\ddot{\mathbf{\pi}}\right)_{:,j} = q_j 1mT(M⊙π¨):,j=qj
因此 π ¨ ∈ Π s ( p , q ; M ) \ddot{\mathbf{\pi}} \in \Pi^s\left(\mathbf{p}, \mathbf{q}; \mathbf{M}\right) π¨∈Πs(p,q;M)
第三步:证明 M ⊙ π ¨ \mathbf{M} \odot \ddot{\mathbf{\pi}} M⊙π¨是最优解
假设有一个更优解 M ⊙ γ \mathbf{M}\odot\mathbf{\gamma} M⊙γ,其中 γ ∈ Π s ( p , q ; M ) \mathbf{\gamma} \in \Pi^s\left(\mathbf{p},\mathbf{q};\mathbf{M}\right) γ∈Πs(p,q;M),
∑ i = 1 m ∑ j = 1 n M i , j γ i , j G i , j < ∑ i = 1 m ∑ j = 1 n M i , j π ¨ i , j G i , j \sum_{i=1}^{m}\sum_{j=1}^{n}M_{i,j}\gamma_{i,j}G_{i,j} <\sum_{i=1}^{m}\sum_{j=1}^{n}M_{i,j}\ddot{\mathbf{\pi}}_{i,j}G_{i,j} i=1∑mj=1∑nMi,jγi,jGi,j<i=1∑mj=1∑nMi,jπ¨i,jGi,j
构造 γ ˉ \bar{\mathbf{\gamma}} γˉ,其中
i ≤ m , j ≤ n i\le m, j \le n i≤m,j≤n时, γ ˉ i , j = γ i , j \bar{\mathbf{\gamma}}_{i,j} = \gamma_{i,j} γˉi,j=γi,j
∀ i ≤ m \forall i \le m ∀i≤m,有 γ ˉ i , n + 1 = p i − ∑ j = 1 n γ i , j \bar{\gamma}_{i,n+1} = p_i - \sum\limits_{j=1}^{n}\gamma_{i,j} γˉi,n+1=pi−j=1∑nγi,j
∀ j ≤ n \forall j \le n ∀j≤n,有 γ ˉ m + 1 , j = q j − ∑ i = 1 n γ i , j \bar{\gamma}_{m+1, j} = q_j - \sum\limits_{i=1}^{n} \gamma_{i,j} γˉm+1,j=qj−i=1∑nγi,j
γ ˉ m + 1 , n + 1 = 0 \bar{\gamma}_{m+1, n+1} = 0 γˉm+1,n+1=0
容易验证, γ ˉ ∈ Π ( p ˉ , q ˉ ; M ˉ ) \bar{\gamma} \in \Pi\left(\bar{\mathbf{p}}, \bar{\mathbf{q}}; \bar{\mathbf{M}}\right) γˉ∈Π(pˉ,qˉ;Mˉ)
同时
⟨ M ˉ ⊙ γ ˉ , G ˉ ⟩ = ∑ i = 1 m ∑ j = 1 n M i , j γ i , j C i , j + ξ ( ∥ p ∥ 1 + ∥ q ∥ 1 − 2 s ) < ∑ i = 1 m ∑ j = 1 n M i , j π ¨ i , j G i , j + ξ ( ∥ p ∥ 1 + ∥ q ∥ 1 − 2 s ) = ⟨ M ˉ ⊙ π ˉ ∗ , G ˉ ⟩ \begin{aligned} \left\langle\bar{M} \odot \bar{\gamma}, \bar{G}\right\rangle & =\sum_{i=1}^m \sum_{j=1}^n M_{i, j} \gamma_{i, j} C_{i, j}+\xi\left(\|\boldsymbol{p}\|_1+\|\boldsymbol{q}\|_1-2 s\right) \\ & <\sum_{i=1}^m \sum_{j=1}^n M_{i, j} \ddot{\pi}_{i, j} G_{i, j}+\xi\left(\|\boldsymbol{p}\|_1+\|\boldsymbol{q}\|_1-2 s\right)=\left\langle\bar{M} \odot \bar{\pi}^*, \bar{G}\right\rangle \end{aligned} ⟨Mˉ⊙γˉ,Gˉ⟩=i=1∑mj=1∑nMi,jγi,jCi,j+ξ(∥p∥1+∥q∥1−2s)<i=1∑mj=1∑nMi,jπ¨i,jGi,j+ξ(∥p∥1+∥q∥1−2s)=⟨Mˉ⊙πˉ∗,Gˉ⟩
与 π ˉ ∗ \bar{\pi}^* πˉ∗最优矛盾