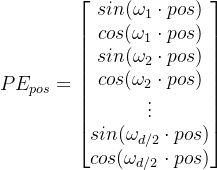一文搞懂Transformer的边角料知识：位置编码
目录
一、为什么需要位置编码
二、位置编码分类
1.表格型
2.函数型
三、Transformer的位置编码
1.位置编码应有的特点
2.Transformer的位置编码公式
3.三角函数
4.线性相关
5.相对位置关系
四、总结
一、为什么需要位置编码
在Transformer出现以前，NLP任务大多是以RNN、LSTM为代表的循环处理方式，即一个token一个token的输入到模型当中。模型本身是一种顺序结构，天生就包含了token在序列中的位置信息。但是这种模型有很多天生的缺陷，比如：
1.会出现“遗忘”的现象，无法支持长时间序列，虽然LSTM在一定程度上缓解了这种显现，但是这种缺陷仍然存在；
2.句子越靠后的token对结果的影响越大；
3.只能利用上文信息，不能获取下文信息；
4.计算的时间复杂度比较高，循环网络是一个token一个token的输入的，也就是句子有多长就要循环多少遍；
为了解决上述问题，Transformer出现了，Transformer将一哥token序列一次性输入到模型，不使用循环的形式。因为是一次性接收所有token作为输入进行并行处理，“遗忘”的问题没有了、所有的token都一视同仁了、上下文的信息能同时获取到、时间复杂度也降下来了。但是这又出现了新的问题，因为所有token一视同仁了，模型就没有办法知道每个token在句子中的相对和绝对的位置信息，而位置关系对于NLP任务来说是有着决定性影响的。比如下面的两句话token完全一样，但含义截然相反：
1.我把小姐姐按在地上摩擦
2.小姐姐把我按在地上摩擦
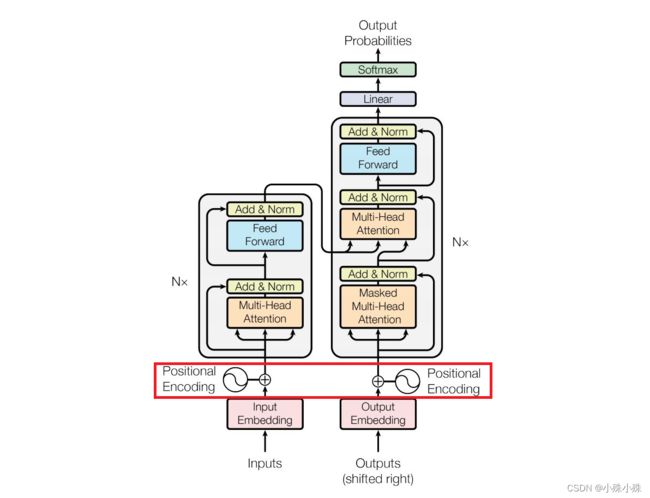
为了解决这个问题，Transformer把token的顺序信号加到词向量上帮助模型学习这些信息，这就位置编码（Positional Encoding）。下面这张图不用解释，大家再熟悉不过，接下来的内容不会涉及Self-Attention等牛逼的创新设计，只讨论位置编码，也就是红框的内容。
二、位置编码分类
位置编码用来标记token的前后顺序，总的来说，位置编码分为两个类型：表格型和函数型。
1.表格型
表格型位置编码就是建立一个长度为L的词表，按词表的长度来分配位置id。
最简单的想法就是从1开始向后排列，我们使用单字分词，如：
我 把 小 姐 姐 按 在 地 上 摩 擦
1 2 3 4 5 6 7 8 9 10 11
但是这种方式存在很大的问题，句子越长，后面的值越大，数字越大说明这个位置占的权重也越大，这样的方式无法凸显每个位置的真实的权重。
当然可以将上述编码进行归一化然后组成等差数列，但是这种方式也有问题，当句子长度不一样，每个位置的编码尺度不同，也就是说不同长度的句子，同一位置的编码是不一样的，如下面两句话：
我 把 小 姐 姐 按 在 地 上 摩 擦
0.09 0.18 0.27 0.36 0.45 0.54 0.63 0.72 0.81 0.9 0.99
看 你 往 哪 跑
0.2 0.4 0.6 0.8 1.0
2.函数型
函数型位置编码通过输入token的位置信息，得到相应的位置编码。这种方式并不使用上述绝对位置关系，而是使用相对位置的关系。
可以看到，使用相对位置的方法，我们可以清晰的知道单词之间的距离远近的关系，单独看某一个token的位置编码可能不知所谓，但是放在整个token序列中，就能表征token的相对位置关系。
比如下面这句话，我站在“按”字的位置，计算其它字距离“按”的相对距离，有正负可以区分前后：
我 把 小 姐 姐 按 在 地 上 摩 擦
-5 -4 -3 -2 -1 0 1 2 3 4 5
上面的句子只是一个演示，真实情况不会是这样。我要说明的是，相对位置编码需要线性相关，Transformer的位置编码就属于这种类型。
三、Transformer的位置编码
1.位置编码应有的特点
好的位置编码应该有如下特点：
1.每个时间步都有唯一的编码。
2.在不同长度的句子中，两个时间步之间的距离应该一致。
3.模型不受句子长短的影响，并且编码范围是有界的。（不会随着句子加长数字就无限增大）
4.同一时间序列中，每个连续的编码应该是等步长的，即线性相关的。
5.位置编码应该能表示token的绝对或相对位置关系。
下面我们就来看一下Transformer的位置编码，是否符合上面几点要求。
2.Transformer的位置编码公式
使用正余弦函数表示绝对位置，通过两者乘积得到相对位置：
（1）
（1）
其中PE表示位置编码；
表示一句话中token的位置；每个token的位置编码是一个向量（或者叫embedding），i表示这个向量中每个元素的index；
表示位置编向量的维度。
式1，其实是一个式子，看起来非常复杂，写的直观一点是下面这个样子：
（2）
其中
,可以看到，每个位置编码向量都是sin和cos交替。
3.三角函数
从式（2）中可以发现Transformer的位置编码使用了三角函数，三角函数是周期函数，那为什么要把每个维度设计成周期形式呢，可以看下面这个图，二进制格式表示一个数字：
| 十进制 | 二进制 | |||
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
可以看到以列为单位，不同位置上的数字都会出现0、1的交替变化。规律是第i位置上第
个数据交替一次。比如第0列（右面数第一列）是每1次都切换，第1列（右面数第二列）是每两次切换。但是在浮点数的世界中使用二进制值是对空间的浪费，所以我们可以用正弦函数代替。事实上，正弦函数也能表示出二进制那样的交替。随着波长的变长，带来的是数据变化的变慢，就如同上面的提到的。
Transformer的位置编码选择三角函数的官方解释是这样的：
位置编码的每个维度都对应于一个正弦曲线。波长形成一个从2π到10000·2π的几何轨迹。我们之所以选择这个函数，是因为我们假设它可以让模型很容易地通过相对位置进行学习，因为对于任何固定的偏移量k,PEpos+k都可以表示为PEpos的线性函数。
也就是说，每个维度都是波长不同的正弦波，波长范围是2π到10000·2π，选用10000这个比较大的数是因为三件函数式有周期的，在这个范围基本上，就不会出现波长一样的情况了。然后谷歌的科学家们为了让PE值的周期更长，还交替使用sin/cos来计算PE的值，就得到了最终的公式（1）。
下图可以比较清晰的表现这过程。相同颜色的是同一个token的词向量，为了方便展示，波形图只使用sin，而且波形图只是展示使用，并不是实际波形图：
可以看到，每个维度（即每一行）都是三角函数的波形，随着pos的增加，波长越来越长，这就很好的实现了低位变化快、高位变化慢的情况。那每个pos内（即每一列）的元素是否为线性相关呢？
4.线性相关
我们知道某一个token的位置是pos，如果某一个token表示为 pos+k ，那就表明这个位置距上一个token为k。
如果这时我们需要看看一个位置pos和pos+k 这两个token的关系。按照位置编码的的公式，我们可以计算pos+k 的位置编码，其结果如下：
（3）
（3）
因为
(4）
（4）
所以
（5）
（5）
将式（1）中的
用
代替，得到：
（6）
（6）
将式（6）带入式子（5），得到：
（7）
（7）
因为k是一个常数，所有上面公式中sin() 和cos() 的计算值也是常数，可以表示为：
（8）
（8）
这样，就可以将
写成矩阵乘法的形式：
（9）
至此可以发现，位置 pos的编码与位置pos+k的位置编码是线性关系。
那么问题来了，上面的推导过程可以看到线性关系，那怎么表示每个token的相对距离关系呢？
5.相对位置关系
我们将
和相乘 (两个向量的内积)，可以得到如下结果：
（10）
我们发现相乘后的结果为一个余弦的加和。这里影响值的因素就是k 。如果两个token的距离越大，也就是K越大，根据余弦函数的性质可以知道，两个位置的PE相乘结果越小。这样的关系可以得到，如果两个token距离越远则乘积的结果越小，所以位置编码可以表示相对位置关系。
四、总结
问我们上面提到了位置编码应该有的特点，我们再总结一下，Transformer的位置编码简称PE：
1.每个时间步都有唯一的编码：根据公式（1），是确定的，根据pos和i能计算出确定的值，这一点无疑是符合的；
2.在不同长度的句子中，两个时间步之间的距离应该一致：根据公式（1），（词向量的长度）是一个定值，原版Transform的512，所以就算输入句子长度不一样，到计算编码这一步，两个时间步之间的距离也是一致的；
3.编码范围是有界的。（不会随着句子加长数字就无限增大）：PE使用三角函数，振幅是1，所以范围是[-1,1]；
4.同一时间序列中，每个连续的编码应该是等步长的，即线性相关的：根据上一节的推导过程可以证明；
5.位置编码应该能表示token的绝对或相对位置关系：任意两个位置的token距离与PE内积结果成反比，真很好的反映了token的相对位置关系。
就简单介绍到这里，关注不迷路(*^▽^*)