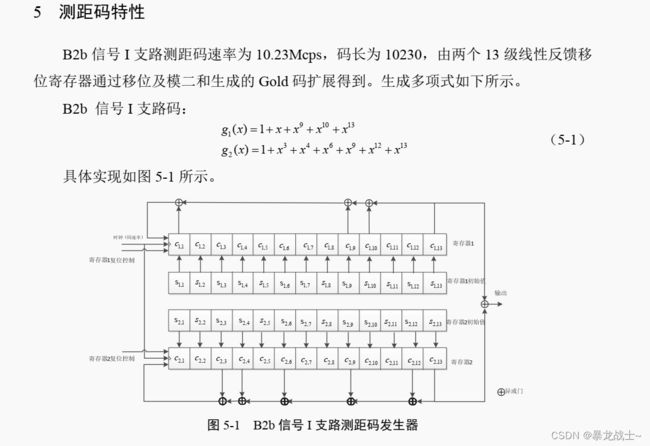
北斗卫星系统中几种常见编码的性能比较

1.1公开服务信号B2b（ 1.0版）

       gold序列由m序列优选对模2相加构成的，并且每改变一个m序列的相对位移，就可以得到一个新的Gold序列。这样每组m序列优选对可以产生2^r+1个Gold序列。b2b信号I的支路码为g1(x)和g2(x),所以我们可以先设计两组小m序列

%b2b的本原多项式
g1_poly=[1 0 0 0 0 0 0 0 1 1 0 0 1]; %去除最低位
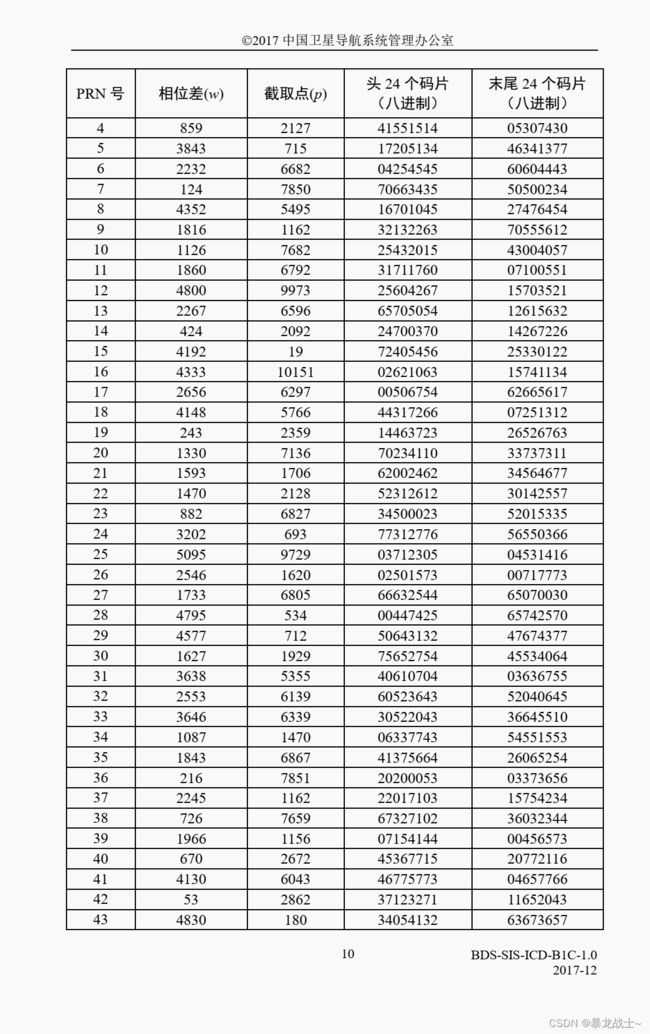
g2_poly=[0 0 1 1 0 1 0 0 1 0 0 1 1]; %去除最低位

 然后我们对寄存器1和寄存器2 进行初始化，寄存器1里面的值全部初始化为1 ，寄存器2排列方式由表5-1确定，码元长度太长我们可以做截断处理，只选取其中一部分按照所给定的操作进行排列即可

g1_innite=[1 1 1 1 1 1 1 1 1 1 1 1 1]; %g1寄存器的初始化
g2_innite=[ 1 0 0 0 1 1 0 1 0 1 1 1 0; %g2寄存器的初始化
            1 0 0 0 1 1 1 1 0 1 1 1 0;
            1 0 0 0 1 1 1 1 1 1 0 1 1;
            1 0 0 1 1 0 0 1 0 1 0 0 1;
            1 0 0 1 1 1 1 0 1 1 0 1 0;
            1 0 1 0 0 0 0 1 1 0 1 0 1;
            1 0 1 0 0 0 1 0 0 0 1 0 0;
           ];
       %码长N（通过截断）

N=10230;
%生成的两个m序列
g1=gen1(g1_poly,g1_innite,N);
g2=gen(g2_poly,g2_innite(prn,:),N);
%gold码为
g_b2b=mod(g1+g2,2);
g_b2b=2*g_b2b-1; %双极化操作

1.2公共服务信号B2c(1.0)版本

 

 

 

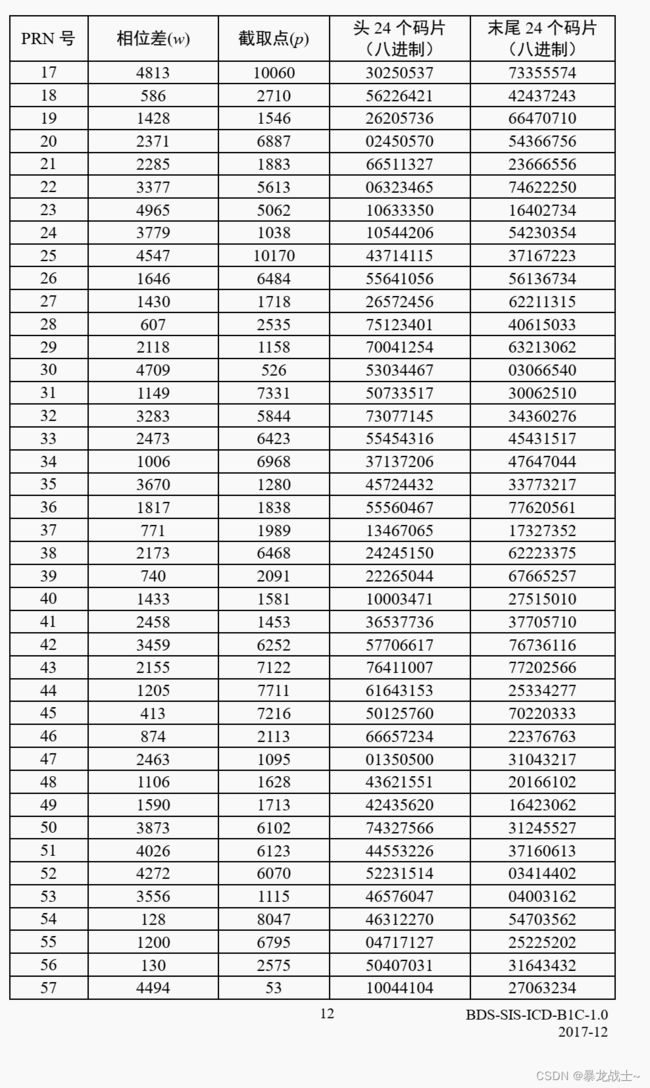
 先写出相位差和截断点

function [weil_b1c]=b1c_code(prn)
% B1C Data code
% Phase difference (w)
w=[2678 4802 958  859  3843 2232 124  4352 1816 1126 1860 4800 2267 424  4192 ...
   4333 2656 4148 243  1330 1593 1470 882  3202 5095 2546 1733 4795 4577 1627 ... 
   3638 2553 3646 1087 1843 216  2245 726  1966 670  4130 53   4830 182  2181 ...
   2006 1080 2288 2027 271  915  497  139  3693 2054 4342 3342 2592 1007 310 ...
   4203 455  4318];
% Truncation point (p) 
p=[699  694  7318 2127 715  6682 7850 5495 1162 7682 6792 9973 6596 2092 19 ...   
  10151 6297 5766 2359 7136 1706 2128 6827 693  9729 1620 6805 534  712  1929 ... 
   5355 6139 6339 1470 6867 7851 1162 7659 1156 2672 6043 2862 180  2663 6940 ... 
   1645 1582 951  6878 7701 1823 2391 2606 822  6403 239  442  6769 2560 2502 ... 
   5072 7268 341];

 2，

 我们根据Legendre序列的性质设计出代码

%产生类让得码（二次剩余是10243的一半）
L=zeros(1,10243);
for x=1:5121
    L(1+mod(x*x,10243))=1;
end

 生成weil序列

weil_b1c=zeros(1,10230);%初始化全为0 
for n=0:10229
    k=mod(n+p(prn)-1,10243);
    k_w=mod(k+w(prn),10243);
    weil_b1c(n+1)=mod(L(k+1)+L(k_w+1),2);
end

% Convert , 0 to -1
weil_b1c=2*weil_b1c-1; %双极化转换
end

 1.3空间接口信号控制B11文件

 

我们先设计g1(x)和g2(x)的本源多项式好的系数表达式，先把本源多项式的最低位去掉

function [g_b1i]=B1I_code(prn)
%g2的1本原多项式
%             
g1_poly=[1 0 0 0 0 0 1 1 1 1 1];
g2_poly=[1 1 1 1 1 0 0 1 1 0 1];
         
     
 %初始相位
g1_innite=[0 1 0 1 0 1 0 1 0 1 0];
g2_innite=[0 1 0 1 0 1 0 1 0 1 0];
%周期N截断最后一位；
N=2046;
%%%生成的两个m序列
 
g1=gen(g1_poly,g1_innite,N);
g2=gen(g2_poly(prn,:),g2_innite,N);



%gold码为
g_b1i=mod(g1+g2,2);
g_b1i=2*g_b1i-1;%进行双极化操作

B1i 和 B2b 的 gold码都设计好了，两者不同的地方一个是触发器所用的级数不同，一个是初始相位不同，与此同时，B2C 采用的是另外一种的编码方式，weil码的编码方式，我通过设计不同的函数接口，设计出自相关函数与互相关函数。

2.1m序列函数生成接口

function [m]=gen1(poly,inite,N) %m序列生成函数
len=length(inite); %初始化码片长度

m=zeros(1,N); %m序列初始化化置数成0
reg=inite;  
for i=1:N
    m(i)=reg(len);
    feedback=mod(sum(poly.*reg),2);
    reg(2:len)=reg(1:len-1); %移位
    reg(1)=feedback; %反馈到第一个触发器
    if(i==8190)   
        reg=[1 1 1 1 1 1 1 1 1 1 1 1 1];
    end    
end

2.2inter_dependent互相关，自相关函数接口函数

function inter_dependent(m1,m2)
period=length(m1);
m_1=[m1 m1 m1 m1 m1];
m_2=[m2 m2 m2 m2 m2];

for i=1:4*period
    
m3(i)=sum(m_1(1+i:period+i).*m_2(1:period))/period;
m4(i)=sum(m_1(1+i:period+i).*m_1(1:period))/period;
end

figure();
subplot(2,1,1);
plot(m3);
xlabel('x');
ylabel('y');
title('interdependent');


subplot(2,1,2);
plot(m4);
xlabel('x');
ylabel('y');
title('autodependent');

2.3各种编码方式的性能函数调用，比较自相关特性和互相关特性

b1i_1=B1I_code(1);
b1i_2=B1I_code(2);

inter_dependent(b1i_1,b1i_2) %b1i中gold码的互相关，与自相关比较

b2b_1=B2b_code(1);
b2b_2=B2b_code(2);
inter_dependent(b2b_1,b2b_2); %b2b中gold码的互相关，和自相关比较
b1c_1=b1c_code(1);
b1c_2=b1c_code(2);
inter_dependent(b1c_1,b1c_2); %b1c中weil码的互相关，和自相关比较

3.1仿真结果图b11_gold码

 从仿真结果图中可以看出互相关出现的峰值最大值为y =0.05767 ,自相关的最大旁瓣为 y = 0 .05963;

3.2 仿真结果图b2b_gold码

 b2b_gold码，互相关出现的峰值的最大值为 y = 0.1994 ,..自相关的最大旁瓣为0.03304。

3.3仿真结果图b1c_weil码的仿真图

 b1c_weil码，互相关出现的峰值的最大值为0.03812，自相关出现的最大旁瓣值为0.02561 ；

4.1总结

weil码的编码方法，相对于gold码的编码方式更为优秀，互相关特性和自相关特性都要好，但是设计方面更为复杂，程序设计更为复杂，gold码虽然并没有weil码的性能那么好，也就差一点点，但是也具有较好的自相关和互相关特性，编码方式更为简单。