基于动物迁徙优化算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、动物迁徙优化算法
- 2、AMO算法伪代码
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
1、动物迁徙优化算法
动物迁徙优化(Animal Migration Optimization, AMO)算法是李祥涛等于2013年提出的一种用于求解函数优化问题的新型群智能优化算法。AMO算法突出优点是可调节的参数少,算法实现简单且精度相对较高。同时,AMO有较强的广度和深度全局搜索能力,一般不会陷入局部最优,这使得AMO具有广阔的应用前景。
动物迁徙优化算法是模拟上述动物行为的优化算法,动物迁徙算法主要分为种群迁徙过程和个体更新过程。为了便于描述动物迁徙优化算法,首先做以下2个理想假设:
- 动物种群所处栖息地最优的动物个体将会保存到下一代。
- 动物种群在迁徙过程中,有的动物会离开种群,同时有新的动物个体会加入种群,假设动物种群的规模是确定的,动物会依概率 P a P_a Pa被新的个体所替代。
在迁徙过程中,算法模拟动物群体从当前所处栖息地域迂往新的所处栖息地域。在这个过程中,每个个体应当服从以上2个准则。在更新过程中,一些动物离开动物群体,一些动物又加入到动物群体。假定有一个全局最优解和候选的个体,置 D D D维空间编码向量表示一个个体,用最大值和最小值约束 D D D维向量;初始化种群大小为 N P NP NP,动物个体可表示为: X → min = { x 1 , min , x 2 , min , ⋯ , x D , min } (1) \overrightarrow X_{\min}=\left\{x_{1,\min},x_{2,\min},\cdots,x_{D,\min}\right\}\tag{1} Xmin={x1,min,x2,min,⋯,xD,min}(1) X → max = { x 1 , max , x 2 , max , ⋯ , x D , max } (2) \overrightarrow X_{\max}=\left\{x_{1,\max},x_{2,\max},\cdots,x_{D,\max}\right\}\tag{2} Xmax={x1,max,x2,max,⋯,xD,max}(2)因此,第 i i i个向量的第 j j j个分量初始化为: x j , i , 0 = x j , min + rand i , j [ 0 , 1 ] ⋅ ( x j , max − x j , min ) (3) x_{j,i,0}=x_{j,\min}+\text{rand}_{i,j}[0,1]\cdot(x_{j,\max}-x_{j,\min})\tag{3} xj,i,0=xj,min+randi,j[0,1]⋅(xj,max−xj,min)(3)其中, rand i , j [ 0 , 1 ] \text{rand}_{i,j}[0,1] randi,j[0,1]是在0和1之间服从均匀分布的随机数, i = 1 , 2 , ⋯ , N P i=1,2,\cdots,NP i=1,2,⋯,NP, j = 1 , 2 , ⋯ , D j=1,2,\cdots,D j=1,2,⋯,D。
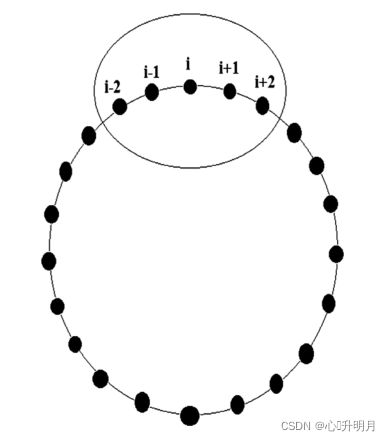
在动物迁徙过程中,动物会迁往食物丰富、水源充足、气候条件适宜的区域,此栖息地域可根据最优个体的位置确定最适宜动物所处栖息地域。动物个体服从3个准则:(1)个体和它邻居的位置不会冲突;(2)个体和邻居朝着相同的方向进斤迁徙;(3)新的个体仍然和原邻居相邻。对于第一条准则,要求群体中每个个体的位置不同。对于后两个准则,要求个体应当根据它邻居的当前位置迁往一个新的位置。图1采用一个环状拓扑结构解释个体邻居的定义。为了便于说明,设置每一维设置邻居的个数为5。如果个体的下标是 i i i,那么它的邻居下标是由下标为 i − 2 , i − 1 , i , i + 1 , i + 2 i-2,i-1,i,i+1,i+2 i−2,i−1,i,i+1,i+2组成。如果个体的下标是 1 1 1,那么它的邻居下标是由下标为 N P − 1 , N P , 1 , 2 , 3 NP-1,NP,1,2,3 NP−1,NP,1,2,3组成。如果个体的下标是 2 2 2,那么它的邻居下标是由下标为 N P , 1 , 2 , 3 , 4 NP,1,2,3,4 NP,1,2,3,4组成。如果个体的下标是 N P NP NP,那么它的邻居下标是由下标为 N P − 2 , N P − 1 , N P , 1 , 2 NP-2,NP-1,NP,1,2 NP−2,NP−1,NP,1,2组成。如果个体的下标是 N P − 1 NP-1 NP−1,那么它的邻居下标是由下标为 N P − 3 , N P − 2 , N P − 1 , N P , 1 NP-3,NP-2,NP-1,NP,1 NP−3,NP−2,NP−1,NP,1组成。邻居的拓扑结构建立之后,随机选择一个邻居,然后根据它邻居的位置更新个体的位置,更新公式如下: X i , G + 1 = X i , G + δ ⋅ ( X neighboorhood , G − X i , G ) (4) X_{i,G+1}=X_{i,G}+\delta\cdot(X_{\text{neighboorhood},G}-X_{i,G})\tag{4} Xi,G+1=Xi,G+δ⋅(Xneighboorhood,G−Xi,G)(4)其中, X neighboorhood , G X_{\text{neighboorhood},G} Xneighboorhood,G是邻居的当前位置;根据不同的问题可以改变 δ \delta δ的值,本文的 δ \delta δ是由高斯分布生成的随机数; X i , G X_{i,G} Xi,G是第 i i i个个体的位置; X i , G + 1 X_{i,G+1} Xi,G+1是第 i i i个个体的新位置。
在动物种群个体更新过程中,一些个体离开群体,同时一些个体又加入到群体中,假定群体的数量是恒定的,旧的个体会被新的个体按照概率 P a P_a Pa所取代。通过个体的适应度值来设置 P a P_a Pa,对于最好的适应度值, P a P_a Pa为1,对于最差的适应度值, P a P_a Pa为1/NP。该过程实施步骤如下:
 其中, r 1 , r 2 ∈ [ 1 , N P ] r_1,r_2\in[1,NP] r1,r2∈[1,NP]随机选取的整数,且 r 1 ≠ r 2 ≠ i r_1\neq r_2\neq i r1=r2=i。当产生新的后代解 X i , G + 1 X_{i,G+1} Xi,G+1后,会对 X i , G X_{i,G} Xi,G和 X i , G + 1 X_{i,G+1} Xi,G+1的适应度进行比较,如果新解更优才被保存至下一代。
其中, r 1 , r 2 ∈ [ 1 , N P ] r_1,r_2\in[1,NP] r1,r2∈[1,NP]随机选取的整数,且 r 1 ≠ r 2 ≠ i r_1\neq r_2\neq i r1=r2=i。当产生新的后代解 X i , G + 1 X_{i,G+1} Xi,G+1后,会对 X i , G X_{i,G} Xi,G和 X i , G + 1 X_{i,G+1} Xi,G+1的适应度进行比较,如果新解更优才被保存至下一代。
随着时间的推移,动物的生存区域内食物量不断减少,当食物耗尽时,动物耍迁出原栖息区域,即进行新一轮的迁徙,这样就完成了动物迁徙的过程。
2、AMO算法伪代码
二、仿真实验与分析
将AMO与PSO、DE、CS、GSA和ABC进行对比,实验设置种群规模为50,最大迭代次数为1500,每个算法独立运行25次,以常用23个测试函数中的F1、F2(单峰函数/30维)、F10、F11(多峰函数/30维)、F18、F19(固定维度多峰函数/2维、3维)为例,结果显示如下:




函数:F1
PSO:最差值: 149.6465, 最优值: 24.171, 平均值: 74.1763, 标准差: 36.5306, 秩和检验: 1.4157e-09
DE:最差值: 1.7842e-15, 最优值: 7.6355e-17, 平均值: 4.5412e-16, 标准差: 4.2518e-16, 秩和检验: 1.4157e-09
CS:最差值: 1.4179e-05, 最优值: 2.7967e-06, 平均值: 5.5278e-06, 标准差: 2.4281e-06, 秩和检验: 1.4157e-09
GSA:最差值: 3.0655e-17, 最优值: 1.0815e-17, 平均值: 1.7966e-17, 标准差: 4.4299e-18, 秩和检验: 1.4157e-09
ABC:最差值: 3.6496e-08, 最优值: 4.3648e-09, 平均值: 1.352e-08, 标准差: 6.9537e-09, 秩和检验: 1.4157e-09
AMO:最差值: 1.4194e-48, 最优值: 3.7815e-50, 平均值: 3.3755e-49, 标准差: 3.4229e-49, 秩和检验: 1
函数:F2
PSO:最差值: 7.0552, 最优值: 2.0069, 平均值: 4.3942, 标准差: 1.5362, 秩和检验: 1.4157e-09
DE:最差值: 1.5849e-07, 最优值: 1.0658e-08, 平均值: 6.0266e-08, 标准差: 3.8856e-08, 秩和检验: 1.4157e-09
CS:最差值: 0.13762, 最优值: 0.021838, 平均值: 0.058907, 标准差: 0.031631, 秩和检验: 1.4157e-09
GSA:最差值: 2.7006e-08, 最优值: 1.2876e-08, 平均值: 2.1022e-08, 标准差: 3.6661e-09, 秩和检验: 1.4157e-09
ABC:最差值: 7.7496e-08, 最优值: 2.3459e-08, 平均值: 4.782e-08, 标准差: 1.5489e-08, 秩和检验: 1.4157e-09
AMO:最差值: 1.7473e-26, 最优值: 2.3689e-27, 平均值: 9.021e-27, 标准差: 3.6268e-27, 秩和检验: 1
函数:F10
PSO:最差值: 8.7501, 最优值: 4.1375, 平均值: 6.127, 标准差: 0.99632, 秩和检验: 9.7285e-11
DE:最差值: 1.2229e-08, 最优值: 2.6363e-09, 平均值: 5.8608e-09, 标准差: 2.5608e-09, 秩和检验: 9.7285e-11
CS:最差值: 6.2232, 最优值: 0.24773, 平均值: 2.308, 标准差: 1.2014, 秩和检验: 9.7285e-11
GSA:最差值: 3.9279e-09, 最优值: 2.3455e-09, 平均值: 3.2144e-09, 标准差: 4.2036e-10, 秩和检验: 9.7285e-11
ABC:最差值: 5.3041e-05, 最优值: 1.9564e-05, 平均值: 3.4627e-05, 标准差: 8.9912e-06, 秩和检验: 9.7285e-11
AMO:最差值: 4.4409e-15, 最优值: 4.4409e-15, 平均值: 4.4409e-15, 标准差: 0, 秩和检验: NaN
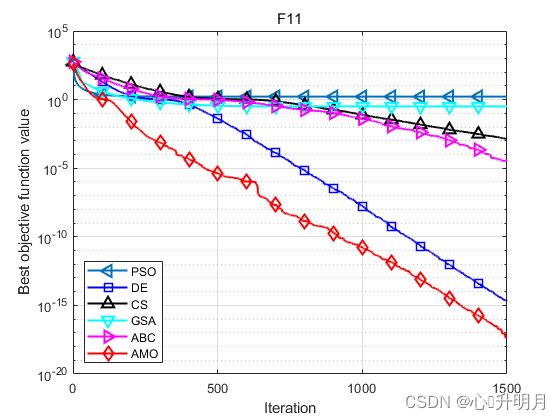
函数:F11
PSO:最差值: 2.4037, 最优值: 1.2683, 平均值: 1.6339, 标准差: 0.31542, 秩和检验: 1.3762e-10
DE:最差值: 3.8747e-14, 最优值: 0, 平均值: 2.0384e-15, 标准差: 7.6713e-15, 秩和检验: 3.8012e-07
CS:最差值: 0.0052815, 最优值: 9.7176e-05, 平均值: 0.0013631, 标准差: 0.0012985, 秩和检验: 1.3762e-10
GSA:最差值: 1.2262, 最优值: 0, 平均值: 0.31909, 标准差: 0.43684, 秩和检验: 2.7661e-08
ABC:最差值: 0.00080241, 最优值: 1.3309e-07, 平均值: 3.3862e-05, 标准差: 0.00016014, 秩和检验: 1.3762e-10
AMO:最差值: 1.1102e-16, 最优值: 0, 平均值: 4.4409e-18, 标准差: 2.2204e-17, 秩和检验: 1
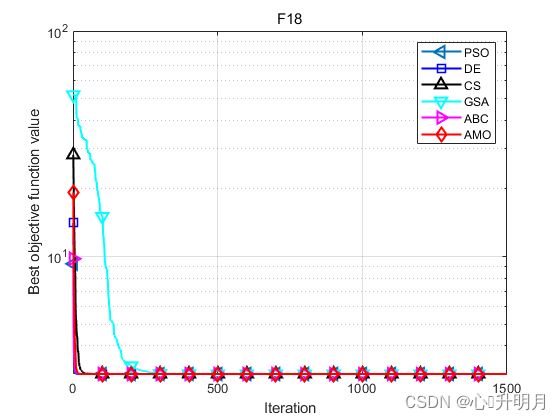
函数:F18
PSO:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.2979e-15, 秩和检验: 0.17351
DE:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.3597e-15, 秩和检验: 0.13047
CS:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 7.3644e-16, 秩和检验: 0.17095
GSA:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.7507e-15, 秩和检验: 1.2715e-07
ABC:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 3.0647e-15, 秩和检验: 1.8763e-09
AMO:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 1.0094e-15, 秩和检验: 1
函数:F19
PSO:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.2662e-15, 秩和检验: NaN
DE:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.2662e-15, 秩和检验: NaN
CS:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.2662e-15, 秩和检验: NaN
GSA:最差值: -2.8367, 最优值: -3.8628, 平均值: -3.4245, 标准差: 0.25433, 秩和检验: 3.6574e-10
ABC:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.2662e-15, 秩和检验: NaN
AMO:最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.2662e-15, 秩和检验: NaN
实验结果表明:AMO算法优于对比算法。
三、参考文献
[1] Li, X., Zhang, J., Yin, M. Animal migration optimization: an optimization algorithm inspired by animal migration behavior[J]. Neural Computing and Applications, 2014, 24: 1867-1877.
[2] 马明智. 动物迁徙算法及其应用研究[D]. 南宁: 广西民族大学, 2015.
