代码随想录算法训练营第二天|977.有序数组的平方 ,209.长度最小的子数组 ,59.螺旋矩阵II ,总结
977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10] 输出:[0,1,9,16,100] 解释:平方后,数组变为 [16,1,0,9,100] 排序后,数组变为 [0,1,9,16,100]
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums已按 非递减顺序 排序
进阶:
- 请你设计时间复杂度为
O(n)的算法解决本问题
排序问题,想到之前数据结构课学的一些排序方法:
O(n^2): Bubble sort, Selection sort, Insertion sort
O(nlogn): Mergesort, Quicksort, Heapsort
O(n): indexsort, bucketsort, countingsort
下图源自网络
个人对Shell Sort不太熟悉所以这里整理了一下:
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
因为没写过希尔排序所以这道题试着用了
class Solution {
public:
vector sortedSquares(vector& nums) {
for(int i=0;i0;gap/=2){
for(int i=gap;i=gap&&tmp 调用sort函数,时间复杂度为O(nlogn)
sort(nums.begin(), nums.end());
本题进阶要求时间复杂度O(n),使用双指针排序比较合
还是看了思路才写出来的
class Solution {
public:
vector sortedSquares(vector& nums) {
int k=nums.size()-1;
vector res(nums.size(),0);
int i=0;
int j=nums.size()-1;
while(i<=j){
if(nums[i]*nums[i] 时间复杂度降为O(n)
209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4] 输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1] 输出:0
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
进阶:
- 如果你已经实现
O(n)时间复杂度的解法, 请尝试设计一个O(n log(n))时间复杂度的解法。
滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
看了讲解之后才写出的代码
class Solution {
public:
int minSubArrayLen(int target, vector& nums) {
int j=0;
int sum=0;
int sublen=0;
int res=INT32_MAX;
for(int i=0;i=target){
sublen=i-j+1;
res=res - 时间复杂度:O(n)
- 空间复杂度:O(1)
不要以为for里放一个while就以为是O(n^2)啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)。
相关题目推荐
- 904.水果成篮(opens new window)
- 76.最小覆盖子串(opens new window)
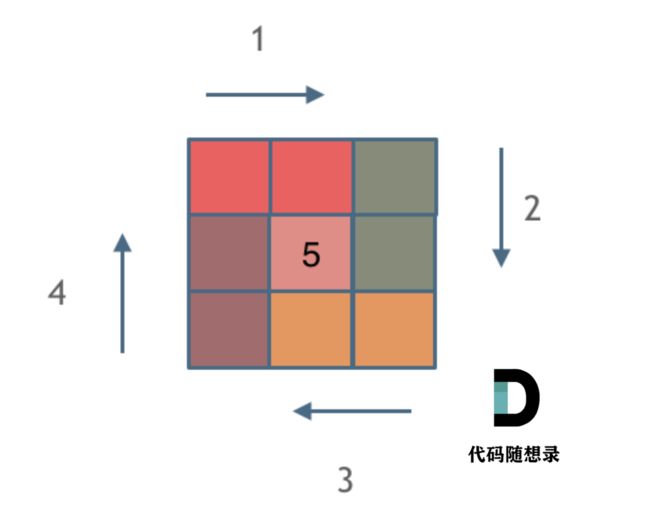
59. 螺旋矩阵 II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 20
一开始还是想不出做法
看了代码随想录的解析:
模拟类的题目在数组中很常见,不涉及到什么算法,就是单纯的模拟,考察对代码的掌控能力。
在这道题目中,我们再一次介绍到了循环不变量原则,其实这也是写程序中的重要原则。
时间复杂度O(n^2): 模拟遍历二维矩阵的时间
空间复杂度O(1)
class Solution {
public:
vector> generateMatrix(int n) {
vector> res(n,vector(n,0));
int loop=n/2;
int startx=0;
int starty=0;
int offset=1;
int count=1;
int i,j;
while(loop--){
i=startx;
j=starty;
for(j=starty;jstarty;j--){
res[i][j]=count++;
}
for(;i>startx;i--){
res[i][j]=count++;
}
startx++;
starty++;
offset++;
}
if(n%2){
res[n/2][n/2]=n*n;
}
return res;
}
}; 类似题目
- 54.螺旋矩阵(opens new window)
- 剑指Offer 29.顺时针打印矩阵
总结就copy随想录的一个思维导图啦(有空自己再整一个)
![]()