【时间序列论文】使用深度学习进行时间序列预测:一项调查
使用深度学习进行时间序列预测:一项调查
已经开发了许多深度学习架构来适应跨不同领域的时间序列数据集的多样性。在本文中,我们调查了单步和多水平时间序列预测中使用的常见编码器和解码器设计——描述了每个模型如何将时间信息纳入预测。接下来,我们重点介绍混合深度学习模型的最新发展,该模型将经过充分研究的统计模型与神经网络组件相结合,以改进任一类别的纯方法。最后,我们概述了深度学习还可以通过时间序列数据促进决策支持的一些方式。
1.简介
时间序列建模历来是学术研究的一个关键领域——形成了气候建模 [1]、生物科学 [2] 和医学 [3] 等主题应用的一个组成部分,以及商业决策制定零售 [4] 和金融 [5] 等等。虽然传统方法侧重于由领域专业知识提供信息的参数模型,例如自回归 (AR) [6]、指数平滑 [7、8] 或结构时间序列模型 [9],但现代机器学习方法提供了一种学习时间动态的方法以纯粹的数据驱动方式 [10]。随着近年来数据可用性和计算能力的提高,机器学习已成为下一代时间序列预测模型的重要组成部分。受图像分类 [11]、自然语言处理 [12] 和强化学习 [13] 方面的显着成就的启发,深度学习近年来尤其受到欢迎。通过结合反映底层数据集细微差别的定制架构假设(或归纳偏差 [14]),深度神经网络能够学习复杂的数据表示 [15],从而减轻了对手动特征工程和模型设计的需求。开源反向传播框架 [16、17] 的可用性也简化了网络训练,允许对网络组件和损失函数进行自定义。
鉴于跨各个领域的时间序列问题的多样性,出现了许多神经网络设计选择。在本文中,我们总结了使用深度神经网络进行时间序列预测的常用方法。首先,我们描述了可用于常见预测问题的最先进技术——例如多水平预测和不确定性估计。其次,我们分析了混合模型新趋势的出现,它将特定领域的定量模型与深度学习组件相结合,以提高预测性能。接下来,我们概述了神经网络可用于促进决策支持的两种关键方法,特别是通过可解释性和反事实预测中的方法。最后,我们总结了深度学习在时间序列预测方面的一些有前途的未来研究方向——特别是连续时间和层次模型的形式。虽然我们努力全面概述深度学习中的现代方法,但我们注意到我们的调查绝不是包罗万象的。事实上,关于时间序列预测的自动化方法存在丰富的文献——包括自动参数模型选择 [18],以及传统的机器学习方法,如内核回归 [19] 和支持向量回归 [20]。此外,高斯过程 [21] 已广泛用于时间序列预测——最近的扩展包括深度高斯过程 [22],以及通过神经过程进行深度学习的并行处理 [23]。此外,如 [24] 和 [25] 中所示,历史上曾在时间序列应用程序中使用过旧的神经网络模型。
2. 时间序列预测的深度学习架构
时间序列预测模型预测给定实体 i 在时间 t 的目标 y i , t y_{i,t} yi,t 的未来值。每个实体代表时间信息的逻辑分组——例如气候学中各个气象站的测量值,或医学中不同患者的生命体征——并且可以同时观察。在最简单的情况下,超前一步预测模型采用以下形式:
y ^ i , t + 1 = f ( y i , t − k : t , x i , t − k : t , s i ) 其 中 y ^ i , t + 1 是 模 型 预 测 , y i , t − k : t = { y i , t − k , . . . , u i , t } , x i , t − k : t = { x i , t − k , . . . , x i , t } 分 别 是 在 回 溯 窗 口 k 上 对 目 标 和 外 源 输 入 的 观 察 , s i 是 与 实 体 相 关 联 的 静 态 元 数 据 ( 例 如 传 感 器 位 置 ) , f ( : ) 是 模 型 学 习 的 预 测 函 数 。 虽 然 我 们 在 本 次 调 查 中 关 注 单 变 量 预 测 ( 即 一 维 目 标 ) , 但 我 们 注 意 到 相 同 的 组 件 可 以 扩 展 到 多 变 量 模 型 而 不 失 一 般 性 [ 26 、 27 、 28 、 29 、 30 ] 。 为 了 符 号 简 单 起 见 , 除 非 明 确 要 求 , 否 则 我 们 在 后 续 部 分 中 省 略 了 实 体 索 引 i 。 \hat y_{i,t+1}=f(y_{i,t-k:t},x_{i,t-k:t},s_i)\\ 其中 \hat y_{i,t+1}是模型预测,\\ y_{i,t-k:t}=\{y_{i,t-k},...,u_{i,t}\},x_{i,t-k:t}=\{x_{i,t-k},...,x_{i,t}\} \\分别是在回溯窗口 k 上对目标和外源输入的观察,\\ s_i 是与实体相关联的静态元数据(例如传感器位置),\\ f(:) 是模型学习的预测函数。\\虽然我们在本次调查中关注单变量预测(即一维目标),\\但我们注意到相同的组件可以扩展到多变量模型而不失一般性 [26、27、28、29、30]。\\为了符号简单起见,除非明确要求,否则我们在后续部分中省略了实体索引 i。 y^i,t+1=f(yi,t−k:t,xi,t−k:t,si)其中y^i,t+1是模型预测,yi,t−k:t={yi,t−k,...,ui,t},xi,t−k:t={xi,t−k,...,xi,t}分别是在回溯窗口k上对目标和外源输入的观察,si是与实体相关联的静态元数据(例如传感器位置),f(:)是模型学习的预测函数。虽然我们在本次调查中关注单变量预测(即一维目标),但我们注意到相同的组件可以扩展到多变量模型而不失一般性[26、27、28、29、30]。为了符号简单起见,除非明确要求,否则我们在后续部分中省略了实体索引i。
(a) 基本构建块
- 深度神经网络通过使用一系列非线性层来构建中间特征表示来学习预测关系 [15]。在时间序列设置中,这可以看作是将相关历史信息编码到潜在变量 z t z_t zt 中,最终预测仅使用 z t z_t zt 产生:
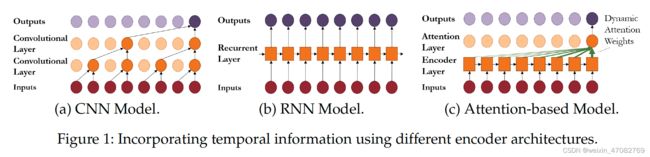
f ( y t − k L t , x t − k : t , s ) = g d e c ( z t ) z t = g e n c ( y t − k L t , x t − k : t , s ) 其 中 g e n c ( : ) 、 g d e c ( : ) 分 别 是 编 码 器 和 解 码 器 函 数 , 并 且 回 想 一 下 方 程 式 ( 2.1 ) 中 的 下 标 i 已 被 删 除 以 简 化 符 号 ( 例 如 y i , t 替 换 为 y t ) 。 因 此 , 这 些 编 码 器 和 解 码 器 构 成 了 深 度 学 习 架 构 的 基 本 构 建 块 , 网 络 的 选 择 决 定 了 我 们 的 模 型 可 以 学 习 的 关 系 类 型 。 在 本 节 中 , 我 们 将 研 究 编 码 器 的 现 代 设 计 选 择 ( 如 图 1 所 示 ) , 以 及 它 们 与 传 统 时 间 模 型 的 关 系 。 此 外 , 我 们 探 索 了 时 间 序 列 预 测 应 用 程 序 中 使 用 的 常 见 网 络 输 出 和 损 失 函 数 。 f(y_{t-kLt},x_{t-k:t},s)=g_{dec}(z_t) \\ z_t=g_{enc}(y_{t-kLt},x_{t-k:t},s) \\ 其中 genc(:)、gdec(:) 分别是编码器和解码器函数,\\ 并且回想一下方程式 (2.1) 中的下标 i 已被删除以简化符号(例如 y_{i,t} 替换为 y_t)。\\ 因此,这些编码器和解码器构成了深度学习架构的基本构建块,网络的选择决定了我们的模型可以学习的关系类型。\\ 在本节中,我们将研究编码器的现代设计选择(如图 1 所示),以及它们与传统时间模型的关系。\\ 此外,我们探索了时间序列预测应用程序中使用的常见网络输出和损失函数。 f(yt−kLt,xt−k:t,s)=gdec(zt)zt=genc(yt−kLt,xt−k:t,s)其中genc(:)、gdec(:)分别是编码器和解码器函数,并且回想一下方程式(2.1)中的下标i已被删除以简化符号(例如yi,t替换为yt)。因此,这些编码器和解码器构成了深度学习架构的基本构建块,网络的选择决定了我们的模型可以学习的关系类型。在本节中,我们将研究编码器的现代设计选择(如图1所示),以及它们与传统时间模型的关系。此外,我们探索了时间序列预测应用程序中使用的常见网络输出和损失函数。
(i) 卷积神经网络
传统上为图像数据集设计的卷积神经网络 (CNN) 提取在空间维度上不变的局部关系 [11, 31]。为了使 CNN 适应时间序列数据集,研究人员利用多层因果卷积 [32、33、34]——即旨在确保仅将过去的信息用于预测的卷积滤波器。对于隐藏层 l 的中间特征,每个因果卷积滤波器采用以下形式:
h t l + 1 = A ( ( W ∗ h ) ( l , t ) ) ( W ∗ h ) ( l , t ) = ∑ τ = 0 k W ( l , τ ) h t − τ l 其 中 h t l ∈ R H i n 为 t 时 刻 l 层 的 中 间 状 态 , 为 卷 积 算 子 , W ( l , τ ) ∈ R H o u t ∗ H i n 为 l 层 的 固 定 滤 波 器 权 重 , A ( : ) 为 激 活 函 数 , 如 一 个 s i g m o i d 函 数 , 表 示 任 何 特 定 于 体 系 结 构 的 非 线 性 处 理 。 对 于 总 共 使 用 L 个 卷 积 层 的 C N N , 我 们 注 意 到 编 码 器 输 出 为 z t = h t L 。 h_t^{l+1}=A((W*h)(l,t))\\ (W*h)(l,t)=\sum_{τ=0}^kW(l,τ)h_{t-τ}^l\\ 其中h_t^{l}\in R^{H_in} 为t时刻l层的中间状态,为卷积算子,W(l,τ)\in R^{H_{out}*H_{in}}为l层的固定滤波器权重\\ ,A(:)为激活函数,如一个 sigmoid 函数,表示任何特定于体系结构的非线性处理。\\ 对于总共使用 L 个卷积层的 CNN,我们注意到编码器输出为 z_t =h^L_t。\\ htl+1=A((W∗h)(l,t))(W∗h)(l,t)=τ=0∑kW(l,τ)ht−τl其中htl∈RHin为t时刻l层的中间状态,为卷积算子,W(l,τ)∈RHout∗Hin为l层的固定滤波器权重,A(:)为激活函数,如一个sigmoid函数,表示任何特定于体系结构的非线性处理。对于总共使用L个卷积层的CNN,我们注意到编码器输出为zt=htL。
考虑到一维情况,我们可以看出等式 (2.5) 与数字信号处理中的有限脉冲响应 (FIR) 滤波器非常相似 [35]。\
这对 CNN 学习的时间关系产生了两个关键影响。首先,根据标准 CNN 的空间不变性假设,时态 CNN 假设关系是时不变的——在每个时间步和所有时间使用相同的滤波器权重集。此外,CNN 只能使用其定义的回溯窗口或感受野内的输入来进行预测。因此,需要仔细调整感受野大小 k 以确保模型可以利用所有相关的历史信息。值得注意的是,具有线性激活函数的单个因果 CNN 层相当于一个自回归 (AR) 模型。
扩张卷积
使用标准卷积层在长期依赖性显着的情况下在计算上可能具有挑战性,因为参数的数量直接与感受野的大小成比例。为了缓解这种情况,现代架构经常使用扩张的卷积层 [32, 33],它扩展了等式 (2.5) 如下:
( W ∗ h ) ( l , t , d l ) = ∑ τ = 0 [ k / d l ] W ( l , τ ) h t − d l τ l 其 中 [ ⋅ ] 是 f l o o r 算 子 , d l 是 特 定 于 层 的 扩 张 率 。 因 此 , 空 洞 卷 积 可 以 解 释 为 下 层 特 征 的 下 采 样 版 本 的 卷 积 — — 降 低 分 辨 率 以 合 并 来 自 遥 远 过 去 的 信 息 。 因 此 , 通 过 增 加 每 一 层 的 扩 张 率 , 扩 张 卷 积 可 以 逐 渐 聚 合 不 同 时 间 块 的 信 息 , 从 而 允 许 以 有 效 的 方 式 使 用 更 多 历 史 。 例 如 , 使 用 [ 32 ] 的 W a v e N e t 架 构 , 扩 张 率 以 2 的 幂 增 加 , 相 邻 时 间 块 聚 集 在 每 一 层 中 — — 允 许 在 第 l 层 使 用 2 l 个 时 间 步 长 , 如 图 1 a 所 示 。 (W*h)(l,t,d_l) = \sum_{τ=0}^{[k/d_l]}W(l,τ)h_{t-d_{lτ}}^l \\ 其中 [·] 是 floor 算子,d_l 是特定于层的扩张率。\\ 因此,空洞卷积可以解释为下层特征的下采样版本的卷积——降低分辨率以合并来自遥远过去的信息。\\ 因此,通过增加每一层的扩张率,扩张卷积可以逐渐聚合不同时间块的信息,从而允许以有效的方式使用更多历史。\\ 例如,使用 [32] 的 WaveNet 架构,扩张率以 2 的幂增加,\\ 相邻时间块聚集在每一层中——允许在第 l 层使用 2^l 个时间步长,如图 1a 所示。 (W∗h)(l,t,dl)=τ=0∑[k/dl]W(l,τ)ht−dlτl其中[⋅]是floor算子,dl是特定于层的扩张率。因此,空洞卷积可以解释为下层特征的下采样版本的卷积——降低分辨率以合并来自遥远过去的信息。因此,通过增加每一层的扩张率,扩张卷积可以逐渐聚合不同时间块的信息,从而允许以有效的方式使用更多历史。例如,使用[32]的WaveNet架构,扩张率以2的幂增加,相邻时间块聚集在每一层中——允许在第l层使用2l个时间步长,如图1a所示。
(ii) 递归神经网络
递归神经网络 (RNN) 历来被用于序列建模 [31],在各种自然语言处理任务中取得了很好的效果 [36]。考虑到时间序列数据作为输入和目标序列的自然解释,许多基于 RNN 的架构已被开发用于时间预测应用程序 [37、38、39、40]。在其核心,RNN 单元包含一个内部记忆状态,它充当过去信息的紧凑摘要。如图 1b 所示,在每个时间步用新观察值递归更新内存状态,即:
z t = v ( z t − 1 , y t , x t , s ) 其 中 z t ∈ R H 这 里 是 R N N 的 隐 藏 内 部 状 态 , v ( ⋅ ) 是 学 习 到 的 记 忆 更 新 函 数 。 例 如 , E l m a n R N N [ 41 ] , 最 简 单 的 R N N 变 体 之 一 , 将 采 用 以 下 形 式 : z_t = v(z_{t-1},y_t,x_t,s)\\ 其中z_t\in R^H这里是RNN的隐藏内部状态,v(·)是学习到的记忆更新函数。\\ 例如,Elman RNN [41],最简单的 RNN 变体之一,将采用以下形式: zt=v(zt−1,yt,xt,s)其中zt∈RH这里是RNN的隐藏内部状态,v(⋅)是学习到的记忆更新函数。例如,ElmanRNN[41],最简单的RNN变体之一,将采用以下形式:
y t + 1 = γ y ( W y z t + b y ) z t = γ z ( W z 1 z t − 1 + W z 2 y t + W z 3 x t + W z 4 s + b z ) 其 中 W ; b 分 别 是 网 络 的 线 性 权 重 和 偏 置 , γ y ( ⋅ ) ; γ z ( ⋅ ) 是 网 络 激 活 函 数 。 请 注 意 , R N N 不 需 要 像 C N N 案 例 那 样 明 确 指 定 回 溯 窗 口 。 从 信 号 处 理 的 角 度 来 看 , 主 要 的 循 环 层 — — 即 方 程 ( 2.9 ) — — 因 此 类 似 于 无 限 脉 冲 响 应 ( I I R ) 滤 波 器 的 非 线 性 版 本 y_{t+1}=γ_y(W_yz_t+b_y)\\ z_t = γ_z(W_{z_1}z_{t-1}+W_{z_2}y_t+W_{z_3}x_t+W_{z_4}s+b_z)\\ 其中 W; b分别是网络的线性权重和偏置,γ_y(·); γ_z(·) 是网络激活函数。\\ 请注意,RNN 不需要像 CNN 案例那样明确指定回溯窗口。\\ 从信号处理的角度来看,主要的循环层——即方程 (2.9)——因此类似于无限脉冲响应 (IIR) 滤波器的非线性版本 yt+1=γy(Wyzt+by)zt=γz(Wz1zt−1+Wz2yt+Wz3xt+Wz4s+bz)其中W;b分别是网络的线性权重和偏置,γy(⋅);γz(⋅)是网络激活函数。请注意,RNN不需要像CNN案例那样明确指定回溯窗口。从信号处理的角度来看,主要的循环层——即方程(2.9)——因此类似于无限脉冲响应(IIR)滤波器的非线性版本
长期短期记忆
由于无限的回溯窗口,RNN 的旧变体在学习数据中的长期依赖性方面可能会受到限制 [42、43] – 由于梯度爆炸和消失的问题 [31]。直观上,这可以看作是记忆状态中的一种共振形式。因此开发了长短期记忆网络 (LSTM) [44] 来解决这些限制,方法是改进网络内的梯度流。这是通过使用存储长期信息的单元状态 ct 实现的,通过以下一系列门进行调制:
I n p u t g a t e : i t = σ ( W i 1 z t − 1 + W i 2 y t + W i 3 x t + W i 4 s + b i ) O u t p u t g a t e : o t = σ ( W o 1 z t − 1 + W o 2 y t + W o 3 x t + W o 4 s + b o ) F o r g e t g a t e : f t = σ ( W f 1 z t − 1 + W f 2 y t + W f 3 x t + W f 4 s + b f ) 其 中 z t − 1 是 L S T M 的 隐 藏 状 态 , σ ( ⋅ ) 是 s i g m o i d 激 活 函 数 。 门 修 改 L S T M 的 隐 藏 状 态 和 单 元 状 态 , 如 下 所 示 : Input \ gate: i_t = \sigma(W_{i_1}z_{t-1}+W_{i_2}y_t+W_{i_3}x_t+W_{i_4}s+b_i)\\ Output\ gate:o_t = \sigma(W_{o_1}z_{t-1}+W_{o_2}y_t+W_{o_3}x_t+W_{o_4}s+b_o)\\ Forget \ gate:f_t = \sigma(W_{f_1}z_{t-1}+W_{f_2}y_t+W_{f_3}x_t+W_{f_4}s+b_f)\\ 其中 z_{t-1} 是 LSTM 的隐藏状态,\sigma(·) 是 sigmoid 激活函数。门修改 LSTM 的隐藏状态和单元状态,如下所示: Input gate:it=σ(Wi1zt−1+Wi2yt+Wi3xt+Wi4s+bi)Output gate:ot=σ(Wo1zt−1+Wo2yt+Wo3xt+Wo4s+bo)Forget gate:ft=σ(Wf1zt−1+Wf2yt+Wf3xt+Wf4s+bf)其中zt−1是LSTM的隐藏状态,σ(⋅)是sigmoid激活函数。门修改LSTM的隐藏状态和单元状态,如下所示:
H i d d e n s t a t e : z t = o t ⋅ t a n h ( c t ) C e l l s t a t e L c t = f t ⋅ c t − 1 + i t ⋅ t a n h ( σ ( W c 1 z t − 1 + W c 2 y t + W c 3 x t + W c 4 s + b c ) ) 其 中 ⋅ 是 逐 元 素 ( H a d a m a r d ) 乘 积 , t a n h ( d ⋅ ) 是 t a n h 激 活 函 数 。 Hidden\ state: z_t = o_t·tanh(c_t)\\ Cell \ stateL c_t = f_t·c_{t-1}+ i_t·tanh(\sigma(W_{c_1}z_{t-1}+W_{c_2}y_t+W_{c_3}x_t+W_{c_4}s+b_c))\\ 其中·是逐元素 (Hadamard) 乘积,tanh(d·) 是 tanh 激活函数。 Hidden state:zt=ot⋅tanh(ct)Cell stateLct=ft⋅ct−1+it⋅tanh(σ(Wc1zt−1+Wc2yt+Wc3xt+Wc4s+bc))其中⋅是逐元素(Hadamard)乘积,tanh(d⋅)是tanh激活函数。
与贝叶斯过滤的关系
正如 [39] 中所检查的那样,贝叶斯过滤器 [45] 和 RNN 在维护随时间递归更新的隐藏状态方面都很相似。对于贝叶斯滤波器,例如卡尔曼滤波器 [46],推理是通\过更新潜在状态的充分统计信息来执行的——使用一系列状态转换和纠错步骤。由于贝叶斯过滤步骤使用确定性方程来修改足够的统计数据,因此 RNN 可以看作是两个步骤的同时逼近——记忆向量包含预测所需的所有相关信息
(iii) 注意力机制
注意力机制 [47, 48] 的发展也导致了长期依赖学习的改进——Transformer 架构在多种自然语言处理应用程序中实现了最先进的性能 [12, 49, 50]。注意层使用动态生成的权重聚合时间特征(参见图 1c),使网络能够直接关注过去的重要时间步长——即使它们在回溯窗口中非常遥远。从概念上讲,注意力是一种基于给定查询 [51] 的键值查找机制,采用以下形式:
h t = ∑ τ = 0 k α ( k t , q τ ) v t − τ 其 中 键 k t 、 查 询 q τ 和 值 v t − τ 是 网 络 较 低 层 在 不 同 时 间 步 生 成 的 中 间 特 征 。 此 外 , α ( k t , q τ ) ∈ [ 0 ; 1 ] 是 在 时 间 t 生 成 的 t − τ 的 注 意 权 重 , h t 是 注 意 层 的 上 下 文 向 量 输 出 。 请 注 意 , 根 据 C N N 的 情 况 , 多 个 注 意 力 层 也 可 以 一 起 使 用 , 最 后 一 层 的 输 出 形 成 编 码 的 潜 在 变 量 z t 。 h_t = \sum_{τ=0}^k \alpha(k_t,q_τ)v_{t-τ}\\ 其中键 k_t、查询 q_τ 和值 v_{t-τ} 是网络较低层在不同时间步生成的中间特征。\\ 此外,\alpha(k_t,q_τ)\in [0; 1] 是在时间 t 生成的 t-τ 的注意权重,h_t 是注意层的上下文向量输出。\\ 请注意,根据 CNN 的情况,多个注意力层也可以一起使用,最后一层的输出形成编码的潜在变量 z_t。 ht=τ=0∑kα(kt,qτ)vt−τ其中键kt、查询qτ和值vt−τ是网络较低层在不同时间步生成的中间特征。此外,α(kt,qτ)∈[0;1]是在时间t生成的t−τ的注意权重,ht是注意层的上下文向量输出。请注意,根据CNN的情况,多个注意力层也可以一起使用,最后一层的输出形成编码的潜在变量zt。
α ( t ) = s o f t m a x ( η t ) η t = W η 1 t a n h ( W η 2 k t − 1 + W η 3 q τ + b η ) 其 中 α ( t ) = [ α ( t , 0 ) , . . . α ( t , k ) ] 是 注 意 力 权 重 的 向 量 , k t − 1 , q t 是 用 于 特 征 提 取 的 L S T M 编 码 器 的 输 出 , s o f t m a x ( : ) 是 s o f t m a x 激 活 函 数 。 \alpha(t)=softmax(\eta_t)\\ \eta_t = W_{\eta_1}tanh(W_{\eta2}k_{t-1}+W_{\eta3}q_τ+b_\eta)\\ 其中\alpha(t)=[\alpha(t,0),...\alpha(t,k)] 是注意力权重的向量,\\ k_{t-1},q_t是用于特征提取的 LSTM 编码器的输出,softmax(:) 是 softmax 激活函数。 α(t)=softmax(ηt)ηt=Wη1tanh(Wη2kt−1+Wη3qτ+bη)其中α(t)=[α(t,0),...α(t,k)]是注意力权重的向量,kt−1,qt是用于特征提取的LSTM编码器的输出,softmax(:)是softmax激活函数。
最近,[53、54] 中也考虑了 Transformer 架构,它将标量点积自注意力 [49] 应用于回溯窗口中提取的特征。从时间序列建模的角度来看,注意力提供了两个主要好处。首先,具有注意力的网络能够直接关注发生的任何重大事件。例如,在零售预测应用程序中,这包括可能对销售产生积极影响的假期或促销期。其次,如 [54] 所示,基于注意力的网络还可以通过为每个状态使用不同的注意力权重模式来学习特定于状态的时间动
(iv) 输出和损失函数
鉴于神经网络的灵活性,深度神经网络已被用于对离散 [55] 和连续 [37、56] 目标进行建模——通过定制神经网络的解码器和输出层以匹配所需的目标类型。在一步预测问题中,这可以简单到将编码器输出的线性变换(即等式(2.2))与目标的适当输出激活结合起来。无论目标的形式如何,预测都可以进一步分为两个不同的类别——点估计和概率预测。
点估计
一种常见的预测方法是确定未来目标的预期值。这基本上涉及将问题重新表述为离散输出的分类任务(例如预测未来事件)和连续输出的回归任务——使用上述编码器。对于二进制分类情况,解码器的最后一层具有一个带有 S 形激活函数的线性层——允许网络预测事件在给定时间步发生的概率。对于二进制和连续目标的一步预测,网络分别使用二进制交叉熵和均方误差损失函数进行训练:
L c l a s s i f i c a t i o n = − 1 T ∑ t = 1 T y t l o f ( y ^ t ) + ( 1 − y t ) l o g ( 1 − y ^ t ) L r e g r e s s i o n = 1 T ∑ t = 1 T ( y t − y ^ t ) 2 L_{classification} = -\frac{1}{T}\sum_{t=1}^Ty_tlof(\hat y_t)+(1-y_t)log(1-\hat y_t)\\ L_{regression} =\frac{1}{T}\sum_{t=1}^T(y_t-\hat y_t)^2\\ Lclassification=−T1t=1∑Tytlof(y^t)+(1−yt)log(1−y^t)Lregression=T1t=1∑T(yt−y^t)2
虽然上述损失函数在应用程序中最常见,但我们注意到神经网络的灵活性也允许采用更复杂的损失——例如分位数回归 [56] 和多项分类 [32] 的损失。
概率输出
虽然点估计对于预测目标的未来价值至关重要,但了解模型预测的不确定性对于不同领域的决策者可能很有用。例如,当预测的不确定性很大时,模型用户在将预测纳入决策时可以更加谨慎,或者依赖其他信息来源。在某些应用程序中,例如金融风险管理,获得完整的预测分布将使决策者能够在出现罕见事件时优化他们的行动——例如,允许风险管理者使投资组合免受市场崩溃的影响。对不确定性建模的一种常见方法是使用深度神经网络生成已知分布的参数 [27、37、38]。例如,高斯分布通常用于预测具有连续目标的问题,网络在每个步骤输出预测分布的均值和方差参数,如下所示
y t + τ N ( μ ( t , τ ) , ζ ( t , τ ) 2 ) μ ( t , τ ) = W μ h t L + b μ ζ ( t , τ ) = s o f t p l u s ( W ∑ h t L + b ∑ ) 其 中 h t L 是 网 络 的 最 后 一 层 , s o f t p l u s ( : ) 是 s o f t p l u s 激 活 函 数 , 以 确 保 标 准 差 只 取 正 值 。 y_{t+τ} ~ N(\mu(t,τ),\zeta(t,τ)^2)\\ \mu(t,τ) = W_\mu h_t^L+b_\mu\\ \zeta(t,τ)=softplus(W_{\sum} h_t^L+b_{\sum})\\ 其中 h^L_t 是网络的最后一层,softplus(:) 是 softplus 激活函数,以确保标准差只取正值。 yt+τ N(μ(t,τ),ζ(t,τ)2)μ(t,τ)=WμhtL+bμζ(t,τ)=softplus(W∑htL+b∑)其中htL是网络的最后一层,softplus(:)是softplus激活函数,以确保标准差只取正值。
(b) 多水平预测模型
在许多应用中,访问未来多个点的预测估计通常是有益的——允许决策者可视化未来水平的趋势,并优化他们在整个路径上的行动。从统计的角度来看,多水平预测可以看作是对一步预测问题(即方程(2.1))的轻微修改,如下所示:
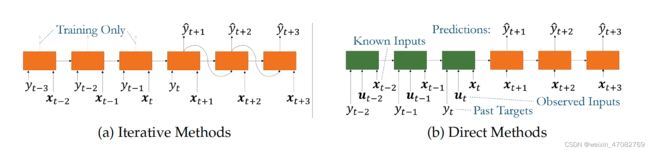
y ^ t + τ = f ( y t − k : t , x t − k : t , u t − k : t + τ , s , τ ) 其 中 τ ∈ { 1 , . . . , τ m a x } 是 一 个 离 散 的 预 测 范 围 , u t 是 整 个 范 围 内 已 知 的 未 来 输 入 ( 例 如 日 期 信 息 , 例 如 星 期 几 或 月 份 ) , x t 是 只 能 在 历 史 上 观 察 到 的 输 入 。 与 传 统 的 计 量 经 济 学 方 法 [ 57 、 58 ] 一 致 , 用 于 多 层 次 预 测 的 深 度 学 习 架 构 可 以 分 为 迭 代 法 和 直 接 法 — — 如 图 2 所 示 , 并 在 下 面 详 细 描 述 。 \hat y_{t+τ} = f(y_{t-k:t},x_{t-k:t},u_{t-k:t+τ},s,τ)\\ 其中τ\in \{1,...,τ_{max}\} 是一个离散的预测范围,u_t 是整个范围内已知的未来输入(例如日期信息,例如星期几或月份),\\ x_t 是只能在历史上观察到的输入。\\ 与传统的计量经济学方法 [57、58] 一致,用于多层次预测的深度学习架构可以分为迭代法和直接法——如图 2 所示,并在下面详细描述。 y^t+τ=f(yt−k:t,xt−k:t,ut−k:t+τ,s,τ)其中τ∈{1,...,τmax}是一个离散的预测范围,ut是整个范围内已知的未来输入(例如日期信息,例如星期几或月份),xt是只能在历史上观察到的输入。与传统的计量经济学方法[57、58]一致,用于多层次预测的深度学习架构可以分为迭代法和直接法——如图2所示,并在下面详细描述。
(i) 迭代方法
多水平预测的迭代方法通常利用自回归深度学习架构 [37、39、40、53]——通过将目标样本递归地馈送到未来的时间步长来产生多水平预测(见图 2a) ).通过重复生成多个轨迹的过程,然后使用每个步骤中目标值的抽样分布生成预测。例如,可以使用蒙特卡洛估计
y ^ t + τ = ∑ j = 1 J y ˉ t + τ ( j ) J 其 中 , \hat y_{t+τ}=\sum_{j=1}^J \frac{\bar y_{t+τ}^{(j)}}{J} 其中, y^t+τ=∑j=1JJyˉt+τ(j)其中, 获得预测均值,其中 y ˉ t + τ ( j ) \bar y_{t+τ}^{(j)} yˉt+τ(j)是基于方程 (2.20) 的模型获取的样本。由于自回归模型的训练方式与前一步预测模型完全相同
图 2:多水平预测模型的主要类型。用于区分模型权重的颜色——迭代模型在整个范围内使用通用模型,直接方法采用序列到序列的方法。
(即通过时间反向传播),因此迭代方法可以轻松地将标准模型推广到多步预测。然而,由于在每个时间步都会产生少量误差,迭代方法的递归结构可能会导致在更长的预测范围内产生大量误差累积。此外,迭代方法假设除了目标之外的所有输入在运行时都是已知的——只需要将目标样本输入到未来的时间步长中。在存在观察到的输入的许多实际场景中,这可能是一个限制,激发了对更灵活方法的需求。
(ii) 直接方法
直接方法通过使用所有可用输入直接生成预测来减轻迭代方法的问题。他们通常使用序列到序列架构 [52、54、56],使用编码器总结过去的信息(即目标、观察到的输入和先验已知输入),并使用解码器将它们与已知的未来输入结合起来——如图 2b 所示。如 [59] 中所述,替代方法是使用更简单的模型直接生成与所需预测范围匹配的固定长度向量。然而,这确实需要指定最大预测范围(即最大值),并且仅在预定义的离散间隔内进行预测。
3. 将领域知识与混合模型相结合
尽管它很受欢迎,但机器学习在时间序列预测中的功效历来受到质疑——正如 M-competitions [60] 等预测竞赛所证明的那样。在 2018 年的 M4 竞赛 [61] 之前,普遍的看法是复杂的方法不会产生更准确的预测,而带有集成的简单模型往往会做得更好 [59、62、63]。已经确定了两个关键原因来解释机器学习方法的性能不佳。首先,机器学习方法的灵活性可能是一把双刃剑——使它们容易过度拟合 [59]。因此,更简单的模型可能在低数据条件下表现更好,这在预测具有少量历史观察的问题(例如季度宏观经济预测)中尤为常见。其次,与统计模型的平稳性要求类似,机器学习模型可以对输入的预处理方式敏感 [26、37、59],从而确保训练和测试时的数据分布相似。深度学习的最新趋势是开发混合模型来解决这些限制,在各种应用程序中展示了比纯统计或机器学习模型更高的性能 [38、64、65、66]。混合方法将经过充分研究的定量时间序列模型与深度学习相结合——使用深度神经网络在每个时间步生成模型参数。一方面,混合模型允许领域专家使用先验信息为神经网络训练提供信息——减少网络的假设空间并提高泛化能力。这对于小型数据集特别有用 [38],其中深度学习模型过度拟合的风险更大。此外,混合模型允许分离固定和非固定组件,并避免自定义输入预处理的需要。这方面的一个例子是指数平滑 RNN (ES-RNN) [64],它是 M4 竞赛的获胜者,它使用指数平滑来捕捉非平稳趋势并通过 RNN 学习额外的效果。通常,混合模型以两种方式利用深度神经网络:a) 为非概率参数模型 [64、65、67] 编码时变参数,以及 b) 生成概率模型使用的分布参数 [38, 40, 66]。
(a) 非概率混合模型
对于参数时间序列模型,预测方程通常是分析定义的,并为未来目标提供点预测。因此,非概率混合模型修改这些预测方程以结合统计和深度学习组件。例如,ES-RNN 利用 Holt-Winters 指数平滑模型 [8] 的更新方程——将乘法水平和季节性成分与深度学习输出相结合,如下所示:
y ^ i , t + τ = e x p ( W E S h i , t + τ L + b E S ) ∗ L i , t ∗ y i , t + τ l i , t = β 1 ( i ) y i , t y i , t + ( 1 − β 1 ( i ) ) l i , t − 1 γ i , t = β 2 ( i ) l i , t + ( 1 − β 2 ( i ) γ i , t − K 其 中 , h i , t + τ L 是 第 τ 步 预 测 网 络 的 最 后 一 层 l i , t 是 水 平 分 量 , γ i , t 是 周 期 为 k 的 季 节 性 分 量 , 并 且 β 1 ( i ) , β 2 ( i ) 是 实 体 特 定 的 静 态 系 数 。 从 上 面 的 等 式 中 , 我 们 可 以 看 到 指 数 平 滑 分 量 ( l i , t , γ i , t ) 处 理 数 据 集 中 更 广 泛 的 ( 例 如 指 数 ) 趋 势 , 减 少 了 额 外 输 入 缩 放 的 需 要 。 \hat y_{i,t+τ}=exp(W_{ES}h_{i,t+τ}^L+b_{ES})*L_{i,t}*y_{i,t+τ}\\ l_{i,t}=\frac{β_1^{(i)}y_{i,t}}{y_{i,t}}+(1-\beta _1^{(i)})l_{i,t-1}\\ γ_{i,t}=\frac{\beta_2^{(i)}}{l_{i,t}}+(1-β_2^{(i)}γ_{i,t-K}\\ 其中, h_{i,t+τ}^L 是第 τ 步预测网络的最后一层\\ l_{i,t} 是水平分量,γ_{i,t} 是周期为k的季节性分量,\\ 并且β_1^{(i)}, β_2^{(i)}是实体特定的静态系数。\\ 从上面的等式中,我们可以看到指数平滑分量 (l_{i,t},γ_{i,t}) 处理数据集中更广泛的(例如指数)趋势,减少了额外输入缩放的需要。 y^i,t+τ=exp(WEShi,t+τL+bES)∗Li,t∗yi,t+τli,t=yi,tβ1(i)yi,t+(1−β1(i))li,t−1γi,t=li,tβ2(i)+(1−β2(i)γi,t−K其中,hi,t+τL是第τ步预测网络的最后一层li,t是水平分量,γi,t是周期为k的季节性分量,并且β1(i),β2(i)是实体特定的静态系数。从上面的等式中,我们可以看到指数平滑分量(li,t,γi,t)处理数据集中更广泛的(例如指数)趋势,减少了额外输入缩放的需要。
(b) 概率混合模型
概率混合模型也可用于分布建模很重要的应用程序——利用概率生成模型进行时间动态,例如高斯过程 [40] 和线性状态空间模型 [38]。概率混合模型不是修改预测方程,而是使用神经网络在每个步骤中为预测分布生成参数。例如,深度状态空间模型 [38] 对线性状态空间模型的时变参数进行编码,如下所示——通过卡尔曼滤波方程 [46] 执行推理:
y t = α ( h i , t + τ L ) T l t + φ ( ( h i , t + τ L ) ϵ t l t = F ( ( h i , t + τ L ) l t − 1 + q ( h i , t + τ L ) + ∑ ( h i , t + τ L ) ∗ ∑ t 其 中 l t 是 隐 藏 的 潜 在 状 态 , a ( ⋅ ) , F ( ⋅ ) , q ( ⋅ ) 是 h i , t + τ L 的 线 性 变 换 ; ϕ ( ⋅ ) , ∑ ( ⋅ ) 是 具 有 s o f t m a x 激 活 的 线 性 变 换 , ϵ t N ( 0 ; 1 ) 是 单 变 量 残 差 , ∑ t N ( 0 ; I ) 是 多 元 正 态 随 机 变 量 yt = \alpha(h_{i,t+τ}^L)^Tl_t+φ((h_{i,t+τ}^L)\epsilon_t\\ l_t = F((h_{i,t+τ}^L)l_{t-1}+q(h_{i,t+τ}^L)+\sum(h_{i,t+τ}^L)* \sum_t \\ 其中 l_t 是隐藏的潜在状态,a(·), F(·), q(·) 是h_{i,t+τ}^L的线性变换;\phi(·), \sum(·) 是具有 softmax 激活的线性变换,\\ \epsilon_t~N(0; 1) 是单变量残差,\sum_t~N(0; I) 是多元正态随机变量 yt=α(hi,t+τL)Tlt+φ((hi,t+τL)ϵtlt=F((hi,t+τL)lt−1+q(hi,t+τL)+∑(hi,t+τL)∗t∑其中lt是隐藏的潜在状态,a(⋅),F(⋅),q(⋅)是hi,t+τL的线性变换;ϕ(⋅),∑(⋅)是具有softmax激活的线性变换,ϵt N(0;1)是单变量残差,t∑ N(0;I)是多元正态随机变量
4. 使用深度神经网络促进决策支持
虽然模型构建者主要关心预测的准确性,但最终用户通常使用预测来指导他们未来的行动。例如,医生可以利用临床预测(例如疾病发作和死亡的概率)来帮助他们确定测试的优先顺序、制定诊断并确定治疗过程。因此,虽然时间序列预测是关键的初步步骤,但更好地理解时间动态和模型预测背后的动机可以帮助用户进一步优化他们的行动。在本节中,我们探索了神经网络扩展的两个方向,以促进时间序列数据的决策支持——重点是可解释性和因果推理的方法。
(a) 时间序列数据的可解释性
随着神经网络在任务关键型应用程序中的部署 [68],人们越来越需要了解模型如何以及为何做出某种预测。此外,随着近来数据集的规模和复杂性不断增加,最终用户对其数据中存在的关系几乎没有先验知识。鉴于标准神经网络架构的黑盒性质,在解释深度学习模型的方法方面出现了新的研究机构。我们在下面提供了一个摘要——请读者参考专门的调查以进行更深入的分析 [69、70]。
事后可解释性技术开发事后可解释模型来解释经过训练的网络,并帮助识别重要特征或示例,而无需修改原始权重。方法主要可以分为两大类。首先,一种可能的方法是在神经网络的输入和输出之间应用更简单的可解释代理模型,并依靠近似模型来提供解释。例如,局部可解释模型不可知论解释 (LIME) [71] 通过将特定于实例的线性模型拟合到输入的扰动来识别相关特征,线性系数提供重要性的度量。 Shapley 加性解释 (SHAP) [72] 提供了另一种替代方法,它利用合作博弈论中的 Shapley 值来识别数据集中的重要特征。接下来,提出了基于梯度的方法,例如显着图 [73、74] 和影响函数 [75],它们分析网络梯度以确定哪些输入特征对损失函数的影响最大。虽然事后可解释性方法可以帮助进行特征归因,但它们通常会忽略输入之间的任何顺序依赖性——这使得它们很难应用于复杂的时间序列数据集。
AttentionWeights 的固有可解释性另一种方法是直接设计具有可解释组件的体系结构,通常以战略性放置注意力层的形式出现。由于注意力权重是作为 softmax 层的输出产生的,因此权重总和被限制为 1,即 Pk =0 (t; ) = 1。对于时间序列模型,方程式 (2.15) 的输出因此也可以解释为使用注意力层在每一步提供的权重,对时间特征进行加权平均。然后可以使用注意力权重分析来了解每个时间步特征的相对重要性。在 [53、55、76] 中进行了实例可解释性研究,其中作者使用具体示例来说明 (t;) 的大小如何指示哪些时间点对预测最重要。通过分析注意力向量随时间的分布,[54] 还展示了如何使用注意力机制来识别数据集中的持久时间关系——例如季节性模式。
(b) 随着时间的推移反事实预测和因果推理
除了理解网络学习的关系外,深度学习还可以通过在其观察数据集之外产生预测或反事实预测来帮助促进决策支持。反事实预测对于场景分析应用程序特别有用——允许用户评估不同的动作集如何影响目标轨迹。这从历史角度(即确定如果发生一组不同的情况会发生什么)和从预测角度(即确定要采取哪些行动来优化未来结果)都是有用的。虽然存在大量深度学习方法用于估计静态设置中的因果效应 [77、78、79],但时间序列数据集中的主要挑战是存在时间依赖性混杂效应。当可能影响目标的动作也以对目标的观察为条件时,这是由于循环依赖而产生的。如果不对时间相关的混杂因素进行任何调整,直接的估计技术可能会导致有偏差的结果,如 [80] 所示。最近,基于统计技术的扩展和新损失函数的设计,出现了几种在调整时间相关混杂的同时训练深度神经网络的方法。利用统计方法,[81] 扩展了治疗加权的逆概率( IPTW)流行病学边缘结构模型的方法——使用一组网络来估计治疗应用概率,以及一个序列到序列模型来学习无偏预测。 [82] 中的另一种方法扩展了 G 计算框架,使用深度学习联合建模目标和动作的分布。此外,[83] 中提出了新的损失函数,它采用域对抗训练来学习患者病史的平衡表示。
5. 结论和未来方向
随着近年来数据可用性和计算能力的增长,深度神经网络架构在预测跨多个领域的问题方面取得了很大的成功。在本文中,我们调查了用于时间序列预测的主要架构——突出了神经网络设计中使用的关键构建块。我们研究了它们如何将时间信息结合到一步预测中,并描述了如何扩展它们以供使用在多层次预测中。此外,我们概述了混合深度学习模型的最新趋势,该模型结合了统计和深度学习组件,在任一类别中都优于纯方法。最后,我们总结了两种可以扩展深度学习以随着时间的推移改进决策支持的方法,重点放在可解释性和反事实预测方面的方法。尽管已经为时间序列预测开发了大量的深度学习模型,但仍然存在一些局限性。首先,深度神经网络通常需要以固定间隔离散化时间序列,这使得难以预测观察可能缺失或以随机间隔到达的数据集。虽然一些关于连续时间模型的初步研究已经通过神经常微分方程 [84] 完成,但还需要做更多的工作来将这项工作扩展到具有复杂输入(例如静态变量)的数据集,并将它们与现有模型进行基准测试。此外,如 [85] 中所述,时间序列通常具有层次结构,在轨迹之间进行逻辑分组——例如,在零售预测中,同一地区的产品销售可能会受到共同趋势的影响。因此,开发明确说明此类层次结构的架构可能是一个有趣的研究方向,并有可能提高现有单变量或多变量模型的预测性能