基于spss的曲线回归(curvilinear regression)
基于spss的曲线回归
- 一、简介
-
- 1、线性回归
- 2、曲线回归
- 3、非线性回归
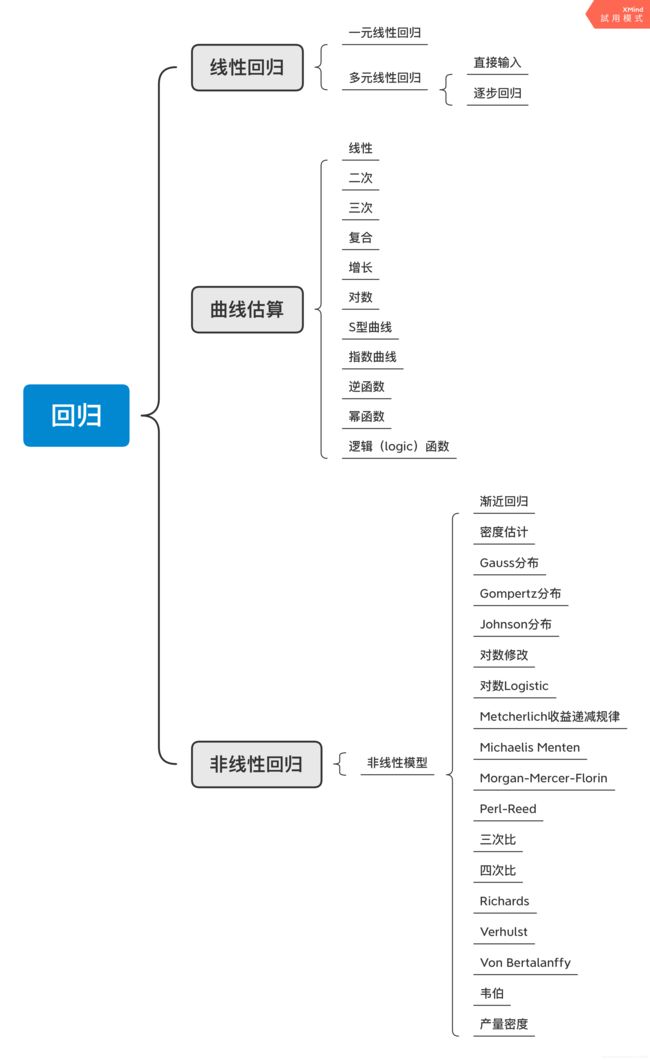
- 4、分类
- 二、曲线回归
-
- 1、曲线直线化
- 2、曲线估计
- 3、基本曲线的类型和特点
-
- (1)指数函数
- (2)对数函数
- (3)幂函数
- (4)双曲函数曲线:变形双曲线
- (5)S型曲线
- 4、步骤
- 三、基于spss的操作
-
- 1、判断分布趋势
- 2、曲线估计
- 3、对拟合程度优秀模型进行检验
- 4、总结
- 参考文献:
一、简介
我们常用的回归分析包括线性回归,曲线回归和非线性回归。
1、线性回归
回归分析根据自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析;按照自变量的数量,可分为一元回归分析和多元回归分析。如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析就称为一元线性回归分析;如果包括两个或两个以上自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
例如: y = a + b 1 x + b 2 x + ε y=a+b_{1}x+b_{2}x+{\varepsilon } y=a+b1x+b2x+ε,其中a表示截距,b表示直线斜率, ε {\varepsilon } ε表示误差项。
应用方向举例:在中学时期学习的在匀速运动中,时间与路程之间的关系;超市里,销量与销售额的关系,这些关系都是简单的线性关系。
2、曲线回归
现实生活中,许多事物之间的关系并非简单的线性关系,而是呈现某种非线性关系。非线性关系又可分为本质线性关系和本质非线性关系。本质线性关系是指变量关系在形式上虽然非线性关系,但可以通过变量转换转化为线性关系,并最终进行线性回归分析。而本质非线性关系则无法通过变量转换从而进行线性回归分析。曲线回归能够解决本质线性关系的问题。
本质是线性相关关系的变量,可以选择恰当的曲线方程将变量进行转换,实现曲线直线化,从而将曲线方程转化为直线回归方程进行分析。曲线估计模块能够自动拟合线性模型、对数曲线模型、二次曲线模型、指数曲线模型等多种曲线模型,而输出的统计量包括模型的回归系数、复相关系数、调整的拟合指数及方差分析结果等。
应用方向举例:在常人理解,某种商品的价格越低,销售量越大,价格越高,销售量越小,是呈直线关系的,其实,销售结果却不是常人理解的那样,可能销售价格低到某个值时,销量就不再上升,价格涨到某个值时,销量也不在下降,在二维坐标中,可能是一条曲线。
3、非线性回归
前面提到,非线性关系可以分为本质线性关系和本质非线性关系。可以通过变量装换转化为线性关系,并最终进行线性回归分析的叫本质线性关系;而无法通过变量装换转化为线性关系,最终也无法进行线性回归分析的叫本质非线性关系。这里说的非线性回归就是本质非线性关系。
曲线估计只能用于一个自变量和因变量相关关系的模型的分析,而非线性回归分析可以用来探讨因变量和一组自变量之间的非线性相关模型。线性回归模型要求变量之间必须是线性关系,曲线回归只能处理能够通过变量转换转化为线性关系的非线性问题,因此,这些方法都有一定的局限性。
非线性回归可以估计因变量和自变量之间任意关系的模型,可以根据自身需要随意设定估计方程的具体形式(神经网络的基础)。因此,非线性回归在实际应用中价值更大,应用范围更广。
应用方向举例:在现代的农业生产中,化肥的使用量与农作物的产量之间,在大多数情况下是非线性关系的。
4、分类
二、曲线回归
1、曲线直线化
如果面对某些变量的关系是非线性关系(曲线关系)时,最直接的方法就是曲线直线化,==曲线直线化的基本原理是将变量进行变换,从而将曲线方程化为直线回归方程进行分析。==例如通过散点图观察数据点的分布情况,或者根据前人的文献参考,某个现象的两个变量服从变换模型:

基本变化如下:
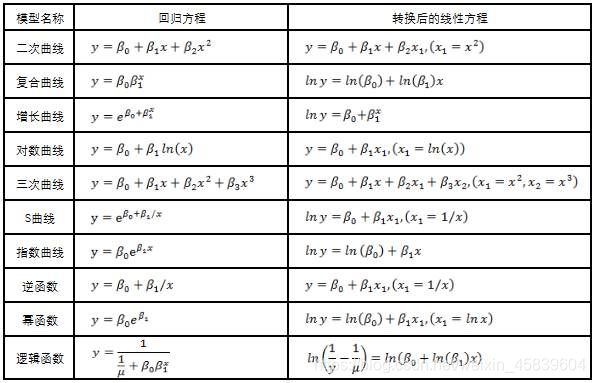
2、曲线估计
对直线化处理后的数据进行估算,这点可以由spss软件来进行制作,具体步骤如下:
- 绘制散点图,并观察散点图的分布特征以判断类似于何种函数;
- 根据所选定的函数进行变量转换;
- 对转换后的数据建立直线回归模型;
- 拟合多个模型,并通过比较各模型之间的拟合优度选择最合适的模型;
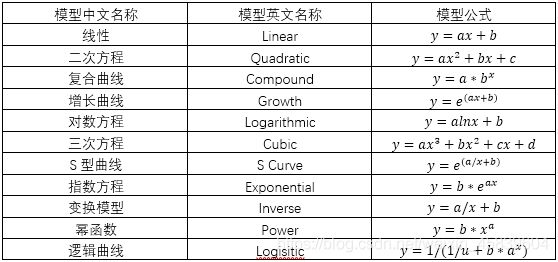
具体模型公式有:
3、基本曲线的类型和特点
(1)指数函数
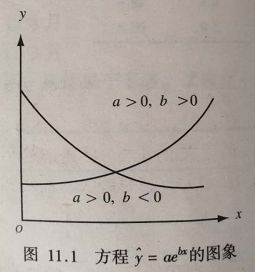
指数函数(x 作为指数出现)方程形式: y ^ = a b x \hat{y}=ab^{x} y^=abx 参数b一般用来描述增长或衰减的速度;
当 a>0、b>0时,y随x的增大而增大(增长),曲线凹向上;
当 a>0、b<0时,y随x的增大而减小(衰减),曲线也是凹向上。
(2)对数函数
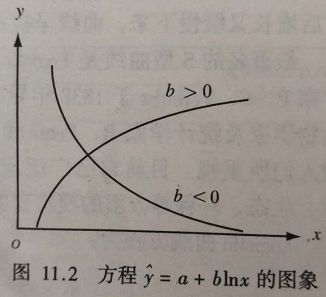
对数函数(x 作为自然对数出现)方程形式: y ^ = a + b I n x ( x > 0 ) \hat{y}=a+bInx (x>0) y^=a+bInx(x>0) 对数函数表示:x变数的较大变化可引起y变数的较小变化。
b>0时,y随x的增大而增大,曲线凸向上;
b<0时,y随x的增大而减小,曲线凹向上。
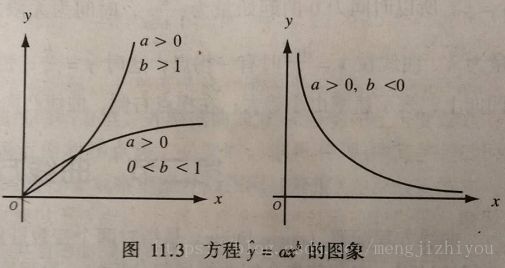
(3)幂函数
对数函数(y是x某次幂的函数)方程形式: y ^ = a x b \hat{y}=ax^{b} y^=axb
当 a > 0 、 b > 1 a>0、b>1 a>0、b>1时,y随x的增大而增大(增长),曲线凹向上;
当 a > 0 、 0 < b < 1 a>0、0
当 a > 0 、 b < 0 a>0、b<0 a>0、b<0时,y随x的增大而减小,曲线凹向上,且以x,y轴为渐近线。
(4)双曲函数曲线:变形双曲线
方程形式:
I . y ^ = x a + b x I.\hat{y}=\frac{x}{a+bx} I.y^=a+bxx I I . y ^ = a + b x x II.\hat{y}=\frac{a+bx}{x} II.y^=xa+bx I I I . y ^ = 1 a + b x III.\hat{y}=\frac{1}{a+bx} III.y^=a+bx1
其中: y ^ = x a + b x \hat{y}=\frac{x}{a+bx} y^=a+bxx , 该曲线通过原点(0,0)
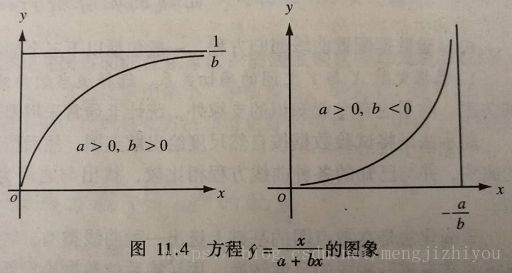
当 a>0、b>0时,y随x的增大而增大,但速率趋小,曲线凸向上,并向 y = 1 / b y=1/b y=1/b渐进;
当 a>0、b<0时,y随x的增大而增大,速率趋大,曲线凹向上,并向 x = − a / b x=-a/b x=−a/b渐进。
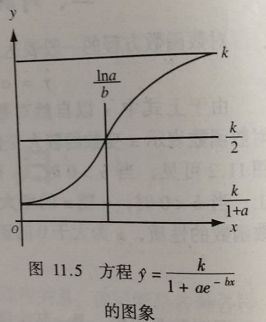
(5)S型曲线
主要描述动、植物的自然生长过程,又称生长曲线。
生长过程的基本特点是开始增长较慢,而在以后的某一范围内迅速增长,达到一定的限度后增长又缓慢下来,曲线呈拉长的‘S’型曲线。‘著名的S’型曲线是Logistic生长曲线。
Logistic曲线方程: y ^ = k 1 + a e − b x \hat{y}=\frac{k}{1+ae^{-bx}} y^=1+ae−bxk (a、b、k均大于0)
当x=0时: y ^ = k 1 + a \hat{y}=\frac{k}{1+a} y^=1+ak当 x → ∞ x\rightarrow\infty x→∞, y ^ = k \hat{y}=k y^=k 所以时间为0的起始量为 k 1 + a \frac{k}{1+a} 1+ak,时间为无限延长的终极量为 k k k。
曲线 x = l n a b x=\frac{lna}{b} x=blna时有一个拐点,这时 y ^ = k 2 \hat{y}=\frac{k}{2} y^=2k,恰好是终极量 k k k的一半。
拐点左侧,曲线凹向上,速率由小趋大;拐点右侧,曲线凸向上,速率由大趋小。
4、步骤
1.利用散点图,初步判断曲线类型
这要求大家熟悉曲线的形状。由于在具体的回归分析中,可能的曲线类型种类繁多,为了减少曲线估计的盲目性,通常先用散点图观测自变量与因变量之间的关系,判定因变量与自变量是否存在清晰的逻辑关系。如果散点图中的散点向曲线附近几种,比较接近于一条曲线,则初步判断可以做曲线回归分析,否则无法做曲线估计。对于可作曲线估计的数据,先认真观察曲线的形状,判定大概属于哪类曲线,是抛物线,还是对数曲线、指数曲线。
2.执行曲线回归分析
启动曲线估计功能,在“曲线估计”的配置界面下,正确地设置因变量和自变量,并可同时选择若干种曲线类型。在完成了曲线回归的计算机处理后,根据计算机的输出结果,参考判定系数R方值和检验概率Sig值,选择最恰当的曲线类型。
3.最后根据曲线类型的各个系数值,写出最终的函数式。
三、基于spss的操作
1、判断分布趋势
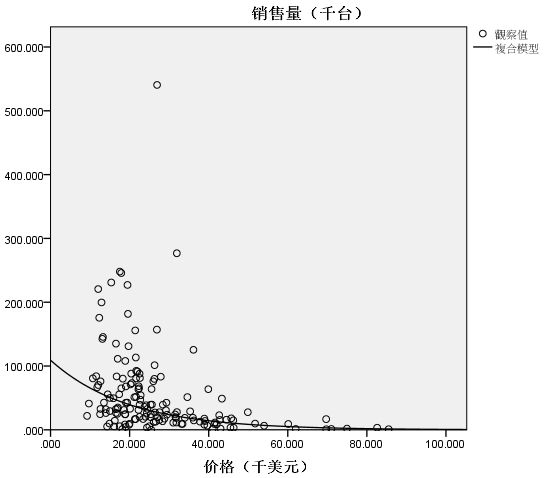
作散点图,观察变量是否存在线性关系:
【图形】-【旧对话框】-【散点/点状】-【简单分布】
结果解释:
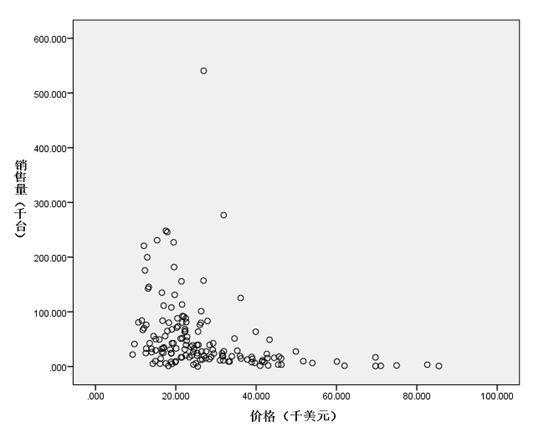
从散点图可知,自变量和因变量之间不存在线性关系,因此线性回归分析来构建售价和销量之间的函数关系,尝试使用选择曲线函数来找出汽车销售量与汽车销售价格之间的关系模型。
2、曲线估计
选择菜单【分析】-【回归】-【曲线估计】,勾选【模型】(想要进行估计的模型全部勾上,尽可能多试几个),勾选【绘图】和【等式中包含常量】,【保存】-勾选【预测值】、【残差】
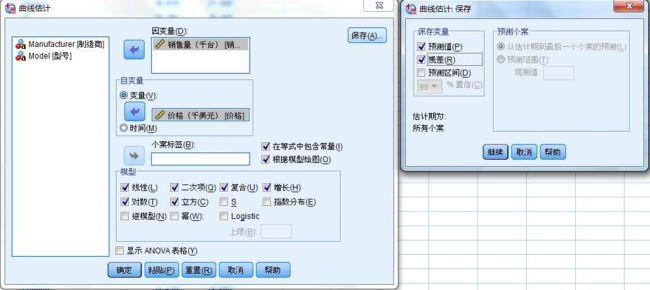
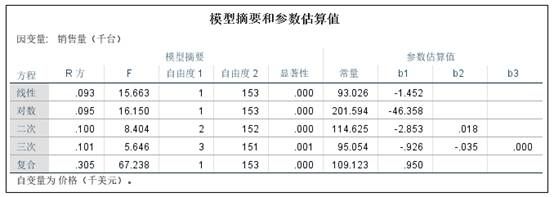

结果分析:
从分析结果来看,在所有曲线模型中复合曲线的R^2最大,为0.305,卡方检验的概率P值为0.000,说明拟合得到的回归系数有效,由此可知复合曲线较好地拟合了汽车价格和销售量之间的关系。同时,散点图也显示复合曲线更符合变量点的分布情况,拟合效果更好。
3、对拟合程度优秀模型进行检验
用复合曲线再次拟合数据;重复步骤2的过程,在模型中只选择复合曲线,同时选中显示ANOVA表格,点击确定。数据结果如下:
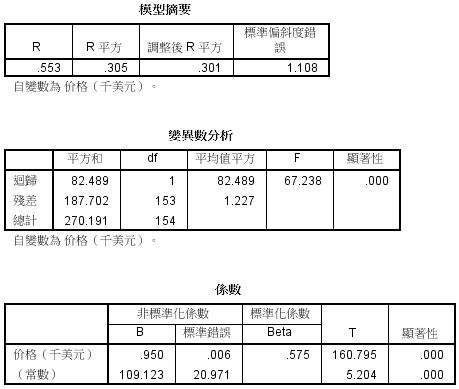
结果分析:
复合曲线的拟合度的R方为0.305,调整后的R方为0.301,说明该模型可以解释因变量的30.1%的差异,与1相比,效果不是非常的理想。复合曲线模型的方差分析F检验的显著性和回归系数t检验的显著性均为0.000,达到显著水平。综合以上结果,说明复合曲线对这份数据的拟合情况不是非常的理想,但是可以作为今后销售的参考。从拟合曲线与散点的分布情况可知,当售价大于30000美金时,拟合效果更好,所以用该模型预测售价大于30000美金的型号更为准确。该模型的回归方程为: 销 售 额 = 109.123 ∗ 0.95 0 售 价 销售额=109.123*0.950^{售价} 销售额=109.123∗0.950售价
4、总结
用回归方程进行预测忌讳迷信拟合指标结果,应该将拟合的指标结果与拟合图形结合,观察那个区间的自变脸拟合的因变量比较好,机动灵活的使用回归分析。
参考文献:
[1]csdn作者mengjizhiyou:曲线回归------(一)曲线的类型与特点及方程的配置
[2]简书作者spssau:曲线回归分析
[3]微信公众号生活统计学:SPSS分析技术:曲线回归