CAE 分析中 隐式和显式时间积分算法的python程序实现
前两天,同事研究Dyna的显/隐式时间积分的差异和基本原理。想来自己也有三、四年没做这方面的编程了,对同事问的一些问题也一时犯迷瞪,索性就又看了一遍书,网上找了些资料,写了点代码,理了理思路,以备不时之需。
0.前言
物理世界中,最常见的运动形式是由质量、阻尼和弹簧组成的运动系统,如图1所示,而且对应的运动方程如式1所示。
(1)
式中,u为位移,其一阶倒和二阶倒分别为速度和加速度,而M,C,K分别为质量,阻尼和弹簧的刚度,F则为外部载荷。
该方程也可以写成式2的形式:
(2)
其中,![]() 为惯性力,为阻尼力,
为惯性力,为阻尼力,![]() 为弹簧力,Fext为外部力。可以知道,Fk为弹簧变形引起的力量,可以认为是系统内部力量,而
为弹簧力,Fext为外部力。可以知道,Fk为弹簧变形引起的力量,可以认为是系统内部力量,而![]() 和不会引起系统自身的变形,因此可认为是外力的一部分。
和不会引起系统自身的变形,因此可认为是外力的一部分。
由式1可知,运动系统方程是一个常微分方程(ODE),它的时间积分方法包括隐式积分和显式积分,这两种方法的差异在于,预测时间步和当前时间步的位移、速度和加速度之间的关系。如果,预测时间步(t+Δt)的某个变量需要考虑预测时间步(t+Δt)其他的变量,为隐式;相反,如果预测时间步(t+Δt)的变量与自身无关,至于上个时间步有关(t),则为显式。
1. 隐式时间积分
隐式积分方法有很多种,包括了我们常见的龙格库塔等方法。但在dyna中用的隐式方法为Newmark法,该方法通过将M和C引起的惯性力和阻尼力,引入两个参数![]() 和
和![]() ,从而将运动方程中的惯性力和阻尼力两项转换成了有效刚度和外部力两部分,从而运动方程转换成式3的形式。
,从而将运动方程中的惯性力和阻尼力两项转换成了有效刚度和外部力两部分,从而运动方程转换成式3的形式。
(3)
其中,和![]() 如下。
如下。
(4)
(5)
式中,K为关于位移u的函数,F为关于时间t的函数。
a1 = m/(beta*deltaT*deltaT) + gamma *c/(beta*deltaT)
a2 = m/(beta*deltaT) + c*(gamma/beta-1)
a3 = m*(1./(2*beta)-1) + deltaT*c*(gamma/(2*beta)-1)
# effective stiffness & force k_*u=f_
k_ = klin(u) + a1
f_ = flin(t) + a1*u + a2*du + a3*ddu通过求解式3,可以获得下一时间步的位移,并计算的到该位移乘以刚度所得弹簧变形力,以及相应的惯性力和阻尼力,并与下一时间步对比来确保力的平衡,保证每一时间步下的求解精度。而这一过程是方程求根的过程(也可以认为是寻找最优解的优化问题),因此可以采用Newton-Raphson迭代获得方程(式3)的根。当满足收敛准则(Rn 迭代算法程序如下: 当计算得到收敛后的(即下一时间步的位移),便可以预测下一时间步的速度和加速度,如下所示。 在获得了,和,便可以作为下一时间步的初值,循环反复得到系统的瞬态响应。具体流程如下: 中心差分法与Newmark最大的差异在于: 该方法不求解的方程,而是求解获得加速度值,并由前一时间步的速度,预测出下一时间步的速度,进一步得到位移值。在不考虑阻尼力的情况下,内力来自于弹簧刚度k与位移u的乘积,而 时间积分方法的两个基本要求,一个是计算的稳定性,一个是计算的准确性。为了验证显式和隐式的稳定性和准确性,选择一个算例用于验正是很有必要的,本文算法参考的模型来自于(W. T. Thomson, Vibration Theory and Applications, 2nd Printing, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1965, pp. 98-99.),ANSYS 手册中VME1。 时间积分的稳定性组要体现在,计算过程会不会发散,即求解得到结果Rn无法小于收敛容差,这往往取决于不同算法的稳定性要求: Newmark稳定性的判断,需要写出系统的传递矩阵(如图7),其特征值计算程序如下: 选取不同 可以得到该系统的三个特征值,根据李雅普诺夫第一法,该系统有一个零特征值,两个有负实部共轭特征值,因此系统为临界稳定。 可以通过对不同参数演变过程的观察,可以判断不同积分算法的准确度。当 代码中用到了闭包去获得线性插值函数,用到了递归实现Newmark时间积分。原程序下载 https://wenku.baidu.com/view/7cabca2e2f3f5727a5e9856a561252d381eb2051 https://ww2.mathworks.cn/matlabcentral/answers/341514-newmark-s-method-for-nonlinear-systems?requestedDomain=zh![]() 图3 Newton-Raphson迭代
图3 Newton-Raphson迭代
# Newton-Raphson
while abs(Rn) > TOL: #Iteration convergence
k_= k_ + a1
dun = Rn/k_
un = un + dun
Rn = f_ - klin(un)*un- a1*un
# print 'Tolerance:',abs(Rn/klin(un))# Next velocity and acceleration predict
dun = gamma*(un-u)/(beta*deltaT) + du*(1-gamma/beta) + deltaT*ddu*(1-gamma/(2*beta))
ddun = (un-u)/(beta*deltaT*deltaT) - du/(beta*deltaT) - ddu*(1./(2*beta)-1)2. 显式时间积分——中心差分法
![]() 来自与外部力和惯性力。
来自与外部力和惯性力。################Force###############
def CenterDiff(t,endtime,m,u,delta,du0):
fext = flin(t)
fint = klin(u)*u
ddu = (fext - fint)/m
du = du0 + ddu * delta
u = u + du*delta
t+=delta 3.算法稳定性和精度对比
3.1 对比算例
3.2 稳定性
![]() 图6 不同算法稳定性要求
图6 不同算法稳定性要求
import sympy as sp
import numpy as np
beta_val = 0
gamma_val = 0.5
sp.var(['dt','wc','beta','gamma'])
A = sp.Matrix([[1.,0.,-beta*dt*dt],[0.,1.,-gamma*dt],[wc*wc,0.,1.]])
B = sp.Matrix([[1.,dt,(0.5-beta)*dt*dt],[0.,1.,(1.-gamma)*dt],[0.,0.,0.]])
C = A.inv() * B
A_eigen = C.subs([(beta,beta_val),(gamma,gamma_val)])
res = A_eigen.eigenvals()
print (res)
# -dt**2*wc**2/2 - dt*wc*sqrt((dt*wc - 2)*(dt*wc + 2))/2 + 1
# -dt**2*wc**2/2 + dt*wc*sqrt((dt*wc - 2)*(dt*wc + 2))/2 + 1
#谱半径小于1 Ax=B 矩阵求解过程收敛
ct1 = abs(-dt**2*wc**2/2 - dt*wc*sp.sqrt((dt*wc - 2)*(dt*wc + 2))/2 + 1) <= 1
print (ct1.subs(dt,2./wc))
ct2 = abs(-dt**2*wc**2/2 + dt*wc*sp.sqrt((dt*wc - 2)*(dt*wc + 2))/2 + 1)<= 1
print (ct2.subs(dt,2./wc))
sp.plot_implicit(ct1)
sp.plot_implicit(ct2)# -*- coding: utf-8 -*-
"""
Created on Tue Nov 20 12:41:40 2018
@author: yujin.wang
"""
import numpy as np
import matplotlib.pyplot as plt
import scipy as sci
import sys
gamma = 0.5
beta =0.25
k = 100.
m=1.
c=0
delta = 0.5
a = np.matrix([[1.,0.,-beta*delta*delta],[0.,1.,-gamma*delta],[k/m,0,1]])
b = np.matrix([[1.,delta,(1/2.-beta)*delta*delta],[0.,1.,(1.-gamma)*delta],[0,0,0]])
c = a.I*b
print np.linalg.eigvals(c)
#[-1.90808633e-16+0.j -7.24137931e-01+0.68965517j -7.24137931e-01-0.68965517j]![]() =0.5,0.05,0.005和
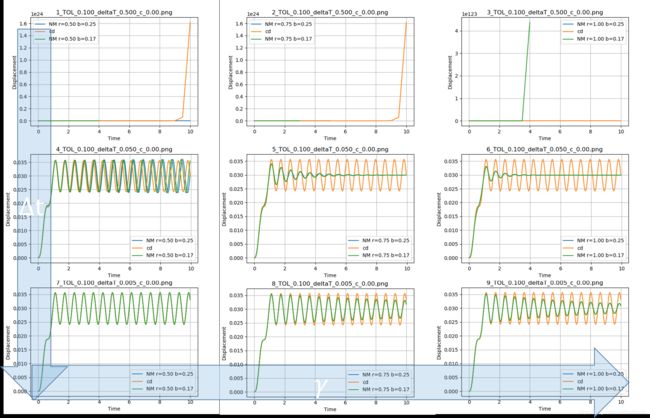
=0.5,0.05,0.005和![]() =0.5,0.75,1.0,分析得到的结果绘制于图8,图中还包括了中心差分法的计算结果(cd)。可以看出在
=0.5,0.75,1.0,分析得到的结果绘制于图8,图中还包括了中心差分法的计算结果(cd)。可以看出在![]() =0.5时,稳定性方面只有平均加速方法没有发散,而在
=0.5时,稳定性方面只有平均加速方法没有发散,而在![]() =0.5,0.75时,只有中心差分法发散。在
=0.5,0.75时,只有中心差分法发散。在![]() =0.5时,平均加速算法稳定,而线性加上速度则计算发散,如图9所示。
=0.5时,平均加速算法稳定,而线性加上速度则计算发散,如图9所示。 3.3 计算准确度
![]() =0.5时,Δt足够小时,中心差分法和Newmark法所得的结果基本一致,而当
=0.5时,Δt足够小时,中心差分法和Newmark法所得的结果基本一致,而当![]() >0.5时,Newmark将会引入数值阻尼,从而引起本应周期振荡的过程趋近于稳态解(忽略惯性力),并且Δt过大,会增加数值阻尼的作用。
>0.5时,Newmark将会引入数值阻尼,从而引起本应周期振荡的过程趋近于稳态解(忽略惯性力),并且Δt过大,会增加数值阻尼的作用。![]() 图9 Newmark 线性加速法和平均加速法稳定性对比
图9 Newmark 线性加速法和平均加速法稳定性对比
4. 完整代码
5.参考