摄像头内参准确性验证方法

前言

摄像头内参标定出来后，标定结果是否准确？有些内参准确性的验证方案需要很大的场地，且有很多误差源不好控制（特别是对视野比较大的摄像头），惠州市华阳数码特电子有限公司发明了一种占用场地小测试精度高的方法，已投入实际使用，效果良好。（本文文稿由华阳数码特提供）

目录：

一．M公司的内参验证方案简介

二．M公司内参验证方案的实施难点

三．华阳的解决方案-测平行光管的夹角

四．方向误差分布的测量方法

附一．求光线方向的算法

一

M公司的内参验证方法简介

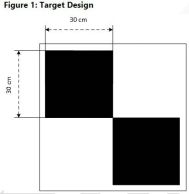
1．摄像头的入瞳中心与两个目标点之间的距离约20米，两个目标点之间的距离约10米，距离测量精度不低于2mm

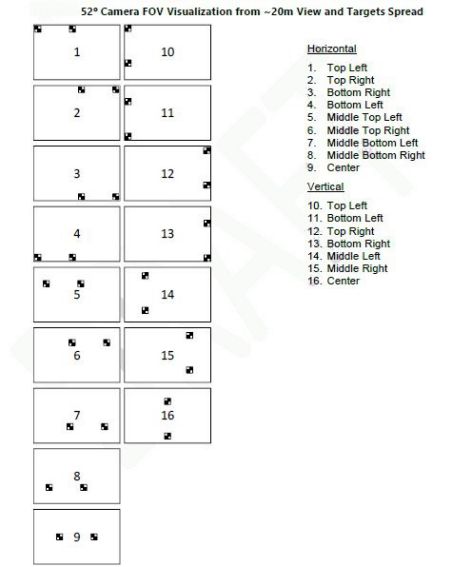
2 让两目标点水平或垂直成像在摄像头不同的视野区域（共16图）

3.提取两目标点的角点坐标（亚像素），根据内参值及摄像头入瞳中心与目标点的距离，计算出两目标点的距离（这与测两目标点与摄像头入瞳中心的夹角是等效的）

4.比较计算出的两目标点间的距离与实测距离的差异，用于判断内参的准确性

二

M公司内参验证方案的实施难点

1. 需要很大的场地（20多米 x 10多米）

2. 比较难测准摄像头入瞳中心与目标的距离 --长度测量设备比较难对齐摄像头入瞳中心（一般在摄像头第一镜片下几毫米的地方，是一个设计值）

3. 对于视野较大的摄像头，由于摄像头需要较大幅度的转动，比较难控制摄像头入瞳中心相对于转动中心的平移量。

三

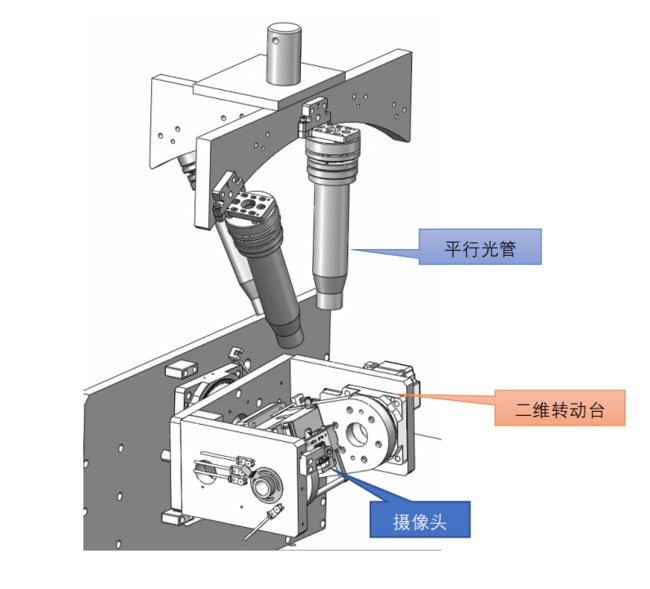
华阳的解决方案-测平行光管的夹角

用两根或多根平行光管（模拟距离无穷远）代替M公司方案的成像目标点，通过平行光管内十字鞍点的像坐标及内参值计算出平行光的方向（计算方法见附一），从而算出两平行光管的夹角，此计算出的夹角与平行光管间的实际夹角进行对比，确认内参的准确性

优点如下：

1.占用场地小

2.摄像头入瞳中心的平移，不影响测量结果（当然要求平行光管内的目标鞍点在摄像头视野内）

3.对摄像头的安装要求低，摄像头的转动中心与摄像头入瞳中心的重合性要求较低

4.还可以在转动机构的精度下，计算视场内多点的方向误差（见第四节）

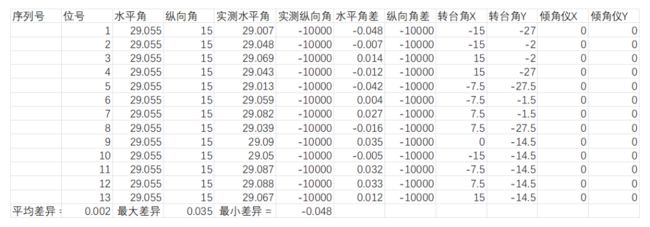
例子：两平行光管角度测量值及与实际值的差异：

例子中：-10000表示无效数值（目前只装了两只光管，没有装第三只光管），角度单位为“度”

四

方向误差分布的测量方法

当摄像头转动一定角度时，平行光管相对摄像头的方向与通过像点坐标及内参计算出的方向是有差异的，差异程度反映了内参的准确性。

这种测量方法与重投影误差的区别：

A: 误差不是在像素坐标系（像空间）下表示，而是在相机坐标系下（物空间）表示，更能反映由于内参的偏差造成物体方向判断的偏差程度

B: 本方法中虽然摄像头转动时，会取多张图，但这些图只对应一组外参（而不是传统方法中每张图卡有一组外参），也就是平行光管组相对于相机的初始方向（三个自由度的转动向量）是待求的，摄像头转动时，平行光管组相对相机的方向是根据转动的角度确定的。由于大大减少了优化算法的自由度，计算出的结果比传统的重投影误差更能说明内参是否准确。

具体而言，优化算法只有如下几个自由度：

1．平行光管组相对于相机坐标的初始方向（三个自由度）

2．转轴X在相机坐标下的方向向量（单位向量，两个自由度）

3．转轴Y在相机坐标下的方向向量（单位向量，两个自由度）

测试结果例：

方向差异分布图（采用极坐标，下面圆的半径对应FOV）

角度单位是度，测试精度0.06度（转台的转角精度）

红色虚线表示Sensor边界，箭头表示按像点坐标及内参计算的光线方向与实际光线方向的差异（箭头的长度相比FOV的刻度放大了20倍）

---

附一．利用像点坐标及内参计算光线方向的算法

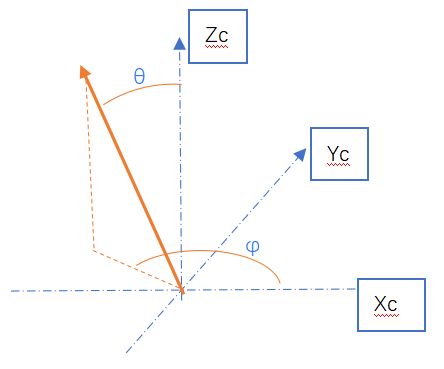
1．光线方向可以用一个单位向量来表示，因此用两个参数来表示，视角θ与方位角φ，Xc/Yc/Zc为相机坐标系

2．光线方向的单位向量为（sinθ*cosφ，sinθ*sinφ，cosθ），将此相机坐标代入畸变模型公式，就可列出两个方程，由于像点坐标（u, v）是已知的，通过解此两个非线性方程，可以求出θ与φ

以针孔模型为例，两个方程如下：

3．两个光管的单位向量求出后，通过两向量的点乘算出两向量夹角的余弦，进而算出两向量的夹角。