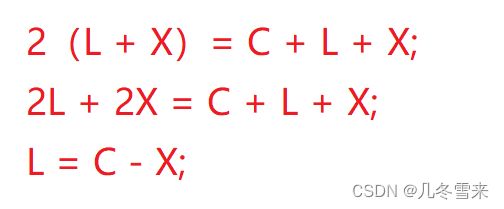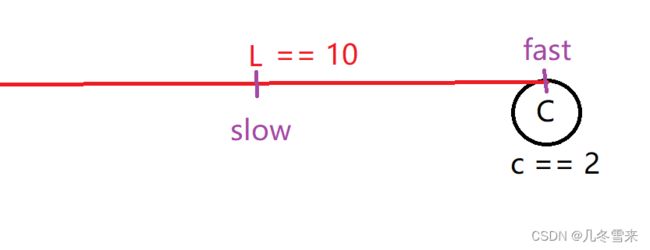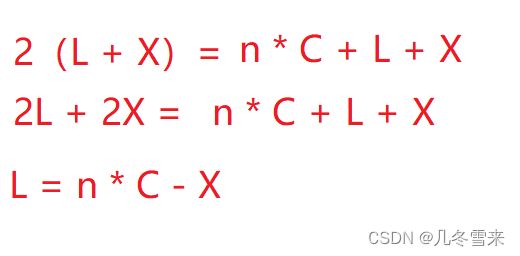数据结构——链表OJ题目讲解（3）

作者：几冬雪来

时间：2023年3月12日

内容：数据结构链表OJ题目讲解

来源：力扣

目录

前言： 

刷题：

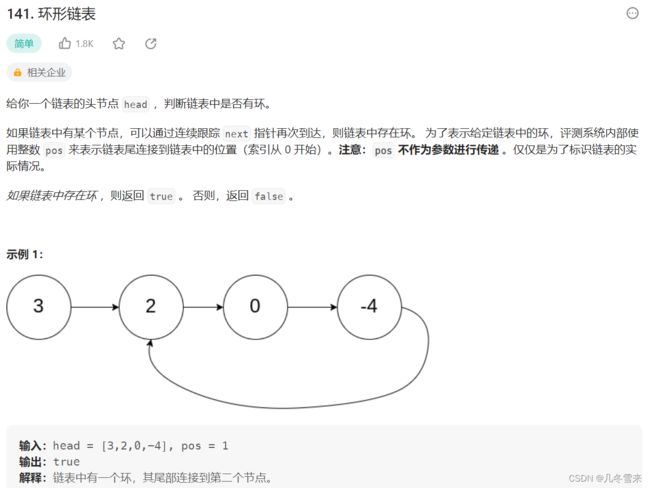
1.环形链表： 

2.环形链表2：

结尾：

---

前言： 

在上一篇博客中我们又讲解了几道链表的OJ题目，并从中学到了不同以往的解题思路，还有从未见过的解题方法——创建哨兵位的头结点。但是，到现在我们讲解的内容，这部分知识只不过是数据结构中链表问题的冰山一角罢了，而为了揭开它真正的面目，接下来我们将继续链表题目的讲解。

刷题：

刷题是我们做数据结构题目中必不可少的一步，通过刷题我们会了解到更多的知识。例如我们上一篇博客所讲解的——创建哨兵位头结点。那么今天下来我们依旧通过解题来了解我们的链表。

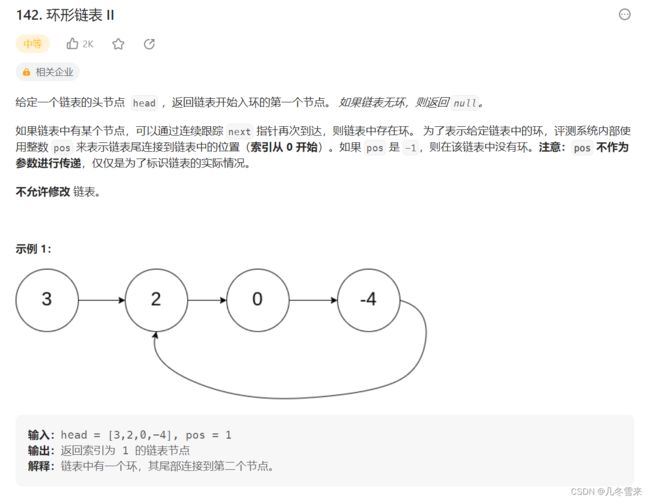
1.环形链表： 

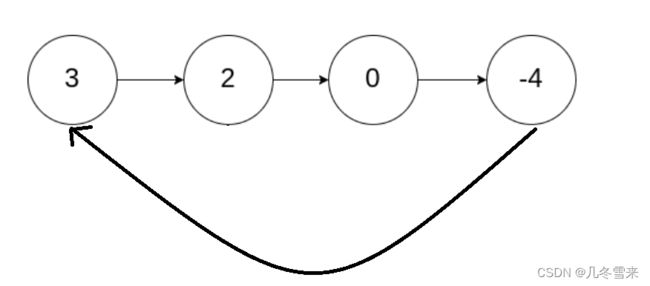
那么什么是带环链表呢？我们以上面的一个图为例修改后来举例，上面的示例并不是一个正经的带环链表。那么正经的带环链表是长什么样子的？

这种就是我们正经的带环链表，尾结点指向我们头结点的地址。 

那么我们的带环问题有什么存在坑的地方吗？ 我们的带环链表就有一个最根本的问题，如果我们的带环链表如果遍历的话，那就可能会死循环。

那么我们如果判断我们的链表是带环的呢？ 

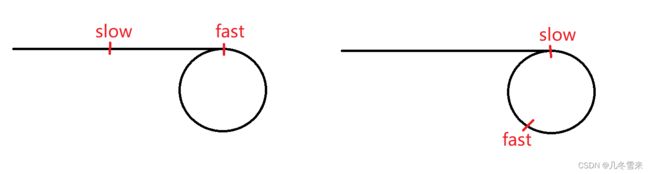
这里还是运用我们的快慢指针来解决这个问题。

这里我们创建一个快指针和一个慢指针，当慢指针走到链表一半的时候，快指针刚刚好进入环，当我们的慢指针刚进入环的时候，快指针已经在环里走了一段距离了，这个时候就会变成一个追击问题，什么时候快指针与慢指针相遇。 

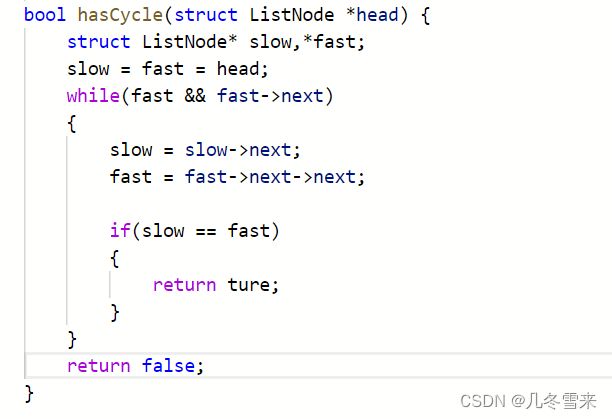
那接下来我们先把其代码写出来。

开始我们创建两个指针，两个指针都指向头结点。接下来就是判断，我们还是拿走得快的指针作为判断条件，如果fast或者fast->next不为空，我们的慢指针就向前走一步，快指针向前走两步，如果中间有哪个时候快指针和慢指针相等，早就说明它们相遇了，我们返回true，反之返回false。 

如果只是将这道题写出来的画，那么我们这个样子就已经结束了。不过，这并不是重点，我们根据这道题所延展出来的问题才是我们的重点。 

我们通过这道题延展出了两个新的问题。

1. 为什么slow走一步，fast走两步它们会相遇？会不会错过？

2.如果slow走一步，fast走n步（n>=3）它们会不会相遇？会不会错过？

那我们先解决第一个问题。

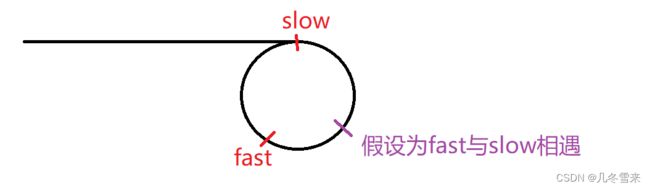
这里我们画个图，并假设在某处fast和slow相遇。（实际上哪里相遇取决于环的大小及前缀） 

在这里我们假设slow刚刚进入环的时候，fast到slow的距离为n，也就是追击距离为n。而后，slow每走一步，fast走两步，两个指针之间的距离n在不断的缩小，每次缩小1。到最后距离缩小到为0，那也就可以证明我们追击成功。

因此我们这里一定会相遇，并不会错过。

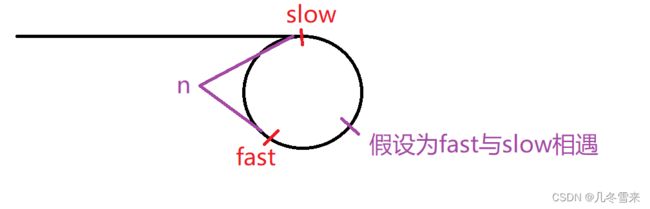
那么接下来就是我们的第二个问题。在这里假设如果fast每次走3步的话，我们还能追上吗？

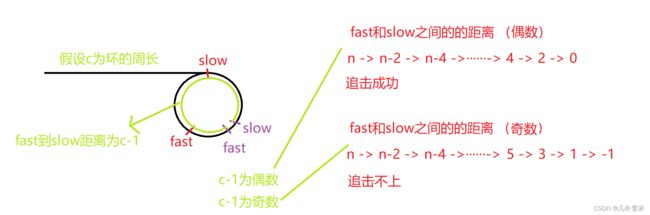
这里还是将slow刚进入环时，设fast到slow的距离为n，只不过这一次fast和slow之间的距离每次缩小2，那么这里就引申出了两个不同的结果。

当我们fast和slow之间的距离为偶数的时候，我们可以追击上；但是当它们的距离为奇数的时候，最后减出来的值并不为0，也就是说明没有追击上，fast在slow前面。当然这里还可以再追击一次。

因为第一次我们追击失败，fast要在slow前面一个位置，那么在这里我们就设我们环的周长为c，也就是fast到slow之间的距离为c-1。接下来我们又要对c-1进行分析，如果c-1为偶数那就可以追击上，要是为奇数那就追击不上。如果要在这个基础上再一次实现追击，我们fast和slow的距离还是c-1，又因为c-1为奇数，所以代码会陷入死循环。

因此现阶段我们并不能证明第二个问题是可以相遇的。

 在解决前两个问题的过程中，我们引出来了一个新的变量，也就是环的长度——c。每一个环的长度都是不一样的，有长的环也有短的环，那么我们有没有一个表达式来计算环的长度呢？

这里也是很简单的。

 

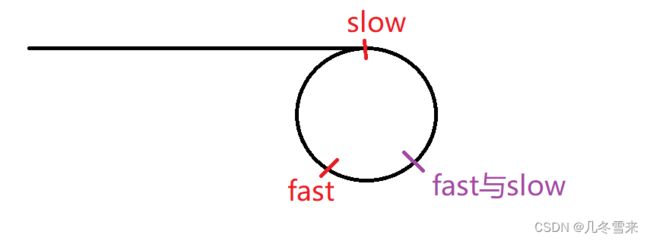
还是我们这个环，slow和fast在环的某处之后，这个时候就让fast固定不动，slow一步一步的往前走，当slow再次和fast相遇的时候，我们就可以计算出环的长度了。 

2.环形链表2：

这里的题目要求我们寻找链表的入口点。那怎么找到环的入口点又是一大问题。

 

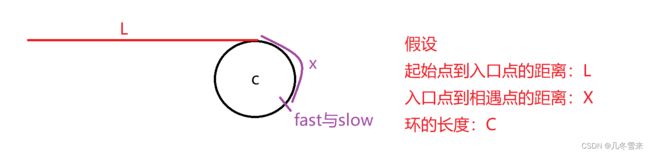
这里我们假设起始点到入口点，入口点到相遇点的距离分别为L和X，环的长度假设为C。

那么在这里slow从起始点到相遇点的距离为L+X。而当slow到相遇点的时候，fast已经可能在走了一圈了，因此我们可以将fast到相遇点的距离设为C+X+L。

又因为fast每次走两步，slow每次都一步导致fast走的距离是slow的两倍。明白了这个道理，我们就可以将两个式子联系起来。

 

最后得到这样的一个式子，但是很遗憾，这个式子是错误的，那么是哪里错误了，我们依旧可以画一张图来表示。

 

当我们的环的长度很小，起始点到入口点距离很大的时候，如果slow刚刚到入口点的话，fast可以已经走了很多圈了。所以我们的式子要进行修改。

因为fast可以走了n圈（n >= 1），在这里我们要求C加上一个前缀。 

那么我们可以简单的得到一个结论，假设n为1。那式子就变成了L = C + X。

结论：一个指针从相遇点走，一个指针从起始点走，它们会在入口点相遇。

下来就应该写代码了。

 

这个就是我们的代码了。

老规矩，一开始先创建两个指针，并让它们指向头结点。接下来就是循环slow指针一次走一步fast指针一次走两步。如果二者相遇，我们就再创建两个指针，一个指针指向slow，也就是二者相遇的位置，另一个指针指向头结点。如果它们不相等，则各自往后走一步最后相等返回meet位置的指针。要是一开始循环条件不成立，我们就直接返回空。

当然这道题我们也有另一种解决方法。

 

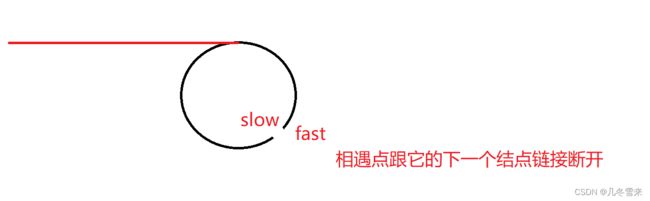
这里可以将相遇点和下一个结点断开，而后相遇点的下一个结点设成一个新的头结点，这个新的头结点和原先链表的头结点就可以构造成链表中的找链表交点的问题。 

那么这种方法的代码又该怎么写呢？

这里我们在上方引入了求交点的函数，但是这里并没有写出来，大家要注意。

这里对代码进行了修改，当两个指针相遇。这里我们将slow的地址给meet，然后创建两个指针，一个指向meet下一个结点，另一个指向链表的头结点，接下来将meet->next置空，最后进入找交点的函数，并返回交点的值即可。

结尾：

 经过几道题目的讲解，我们对链表的理解更强了几分。但是我们依旧没有真正意义上的完全掌握链表的知识，要进一步提升链表的知识靠的不仅是刷题，还有平常的积累，同时我们的链表有8种类型，每一种不同类型的链表可能就会诞生出一种全新的解法。最后希望这篇博客可以为刷题的同学带来帮助。