算法通关村第8关——二叉树的经典算法题（青铜）

1. 二叉树里的双指针

1.1 判断两棵树是否相等

leetcode 100. 相同的树

这里其实就是两个二叉树同时进行前序遍历，先判断根节点是否相同， 如果相同再分别判断左右子节点是否相同，判断的过程中只要有一个不相同就返回 false，如果全部相同才会返回true。其实就是这么回事。

public boolean isSameTree(TreeNode p, TreeNode q) {
	// 如果两个二叉树都为空，则认为相同
	if(p == null && q == null){
    	return true; 
    }
    
   // 如果其中一个二叉树为空而另一个不为空，则认为不相同
    if(p == null || q == null){
        return false;
    }
    
    // 如果两个二叉树的根节点的值不相等，则认为不相同
    if(p.val != q.val){
        return false;
    }
    
    // 递归判断两个二叉树的左子树和右子树是否相同
    return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}

1.2 对称二叉树

leetcode 101. 对称二叉树

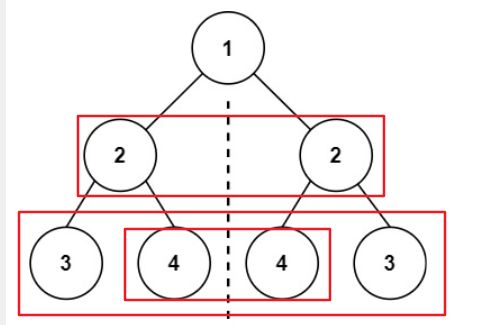
其实这一题就是上一题的变式，过程大差不差，需要理解一个地方，就是比较的时候，比较哪个部分

也从图和题意就能看出，其实比较的是root的左右子树，那么下一步比较的是：

1. 左子树的左子树，与，右子树的右子树
2. 左子树的右子树，与，右子树的左子树

则，满足这个条件，就是对称二叉树

代码就如下啦：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return check(root.left, root.right);
    }

    public boolean check(TreeNode leftNode, TreeNode rightNode){
        if(leftNode == null && rightNode == null){
            return true;
        }

        if(leftNode == null || rightNode == null){
            return false;
        }

        if(leftNode.val != rightNode.val){
            return false;
        }

        return check(leftNode.left, rightNode.right) && check( leftNode.right, rightNode.left);
    }
}

1.3 合并二叉树

leetcode 617. 合并二叉树

这题的思路其实就是指针，有点像之前的链表题，只需要指过去就相当于添加

思路：

1. 首先，考虑边界情况。如果其中一个二叉树为空，那么合并后的结果就是另一个非空的二叉树。这是一个递归的终止条件。
2. 接下来，创建一个新的节点，作为合并后的二叉树的根节点。将根节点的值设置为两个二叉树根节点值的和。
3. 递归地合并两个二叉树的左子树和右子树。递归调用过程中，需要创建新的节点，并将其赋值给对应的左子节点和右子节点。
4. 最后，返回合并后的二叉树的根节点。

思考方式上，可以从树的根节点开始，逐层向下思考。首先考虑根节点的处理，然后再递归地处理左子树和右子树。在处理子树时，可以使用相同的思考方式来处理子树的根节点、左子树和右子树。

代码：

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null){
            return root2;
        }
        if(root2 == null){
            return root1;
        }
        TreeNode res = new TreeNode(root1.val + root2.val);
        res.left = mergeTrees(root1.left, root2.left);
        res.right = mergeTrees(root1.right, root2.right);   
        return res;
    }
}

不过这段代码需要每次new的时候将值赋值进去，可以进行优化

优化方法如下：

1. 在判断树是否为空时，先判断根节点是否为空，再判断左子树和右子树是否为空。这样可以减少判断的次数。
2. 如果两个树中只有一个树为空，那么可以直接返回另一个非空树作为合并后的结果，无需继续递归。
3. 在创建新节点时，可以不立即赋值，而是在递归调用后再赋值。这样可以减少节点的创建次数。

基于以上优化，可以得到以下代码：

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null){
            return root2;
        }
        if(root2 == null){
            return root1;
        }
        
        TreeNode res = new TreeNode(0);
        res.left = mergeTrees(root1.left, root2.left);
        res.right = mergeTrees(root1.right, root2.right);   
        
        res.val = root1.val + root2.val; // 在递归调用后再赋值
        
        return res;
    }
}

这样在leetcode上面执行就会发现快很多~

2. 路径专题

2.1 二叉树的所有路径

leetcode 257. 二叉树的所有路径

这题要慢慢思考，整理，我觉得需要注意以下的思考题目的地方：

1. 不一定一次遍历到底，之前学的遍历可以一次递归，但是这题如果使用两次左右子树递归会更加方便
2. 掌握递归的三要素，边界，结束条件，核心代码。按照这个方式才写的好。

lass Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        treePaths(root, "", res);
        return res;

    }

    public void treePaths(TreeNode root, String path, List<String> res){
        if(root == null) return;
        if(root.left == null && root.right == null){
            res.add(path + root.val);
            return;
        }
        treePaths(root.left, path+root.val+"->", res);
        treePaths(root.right, path+root.val+"->", res);
    }
}

不过还可以再优化，就是String这里。

1. 可以使用StringBuilder代替String进行路径拼接。String对象是不可变的，每次拼接都会创建新的String对象，而StringBuilder对象是可变的，可以在原地进行字符串拼接，效率更高。
2. 考虑到输入的二叉树可能为空，可以在方法开始处添加一个判断条件，如果根节点为空，则直接返回空结果列表。

不过这里就会导致需要了解一个叫做回溯的算法思想

回溯是一种算法思想，常用于解决组合、排列、子集等问题。在回溯算法中，我们通过递归的方式尝试所有可能的解，并在每次递归结束后撤销操作，回退到上一个状态，继续尝试其他可能的解。

在这个特定的问题中，当遍历二叉树时，我们需要构建一条路径来表示从根节点到叶子节点的路径。为了构建路径，我们使用了StringBuilder来拼接路径中的节点值和箭头符号。但是，在递归回溯时，为了保证每次递归调用都能得到正确的路径，需要将StringBuilder的长度恢复到之前的长度。这样做是因为在递归过程中，我们反复使用同一个StringBuilder对象，如果不进行回溯，下一次递归调用会基于上一次递归调用的结果进行拼接，导致结果错误。

简而言之，回溯的目的是为了确保每次递归调用都是在干净的状态下进行，避免对之前的状态产生影响，从而得到正确的解。在这个问题中，回溯的作用是恢复StringBuilder的长度，使其在每次递归调用时都是空的，然后再重新构建路径。

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        dfs(root, new StringBuilder(), res);
        return res;
    }

    private void dfs(TreeNode root, StringBuilder path, List<String> res) {
        if (root == null) {
            return;
        }
        int len = path.length();
        path.append(root.val);
        if (root.left == null && root.right == null) {
            res.add(path.toString());
        } else {
            path.append("->");
            dfs(root.left, new StringBuilder(path), res);
            dfs(root.right, new StringBuilder(path), res);
        }
        path.setLength(len); // 回溯，恢复path的长度
    }
}

2.2 路径总和

112. 路径总和

本题询问是否存在从当前节点root 到叶子节点的路径，满足其路径和为 sum，假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题: 是否存在从当前节点的子节点到叶子的路径满足其路径和为 sum - val。
不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可 (因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件)。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可。

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null){
            return false;
        }
        if(root.left == null && root.right == null ){
            return targetSum == root.val;
        }

        boolean left = hasPathSum(root.left, targetSum - root.val);
        boolean right = hasPathSum(root.right, targetSum - root.val);
        return left || right;
    }
}

3. 反转的妙用

3.1 反转二叉树

226. 翻转二叉树

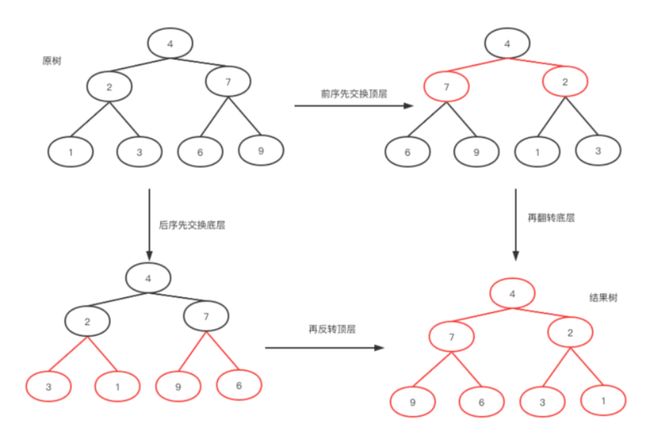
简单画个图，我们就可以了解到其实只要每次都反转左右节点即可

那就有三种方法：

1. 前序遍历：从上往下左右节点交换
2. 后序遍历：从下往上交换
3. 迭代

前序遍历方法

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;

        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

后序遍历方法

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}

迭代方法

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode current = queue.poll();
            TreeNode temp = current.left;
            current.left = current.right;
            current.right = temp;

            if (current.left != null) {
                queue.offer(current.left);
            }
            if (current.right != null) {
                queue.offer(current.right);
            }
        }

        return root;
    }
}