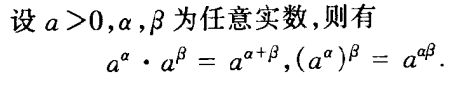数学分析(4): 函数的连续性

---

连续性的概念

为了引入函数连续性的多种定义，我们记△x为x的增量

|| 定义一：函数在一点上连续性定义（极限）
设函数f在某U(x0)内有定义，若lim_x–>x0f(x) = f(x0)，则称f在点x0处连续

|| 定义一的另一种形式：函数在一点上连续性定义（引入增量的极限）
设函数f在某U(x0)内有定义，若lim_△x–>0（△y） = 0，则称f在点x0处连续

|| 定义一的等价定义：函数在一点上连续性的ε - ∂定义
若对任给的ε>0，存在∂>0，使得当| x - x₀ | < ∂, 都有 | f(x) - f(x0) | < ε，则称f在点x0处连续
(注意与函数极限的定义中的区别： 以为x=x0是显然成立的，定义域不为空心领域，故转换为表达式时，有 | x - x₀ | < ∂，而非 0 < | x - x₀ | < ∂)

|| 极限与连续的关系：在x0连续其实就是在x0上的极限等于f(x0)。

|| f在x0无定义时，在x0可以极限，但是不可能有连续

|| 定义二：函数在一点上的左右连续
设函数在U⁺(x0) / U^-(x0) 内有定义，若满足：
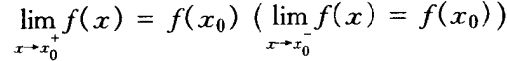，则称f在x0有右/左连续

|| 定理1：函数f在点x₀连续的充要条件是：f在x0即是左连续，又是右连续

|| 定义三：间断点的定义
设函数在U⁰（x0）内有定义，若满足任一个条件：

• f 在点x0无定义
• f 在x0极限不存在
• f 在点x0有定义但是不连续（lim_x–>x0f(x) != f(x0)）
  即可称点x0为间断点或不连续点

|| 间断点的分类：
第一类间断点(左右极限都存在)：可去间断点，跳跃间断点
第二类间断点(左右极限不都存在)

|| 可去间断点的定义：
若函数 f 满足下列任一条件：
- f 在x0有极限，但在点x0无定义
- f在点x0有定义，但是不连续（lim_x–>x0f(x) != f(x0) ）
则称其为可去间断点

|| 跳跃间断点的定义：
若函数f 在点x0的左右极限都存在，但左极限不等于右极限，则称点x0为函数f的跳跃间断点

|| 第二类间断点的定义：
至少一侧的极限不存在，即是第二类间断点

|| 定义四：区间上的连续函数
若函数f在区间 I 上的每一个点都连续，则称f为区间 I 上的连续函数。
对于闭区间或半开半闭区间的端点，函数在这些点上连续是指左连续或右连续

|| 若函数f在区间[a, b]上仅有有限个第一类间断点，那么称 f(x)在区间上分段连续

---

函数连续的性质

连续函数的局部性质
（注意：连续函数必有极限，所以函数连续的性质可以类比函数极限的性质）

|| 定理2： 局部有界性
若函数 f 在点x0处连续，则f在某U（x0）内有界

|| 定理3：局部保号性
若函数 f 在点x0来连续，且f(x0) > 0，则对任何正数r < f（x0），存在某U（x0），使得对一切x∈U（x0），有f(x) > r

|| 定理4：四则运算
若函数f和g在点x0连续，则f±g，f*g，f / g ( g(x0) != 0)都在x0连续

|| 定理5：复合函数的连续性
若函数f在x0连续，g在h0（h0 = f（x0) ）连续，则复合函数g 。f 在x0上也连续

闭区间上连续函数的整体性质

以下讨论设，函数f为闭区间 D [a, b]上的连续函数

|| 定义五：设f为定义在数集D上的连续函数，若存在x0∈D，使得对一切x∈D有f（x0） ≥f（x）
则称f在D上有最大值。

|| 定理6： 最大，最小值定理（连续区间中必有区间最值）
若函数在闭区间D上连续，则函数f在D上有最大最小值。

|| 定理6（推论）：有界性定理
若函数 f 在闭区间D上连续，则函数 f 在D上有界

|| 定理7：介值性定理
若函数 f 在闭区间[a, b]上连续，且f（a） != f（b），若u 是f（a），f（b）上的任一实数，满足f（a）> f ( u ) > f（b）或者f（b）> f ( u ) > f（a）。则至少存在一个点x0，使得f（x0） = u；

|| 定理7（推论）：根的存在性定理
若函数 f 在闭区间[a, b] 上连续，且f（a）f（b）< 0（即f(a)与f(b)异号），则至少存在一个点x0，使得f（x0）= 0（即至少有一个根）

反函数的连续性

|| 定理8：关于反函数连续性定理
若函数 f在[a，b]上严格单调并连续，则反函数在其定义域[f(a), f(b)] （或[f(b), f(a)]）上连续

一致连续性（一种更强的连续性。剔除虽连续但巨变的连续函数）

|| 定义六：一致连续性的定义（类似柯西准则）
设f 为定义在区间 I 上的函数，若对任给的ε>0，都存在∂ = ∂（ε）> 0，使得对于任一x1，x2∈ I，都有 | f（x1）- f（x2） | < ε，则称函数 f 在区间 I 上一致连续

|| 定理9：一致连续性定理
若函数是在闭区间上连续的，那么它在该闭区间一致连续

---

初等函数的连续性

已知基本初等函数中，三角函数，反三角函数以及有理指数幂都是连续函数
现在我们讨论指数函数，对数函数，和实指数幂函数的连续性

|| 定理10：指数函数的基本性质

|| 定理11：指数函数必连续
指数函数a^x （a > 0）在R上是连续的

|| 定理12：基本初等函数的连续性
一切的基本初等函数都是其定义域上的连续函数

|| 定理12（推论）：（因为初等函数都是由基本初等函数经过有限次的四则运算和复合操作得出的）
一切的初等函数都是其定义域内上的连续初等函数。