【数据结构】顺序表 | 详细讲解

在计算机中主要有两种基本的存储结构用于存放线性表：顺序存储结构和链式存储结构。本篇文章介绍采用顺序存储的结构实现线性表的存储。

顺序存储定义

线性表的顺序存储结构，指的是一段地址连续的存储单元依次存储链性表的数据元素。

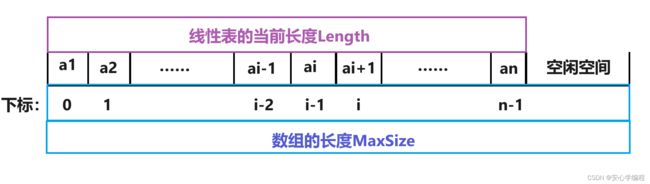
线性表的（，……）的顺序存储示意图如下：

就比如说，在大学期间，我们同宿舍的有一个同学，人特别老实、热心，我们时常会让他帮我们去图书馆占座，他总是答应，你想想，我们一个宿舍连他共有九个人，这其实明摆着是欺负人的事。他每次一吃完早饭就冲去图书馆，挑一个好地儿，把他的书包里的书，一本一本地按座位放好，若书包里的书不够，他会把他的饭盒、水杯、水笔都用上，长长一排，九个座位硬是被他给占了，后来有一次因占座的事情弄得差点都要打架。

顺序存储方式

线性表的顺序存储结构，说白了，和刚刚的例子一样，就是在内存中找了块地，通过占位的形式，把一定的内存空间给占了，然后把相同数据类型的数据元素依次存放在这块空地中。既然线性表的每个数据元素的类型都相同，所以可以用C语言（其他语言也相同）的一维数组来实现顺序存储结构，即把第一个数据元素存到数组下标为0的位置中，接着把线性表相邻的元素存储在数组中相邻的位置。

线性表中，我们估算这个线性表的最大存储容量，建立一个数组，数组的长度就是这个最大存储容量。随着数据的插入，我们线性表的长度开始变大，不过线性表的当前长度不能超过存储容量，即数组的长度。

数据长度与线性表长度区别

注意哦，这里有两个概念“数据的长度”和“线性表的长度”需要区分一下。

数组的长度是存放线性表的存储空间的长度，在静态分配的一维数组中，存储分配后这个量是一般不变的。但在动态分配的一维空间中，是可以实现动态分配数组。

线性表的长度是线性表中数据元素的个数，随着线性表插入和删除操作的进行，这个量是变化的。

地址计算方法

由于我们数数都是从1开始数的，线性表的定义也不能免俗，起始也是1，可C语言中的数组是从0开始的，于是线性表的第i个元素是要存储在数组下标为i-1的位置，即数据元素的序号和存放它的数组下标之间存在对应的关系。

用数组存储顺序表意味着要分配固定长度的数组空间，由于线性表中可以进行插入和删除操作，因此分配的数组空间要大于等于当前线性表的长度。

存储器中的每一个存储单元都有自己的编号，这个编号称为地址。在前一个地址确定好之后，那么后面的位置都是可以计算的。由于每个数据元素，不管它是整形、实型还是字符型， 它都是需要占用一定的存储单元空间的。假设占用的是c个存储单元，那么线性表中第i+1个数据元素的存储位置和第i个数据元素的存储位置满足下列关系（LOC表示获得存储位置的函数）。

LOC()=LOC()+c

所以对于第i个数据元素的存储位置可以由推算得出：

LOC()=LOC()+(i-1)*c

地址计算公式，可以随时算出线性表中任意位置的地址，不管它是第一个还是最后一个，都是相同的时间。那么我们对每个线性表位置的存入或者取出数据，对于计算机来说都是相等的时间，也就是一个常数，因此用我们算法中学到的时间复杂度的概念来说，它的存取时间性能为O(1)。具有这一特点的存储结构称为随机存取结构。

顺序表的代码实现分析

顺序表是用一段物理地址连续的存储单元依次存储数据元素的数据结构，一般情况下采用数组存储。在数组上完成数据的增删改查。

顺序表一般可以分为：

1. 静态顺序表：使用定长数组存储元素。
2. 动态顺序表：使用动态开辟的数组存储。

//顺序表的静态存储
#define N 7
typedef int SLDataType;
typedef struct SeqList
{
	SLDataType array[N];//定长数组
	size_t size;        //有效数据的个数
}SL;


//顺序表的动态存储
typedef int SLDataType;
typedef struct SeqList
{
	SLDataType* array; //指向动态开辟的数组
	size_t size;//有效数据个数
	size_t capacity;//容量空间的大小
}SL;

其实在平时以及以后的工作环境中，静态存储实践很少，因为不知道需要多少内存空间，N给大了不够用，N给小了浪费。静态顺序表只适合用于确定知道需要存多少数据的场景。所以在现实中基本都是使用动态顺序表，根据需要动态的分配空间大小，所以下面我们实现动态顺序表。

顺序表的结构代码

typedef int SLDataType;
//顺序表的动态存储
typedef struct SeqList
{
	SLDataType* a; //指向动态开辟的数组
	size_t size;//有效数据个数
	size_t capacity;//容量空间的大小
}SL;

顺序表的初始化

在这个顺序表中有一个a数组，一个size是指有效数据的个数，一个capacity是容量空间的大小。对于size而言，size是有效数据的个数，而看作下标的话，那便是最后一个元素的下一个下标。

在进行初始化是，要对数组以及顺序表结构体中的size以及capacity都进行初始化。

void SLInit(SL* psl)
{
	psl->a = NULL;
	psl->size = 0;
	psl->capacity = 0;
}

顺序表的销毁

起初，顺序表是一个空表，但是经过了一系列的增删改查之后就会存储一些数据，之后我们在销毁这个链表时，这个链表就是有内容的，所以在这里我们需要注意的是，销毁时需要断言一下这个顺序表是否为空，如果是空表的话，那还销毁什么。其次在销毁时，思路也很简单，无非就是让这个顺序表的几个变量都变为0。

void SLDestory(SL* psl)
{
	assert(psl);
	if (psl->a != NULL)
	{
		free(psl->a);
		psl->a = NULL;
		psl->size = 0;
		psl->capacity = 0;
	}
}

顺序表的遍历打印

遍历打印的思路极其类似于数组的打印，利用下标即可。下标是从零开始的，且size是有效数据的个数即最后一个数据的下一个下标，所以这里的循环条件就是i

void SeqListPrint(SL* psl)
{
	assert(psl);
	int i = 0;
	for (i = 0; i < psl->size; i++)
	{
		printf("%d ", psl->a[i]);
	}
	printf("\n");
}

顺序表的扩容 

因为在刚刚开始的时候，我们初始化size以及capacity都为0，所以为了防止每次扩容都是0，所以利用三目操作符来进行判断，如果这个capacity为0的话，那么就直接扩容4字节，其他的都是扩容它的两倍。

void SLCheckCapacity(SL* psl)
{
	assert(psl);
	int Newcapacity = psl->capacity == 0 ? 4 : psl->capacity * 2;
	SLDataType* tmp = (SLDataType*)realloc(psl->a, Newcapacity * sizeof(SLDataType));
	if (tmp == NULL)
	{
		perror("realloc fail\n");
	}
	psl->a = tmp;
	psl->capacity = Newcapacity;
}

顺序表的尾插

在添加数据时，不论是前插后插还是在指定位置插入，我们都需要为其判断是否有足够的空间，也就是判断是否需要扩容。扩容之后将数据插入顺序表中。

void SeqListPushBack(SL* psl, SLDataType x)
{
	assert(psl);
	SLCheckCapacity(psl);
	psl->a[psl->size - 1] = x;
	psl->size++;
}

这里注意一下，在尾插之后需要将size++。 

顺序表的头插

顺序表的头插相比较尾插就较难一些，因为需要将所有的数据都向后挪动一位。所以得再借助一个指针用来遍历。

void SeqListPushFront(SL* psl, SLDataType x)
{
	assert(psl);
	SLCheckCapacity(psl);
	int end = psl->size - 1;
	while (end >= 0)
	{
		psl->a[end+1] = psl->a[end];
		end--;
	}
	psl->a[0] = x;
	psl->size++;
}

顺序表的尾删

尾删还是比较容易的，无非就是将size--，但是这里还要断言一下确保size是大于零的。

void SeqListPopBack(SL* psl)
{
	assert(psl);
	assert(psl->size > 0);
	psl->size--;
}

顺序表的头删

如果想要头删的那话，就是将后面的元素给覆盖到前一个，从前往后开始。

void SeqListPopFront(SL* psl)
{
	assert(psl);
	assert(psl->size > 0);
	int begin = 1;
	while (begin <= psl->size - 1)
	{
		psl->a[begin - 1] = psl->a[begin];
		begin++;
	}
	psl->size--;
}

顺序表的查找

顺序表查找，在这个顺序表中是否有这个数组。其实这个也就是遍历，很简单利用下标。

int SeqListFind(SL* psl, SLDataType x)
{
	int i = 0;
	for (int i = 0; i < psl->size; i++)
	{
		if (psl->a[i] == x)
		{
			return i;
		}
	}
}

顺序表在pos位置插入x的数

这里我们需要断言一下这个是否为有效位置。 

void SeqListInsert(SL* psl, int pos, SLDataType x)
{
	assert(psl);
	assert(pos >= 0 && pos <= psl->size);
	SLCheckCapacity(psl);
	int end = psl->size - 1;
	while (end >= pos)
	{
		psl->a[end + 1] = psl->a[end];
		end--;
	}
	psl->a[pos] = x;
	psl->size++;
}

顺序表删除pos位置上的值

void SeqListErase(SL* psl, int pos)
{
	assert(psl);
	assert(pos >= 0 && pos <= psl->size);
	int begin = pos + 1;
	while (begin <= psl->size - 1)
	{
		psl->a[begin - 1] = psl->a[begin];
		begin++;
	}
	psl->size--;
}