【图像分类】【深度学习】【Pytorch版本】 GoogLeNet(InceptionV2)模型算法详解

【图像分类】【深度学习】【Pytorch版本】 GoogLeNet(InceptionV2)模型算法详解

---

前言

GoogLeNet(InceptionV2)是由谷歌的Ioffe, Sergey等人在《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift【ICML-2015】》【论文地址】一文中提出的带有Batch Normalization的改进模型，即在InceptionV1的基础上于卷积层与激活函数之间插入BN层，主要特点是使归一化(标准化)成为模型架构的一部分，并为每个训练小批量数据执行归一化。

---

GoogLeNet(InceptionV2)讲解

Internal Covariate Shift问题： 网络训练过程伴随着参数的更新，除了输入层的数据已经人为进行归一化以外，后面模型每一层的输入数据分布是会一直发生变化的，因为上一层参数的更新将导致下一层输入数据分布的变化。当每一层的输入数据分布发生变化时，后续层需要重新适应新的输入分布，增加了训练的复杂性。随着模型的深度增加，如果输入分布的变化很大，每层特征值分布会逐渐的向激活函数的输出区间的上下两端(激活函数饱和区间)靠近，长此以往网络可能会出现梯度消失或梯度爆炸的问题，从而无法继续训练模型。此外，由于每一层的输入分布变化不稳定不一致，网络很难收敛到最优解，可能会导致网络过拟合和网络训练缓慢。
为了改善卷积神经网络中的Internal Covariate Shift(ICS)效应，解决思路便是在卷积层与激活函数之间插入Batch Normalization(BN)层，Batch Normalization的来源于白化操作，白化(Whitening)是传统机器学习里面常用的一种规范化数据分布的方法，对图像提取特征之前对图像做白化操作，让输入数据具有相同的特征分布并去除特征之间的相关性，即输入数据变换成0均值、单位方差的正态分布。BN层的目的就是使输入到中间网络层的特征图满足均值为0，方差为1的分布规律。

Batch Normalization公式

BN层的计算通常是在卷积层之后，激活函数之前，对深层网络中间的特征值(或者叫隐藏值、中间值)进行标准化。在训练过程中，BN层的标准化均值和方差的计算依赖于当前batch的均值和方差，而不是整体数据的均值和方差，然后进行了变换重构，引入了可学习参数$\gamma$、$\beta$。
Batch Normalization的前向传播过程在训练和测试阶段有所不同。
训练阶段： BN层对每一批训练数据都进行归一化，即使用每一批数据各自的均值和方差，因此每一批数据的方差和标准差不同。Batch Normalization进行以下几个步骤：

1. 计算$m$个输入数据的均值：${\mu }_B\leftarrow \frac{1}{\mathrm{m}}{\Sigma }_{\mathrm{i}=1}^{\mathrm{m}}{x}_i$
2. 计算$m$个输入数据的方差：${\sigma }_B^2\leftarrow \frac{1}{\mathrm{m}}{\Sigma }_{\mathrm{i}=1}^{\mathrm{m}}{\left(x_i-{\mu }_B\right)}^2$
3. 对$m$个输入数据进行标准化(正太化)：$\stackrel{\wedge }{x_i}\leftarrow \frac{x_i-{\mu }_B}{\sqrt{{\sigma }_B^2+\epsilon }}$
4. 对$m$个输入数据进行尺度和偏差变换：$y_i=\gamma \stackrel{\wedge }{x_i}+\beta$

输入数据总共划分为$B$个批量，每个批量数据量为$m$个。

测试阶段： 一般只输入一个测试样本，使用的均值和方差是整个数据集训练后的均值和方差，通过滑动平均法计算而来。Batch Normalization进行以下几个步骤：

1. 计算输入数据的均值：$E\left[x\right]=E_B\left[{\mu }_B\right]$
2. 计算输入数据的方差：$Var\left[x\right]=\frac{\mathrm{m}}{\mathrm{m}-1}{E}_B\left[{\sigma }_B^2\right]$
3. 对输入数据进行尺度和偏差变换：$y=\frac{\gamma }{\sqrt{Var\left[x\right]+\epsilon }}x+\left(\beta -\frac{\gamma E\left[x\right]}{\sqrt{Var\left[x\right]+\epsilon }}\right)$

Batch Normalization的反向传播
这部分看不懂问题也不大，博主也是花了半天才弄懂的，只是一堆求导

$\ell$是损失值loss

1.$\stackrel{\wedge }{x_i}$的梯度:$$\frac{\partial \ell }{\partial \stackrel{\wedge }{x_i}}=\frac{\partial \ell }{\partial {\mathrm{y}}_i}\cdot \frac{\partial {\mathrm{y}}_i}{\partial {\mathrm{x}}_i}=\frac{\partial \ell }{\partial {\mathrm{y}}_i}\cdot \gamma$$
2.${\sigma }_B^2$的梯度:$$\frac{\partial \ell }{\partial {\sigma }_B^2}=\{\begin{array}{c}{\sum }_{\mathrm{i}=1}^{\mathrm{m}}\frac{\partial \ell }{\partial \stackrel{\wedge }{x_i}}\frac{\partial \stackrel{\wedge }{x_i}}{\partial {\sigma }_B^2}\\ \frac{\partial \stackrel{\wedge }{x_i}}{\partial {\sigma }_B^2}=\left(x_i-{\mu }_B\right)\frac{-1}{2}{\left({\sigma }_B^2+\epsilon \right)}^{\frac{-3}{2}}\end{array}=\sum _{\mathrm{i}=1}^{\mathrm{m}}\frac{\partial \ell }{\partial \stackrel{\wedge }{x_i}}\cdot \left(x_i-{\mu }_B\right)\frac{-1}{2}{\left({\sigma }_B^2+\epsilon \right)}^{\frac{-3}{2}}$$
3.${\mu }_B$的梯度:$$\frac{\partial \ell }{\partial {\mu }_B}=\{\begin{array}{c}{\sum }_{\mathrm{i}=1}^{\mathrm{m}}\frac{\partial \ell }{\partial \stackrel{\wedge }{x_i}}\frac{\partial \stackrel{\wedge }{x_i}}{\partial {\mu }_B}+\frac{\partial \ell }{\partial {\sigma }_B^2}\frac{\partial {\sigma }_B^2}{\partial {\mu }_B}\\ \frac{\partial \stackrel{\wedge }{x_i}}{\partial {\mu }_B}=\frac{-1}{\sqrt{{\sigma }_B^2+\epsilon }}\\ \frac{\partial {\sigma }_B^2}{\partial {\mu }_B}={\sum }_{\mathrm{i}=1}^{\mathrm{m}}\frac{-2\left(x_i-{\mu }_B\right)}{m}\end{array}=\sum _{\mathrm{i}=1}^{\mathrm{m}}\frac{\partial \ell }{\partial \stackrel{\wedge }{x_i}}\cdot \frac{-1}{\sqrt{{\sigma }_B^2+\epsilon }}+\frac{\partial \ell }{\partial {\sigma }_B^2}\cdot \sum _{\mathrm{i}=1}^{\mathrm{m}}\frac{-2\left(x_i-{\mu }_B\right)}{m}$$
4.$x_i$的梯度:$$\frac{\partial \ell }{\partial x_i}=\{\begin{array}{c}\frac{\partial \ell }{\partial \stackrel{\wedge }{x_i}}\frac{\partial \stackrel{\wedge }{x_i}}{\partial x_i}+\frac{\partial \ell }{{\sigma }_B^2}\frac{{\sigma }_B^2}{\partial x_i}+\frac{\partial \ell }{\partial {\mu }_B}\frac{\partial {\mu }_B}{\partial x_i}\\ \frac{\partial \stackrel{\wedge }{x_i}}{\partial x_i}=\frac{1}{\sqrt{{\sigma }_B^2+\epsilon }}\\ \frac{{\sigma }_B^2}{\partial x_i}=\frac{2}{m}\left(x_i-{\mu }_B\right)\left(1-\frac{1}{m}\right)+\frac{2}{m}{\sum }_{\mathrm{k}=1,k!=i}^{\mathrm{m}}\left(x_{\mathrm{k}}-{\mu }_B\right)\left(-\frac{1}{m}\right)=\frac{2}{m}\left(x_i-{\mu }_B\right)+\frac{2}{m}{\sum }_{\mathrm{k}=1}^{\mathrm{m}}\left(x_{\mathrm{k}}-{\mu }_B\right)\left(-\frac{1}{m}\right)=\frac{2}{m}\left(x_i-{\mu }_B\right)+0\\ \frac{\partial {\mu }_B}{\partial x_i}=\frac{1}{m}\end{array}=\frac{\partial \ell }{\partial \stackrel{\wedge }{x_i}}\cdot \frac{1}{\sqrt{{\sigma }_B^2+\epsilon }}+\frac{\partial \ell }{{\sigma }_B^2}\cdot \frac{2}{m}\left(x_i-{\mu }_B\right)+\frac{\partial \ell }{\partial {\mu }_B}\frac{1}{m}$$
5.$\gamma$的梯度:$$\frac{\partial \ell }{\partial \gamma }=\sum _{\mathrm{i}=1}^{\mathrm{m}}\frac{\partial \ell }{\partial {\mathrm{y}}_i}\cdot \stackrel{\wedge }{x_i}$$
6.$\beta$的梯度:$$\frac{\partial \ell }{\partial \beta }=\sum _{\mathrm{i}=1}^{\mathrm{m}}\frac{\partial \ell }{\partial {\mathrm{y}}_i}$$

InceptionV2结构

在VggNet中就提出了用小卷积核替代大卷积核，在保持感受野范围一致的前提下又减少了参数量。VggNet中通过堆叠俩个3×3的卷积核可以等效替代一个5×5的卷积核，堆叠三个3×3的卷积核可以等效替代一个7×7的卷积核，InceptionV2借鉴了这种思想将InceptionV1结构中的5×5卷积核替换为2个3×3卷积核。

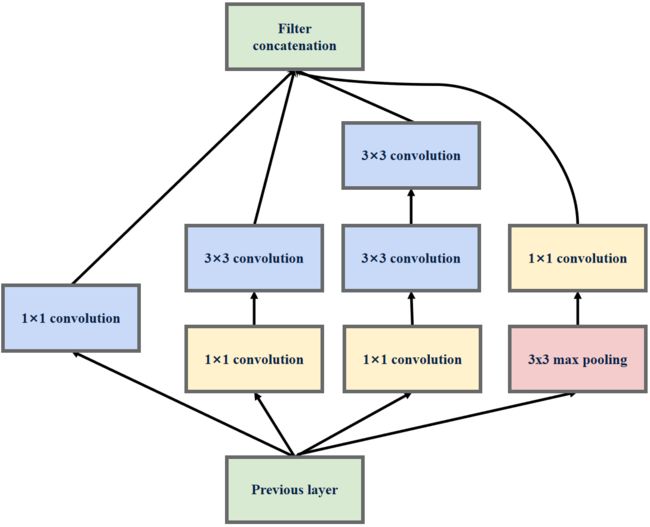
InceptionV2特殊结构

在中间层中，出现了部分特殊的InceptionV2结构，该结构舍弃了1×1卷积层分支，而在池化分支部分同样舍弃了1×1卷积层，并且该结构的输出特征图的尺寸会缩小为输入特征图尺寸的一半。

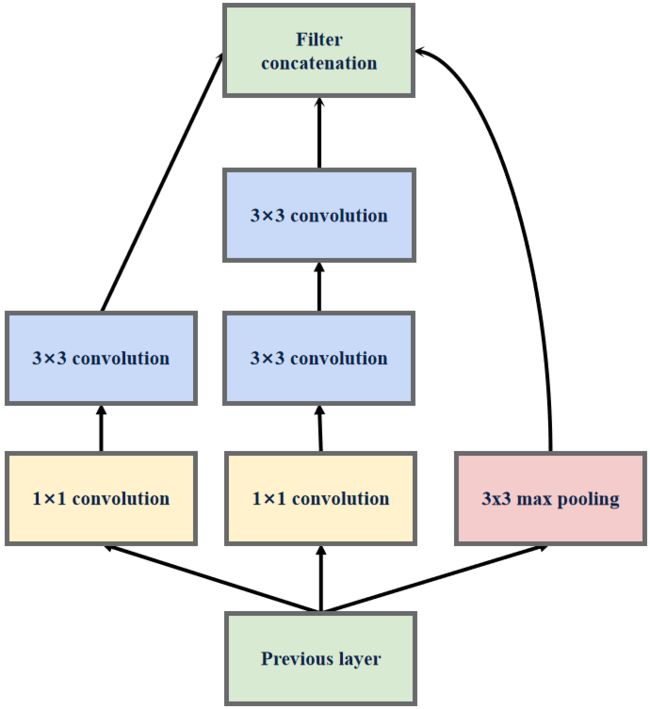
GoogLeNet(InceptionV2)模型结构

下图是原论文给出的关于 GoogLeNet(InceptionV2)模型结构的详细示意图：

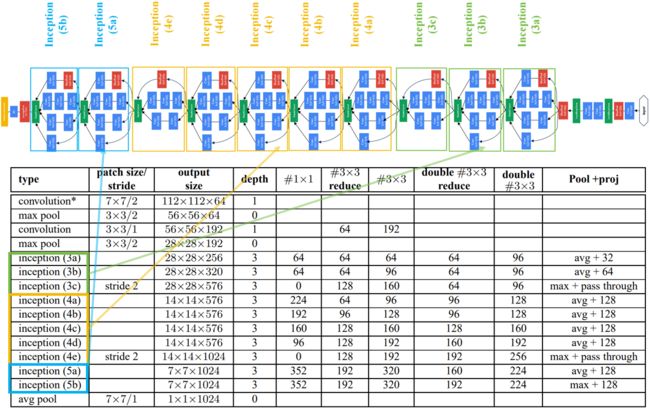
GoogLeNet(InceptionV2)模型舍弃了辅助分类器分支。
GoogLeNet在图像分类中分为两部分：backbone部分： 主要由InceptionV2模块、卷积层和池化层(汇聚层)组成，分类器部分： 由全连接层组成。

读者注意了,原始论文标注的通道数有一部分是错的，写代码时候对应不上。

博主仿造GoogLeNet(InceptionV1)的结构绘制了以下GoogLeNet(InceptionV2)的结构。

---

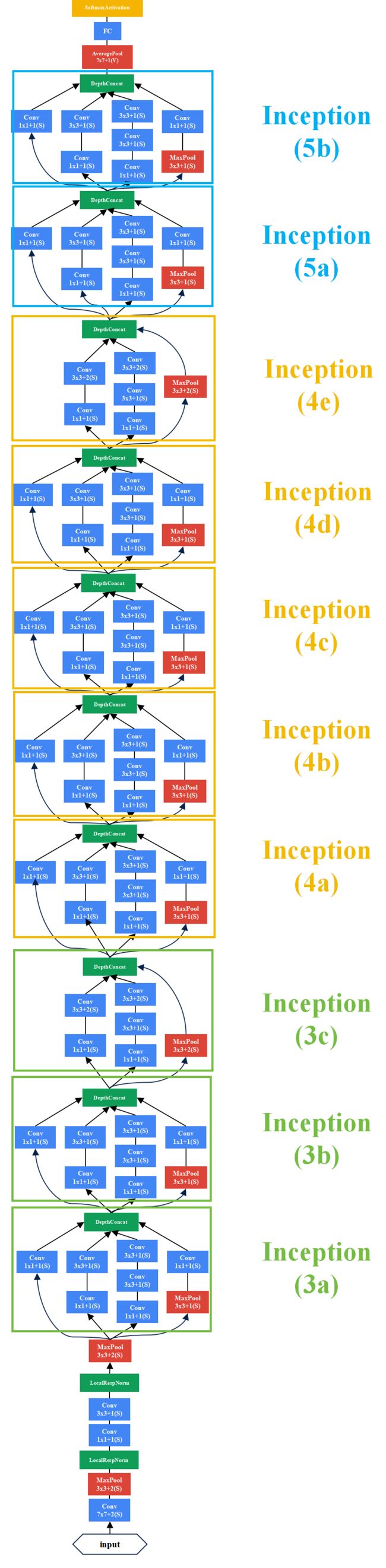
GoogLeNet(InceptionV2) Pytorch代码

卷积层组： 卷积层+BN层+激活函数

# 卷积组: Conv2d+BN+ReLU
class BasicConv2d(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
        super(BasicConv2d, self).__init__()
        self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding)
        self.bn = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)
    def forward(self, x):
        x = self.conv(x)
        x = self.bn(x)
        x = self.relu(x)
        return x

InceptionV1模块： 卷积层组+池化层

# InceptionV2:BasicConv2d+MaxPool2d
class InceptionV2A(nn.Module):
    def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch3x3redX2, ch3x3X2, pool_proj):
        super(InceptionV2A, self).__init__()
        # 1×1卷积
        self.branch1 = BasicConv2d(in_channels, ch1x1, kernel_size=1)
        # 1×1卷积+3×3卷积
        self.branch2 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3red, kernel_size=1),
            BasicConv2d(ch3x3red, ch3x3, kernel_size=3, padding=1)   # 保证输出大小等于输入大小
        )
        # 1×1卷积++3×3卷积+3×3卷积
        self.branch3 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3redX2, kernel_size=1),
            BasicConv2d(ch3x3redX2, ch3x3X2, kernel_size=3, padding=1),
            BasicConv2d(ch3x3X2, ch3x3X2, kernel_size=3, padding=1)         # 保证输出大小等于输入大小
        )
        # 3×3池化+1×1卷积
        self.branch4 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            BasicConv2d(in_channels, pool_proj, kernel_size=1)
        )
    def forward(self, x):
        branch1 = self.branch1(x)
        branch2 = self.branch2(x)
        branch3 = self.branch3(x)
        branch4 = self.branch4(x)
        # 拼接
        outputs = [branch1, branch2, branch3, branch4]
        return torch.cat(outputs, 1)

InceptionV1特殊模块(三分支)： 卷积层组+池化层

# InceptionV2:BasicConv2d+MaxPool2d
class InceptionV2B(nn.Module):
    def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch3x3redX2, ch3x3X2, pool_proj):
        super(InceptionV2B, self).__init__()
        # ch1x1:没有1×1卷积
        # 1×1卷积+3×3卷积,步长为2
        self.branch1 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3red, kernel_size=1),
            BasicConv2d(ch3x3red, ch3x3, kernel_size=3, stride=2, padding=1)   # 保证输出大小等于输入大小
        )
        # 1×1卷积+3×3卷积+3×3卷积,步长为2
        self.branch2 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3redX2, kernel_size=1),
            BasicConv2d(ch3x3redX2, ch3x3X2, kernel_size=3, padding=1),   # 保证输出大小等于输入大小
            BasicConv2d(ch3x3X2, ch3x3X2, kernel_size=3, stride=2, padding=1)         # 保证输出大小等于输入大小
        )
        # 3×3池化,步长为2
        self.branch3 = nn.Sequential(nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
        # pool_proj:池化层后不再接卷积层

---

完整代码

import torch.nn as nn
import torch
import torch.nn.functional as F
from torchsummary import summary

class GoogLeNetV2(nn.Module):
    def __init__(self, num_classes=1000, aux_logits=True, init_weights=False):
        super(GoogLeNetV2, self).__init__()
        self.aux_logits = aux_logits

        self.conv1 = BasicConv2d(3, 64, kernel_size=7, stride=2, padding=3)
        self.maxpool1 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
        self.conv2 = BasicConv2d(64, 64, kernel_size=1)
        self.conv3 = BasicConv2d(64, 192, kernel_size=3, padding=1)
        self.maxpool2 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.inception3a = InceptionV2A(192, 64, 64, 64, 64, 96, 32)
        self.inception3b = InceptionV2A(256, 64, 64, 96, 64, 96, 64)
        self.inception3c = InceptionV2B(320, 0, 128, 160, 64, 96, 0)

        self.inception4a = InceptionV2A(576, 224, 64, 96, 96, 128, 128)
        self.inception4b = InceptionV2A(576, 192, 96, 128, 96, 128, 128)
        self.inception4c = InceptionV2A(576, 160, 128, 160, 128, 128, 128)
        self.inception4d = InceptionV2A(576, 96, 128, 192, 160, 160, 128)
        self.inception4e = InceptionV2B(576, 0, 128, 192, 192, 256, 0)

        self.inception5a = InceptionV2A(1024, 352, 192, 320, 160, 224, 128)
        self.inception5b = InceptionV2A(1024, 352, 192, 320, 160, 224, 128)

        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
        self.dropout = nn.Dropout(0.4)
        self.fc = nn.Linear(1024, num_classes)
        if init_weights:
            self._initialize_weights()

    def forward(self, x):
        # N x 3 x 224 x 224
        x = self.conv1(x)
        # N x 64 x 112 x 112
        x = self.maxpool1(x)
        # N x 64 x 56 x 56
        x = self.conv2(x)
        # N x 64 x 56 x 56
        x = self.conv3(x)
        # N x 192 x 56 x 56
        x = self.maxpool2(x)

        # N x 192 x 28 x 28
        x = self.inception3a(x)
        # N x 256 x 28 x 28
        x = self.inception3b(x)
        # N x 480 x 28 x 28
        x = self.inception3c(x)
        # N x 480 x 14 x 14
        x = self.inception4a(x)
        # N x 512 x 14 x 14
        x = self.inception4b(x)
        # N x 512 x 14 x 14
        x = self.inception4c(x)
        # N x 512 x 14 x 14
        x = self.inception4d(x)
        # N x 512 x 14 x 14
        x = self.inception4e(x)
        # N x 832 x 7 x 7
        x = self.inception5a(x)
        # N x 832 x 7 x 7
        x = self.inception5b(x)
        # N x 1024 x 7 x 7
        x = self.avgpool(x)
        # N x 1024 x 1 x 1
        x = torch.flatten(x, 1)
        # N x 1024
        x = self.dropout(x)
        x = self.fc(x)
        # N x 1000(num_classes)
        return x
    # 对模型的权重进行初始化操作
    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight, 0, 0.01)
                nn.init.constant_(m.bias, 0)

# InceptionV2:BasicConv2d+MaxPool2d
class InceptionV2A(nn.Module):
    def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch3x3redX2, ch3x3X2, pool_proj):
        super(InceptionV2A, self).__init__()
        # 1×1卷积
        self.branch1 = BasicConv2d(in_channels, ch1x1, kernel_size=1)
        # 1×1卷积+3×3卷积
        self.branch2 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3red, kernel_size=1),
            BasicConv2d(ch3x3red, ch3x3, kernel_size=3, padding=1)   # 保证输出大小等于输入大小
        )
        # 1×1卷积++3×3卷积+3×3卷积
        self.branch3 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3redX2, kernel_size=1),
            BasicConv2d(ch3x3redX2, ch3x3X2, kernel_size=3, padding=1),
            BasicConv2d(ch3x3X2, ch3x3X2, kernel_size=3, padding=1)         # 保证输出大小等于输入大小
        )
        # 3×3池化+1×1卷积
        self.branch4 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            BasicConv2d(in_channels, pool_proj, kernel_size=1)
        )
    def forward(self, x):
        branch1 = self.branch1(x)
        branch2 = self.branch2(x)
        branch3 = self.branch3(x)
        branch4 = self.branch4(x)
        # 拼接
        outputs = [branch1, branch2, branch3, branch4]
        return torch.cat(outputs, 1)

# InceptionV2:BasicConv2d+MaxPool2d
class InceptionV2B(nn.Module):
    def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch3x3redX2, ch3x3X2, pool_proj):
        super(InceptionV2B, self).__init__()
        # ch1x1:没有1×1卷积
        # 1×1卷积+3×3卷积,步长为2
        self.branch1 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3red, kernel_size=1),
            BasicConv2d(ch3x3red, ch3x3, kernel_size=3, stride=2, padding=1)   # 保证输出大小等于输入大小
        )
        # 1×1卷积+3×3卷积+3×3卷积,步长为2
        self.branch2 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3redX2, kernel_size=1),
            BasicConv2d(ch3x3redX2, ch3x3X2, kernel_size=3, padding=1),   # 保证输出大小等于输入大小
            BasicConv2d(ch3x3X2, ch3x3X2, kernel_size=3, stride=2, padding=1)         # 保证输出大小等于输入大小
        )
        # 3×3池化,步长为2
        self.branch3 = nn.Sequential(nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
        # pool_proj:池化层后不再接卷积层

    def forward(self, x):
        branch1 = self.branch1(x)
        branch2 = self.branch2(x)
        branch3 = self.branch3(x)
        # 拼接
        outputs = [branch1,branch2, branch3]
        return torch.cat(outputs, 1)

# 卷积组: Conv2d+BN+ReLU
class BasicConv2d(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
        super(BasicConv2d, self).__init__()
        self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding)
        self.bn = nn.BatchNorm2d(out_channels)
        self.relu = nn.ReLU(inplace=True)
    def forward(self, x):
        x = self.conv(x)
        x = self.bn(x)
        x = self.relu(x)
        return x

if __name__ == '__main__':
    device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
    model = GoogLeNetV2().to(device)
    summary(model, input_size=(3, 224, 224))

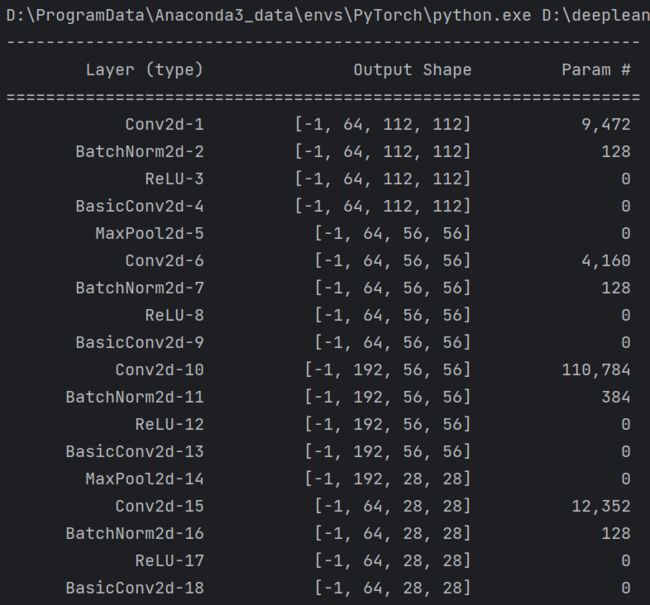
summary可以打印网络结构和参数，方便查看搭建好的网络结构。

---

总结

尽可能简单、详细的介绍了深度可分卷积的原理和卷积过程，讲解了GoogLeNet(InceptionV2)模型的结构和pytorch代码。