数据结构4：双向链表+OJ题

目录

双向链表的创建

 双向链表的结构体定义：

双向链表的头节点创建：

双向链表节点的创建：

双向链表的打印：

双向链表的尾插

双向链表的尾删

 双向链表头插

双向链表查找

 双向链表在pos的前面进行插入

双向链表删除pos位置的节点

链表OJ题

链表分割

链表的回文结构

相交链表

环形链表1

环形链表2

复制带随机指针的链表

---

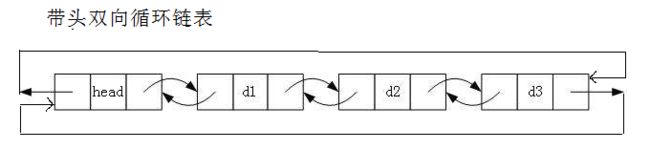
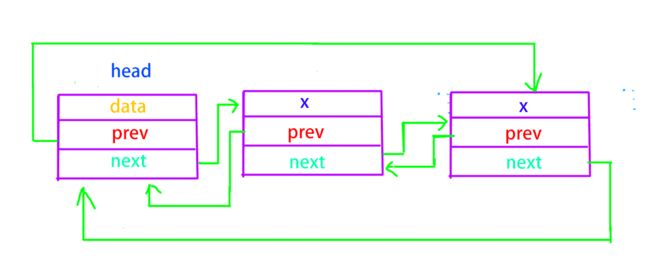
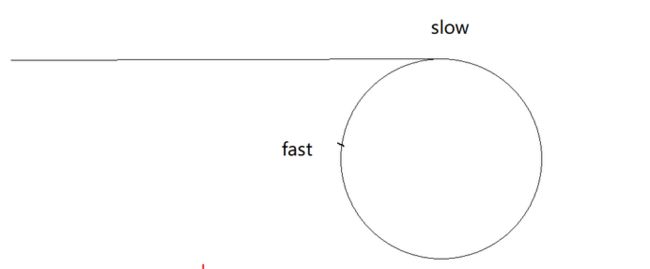
 双向循环链表其实很像一款小游戏：

 不陌生吧？循环的逻辑其实和双箭头的走到尽头回到开始处的效果是一样的。

 双向链表的逻辑结构是如上图所示的，看上去比单向链表复杂多了，不过正是因为它复杂的结构体，反而更方便我们去处理一些其中的细节。

双向链表的创建

 增删查改的接口：

ListNode* creatspace(DataType x);


// 创建返回链表的头结点.

ListNode* ListCreate();

// 双向链表销毁

void ListDestory(ListNode* phead);

// 双向链表打印

void ListPrint(ListNode* phead);

// 双向链表尾插

void ListPushBack(ListNode* phead, DataType x);

// 双向链表尾删

void ListPopBack(ListNode* phead);

// 双向链表头插

void ListPushFront(ListNode* phead, DataType x);

// 双向链表头删

void ListPopFront(ListNode* phead);

// 双向链表查找

ListNode* ListFind(ListNode* phead, DataType x);

// 双向链表在pos的前面进行插入

void ListInsert(ListNode* pos, DataType x);

// 双向链表删除pos位置的节点

void ListErase(ListNode* pos);

 双向链表的结构体定义：

typedef struct ListNode
{
	DataType data;

	struct ListNode* prev;//指向前一个节点
	struct ListNode* next;//指向后一个节点

}ListNode;

双向链表的头节点创建：

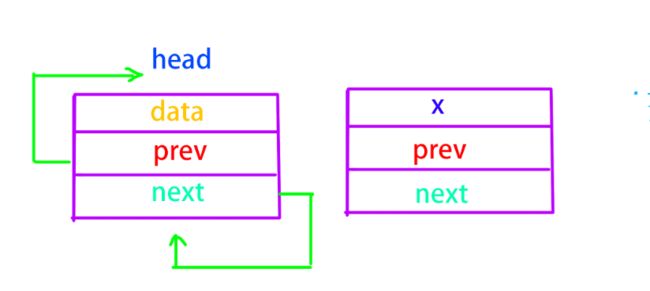
和单向链表相同，创建一个节点然后将其链接好，不过双向链表头子的结构要稍微复杂一点，为了实现循环，它的前指针和后指针都需要指向它自己。

头节点不需要存放数值

// 创建返回链表的头结点.

ListNode* ListCreate()
{
	ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
	if (newnode == NULL)
	{
		printf("malloc fail");
		exit(-1);
	}

	newnode->prev = newnode;
	newnode->next = newnode;
	return newnode;
}

---

双向链表节点的创建：

ListNode* Creatspace(DataType x)
{
	ListNode* newnode = (ListNode*)malloc(sizeof(ListNode));
	if (newnode == NULL)
	{
		printf ("malloc fail");
		exit(-1);
	}

	newnode->data = x;
	newnode->prev = NULL;
	newnode->next = NULL;

	return newnode;
}

逻辑和单向链表的节点是一样的，开辟新空间，存放入值，返回一个结构体指针。

---

双向链表的打印：

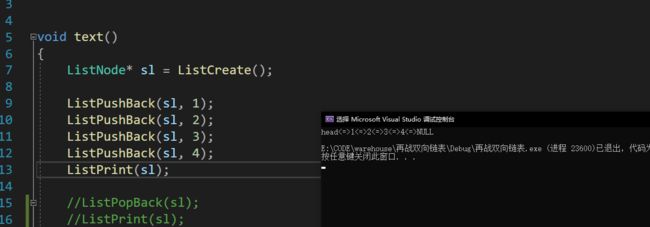
 打印循环的终止因为循环的原因，我们不能再将NULL当成链表结束的标志，不过头节点的作用就体现出来了，只需要循环到头指针停下来就好，为了让循环成功进入，cur不再初始化为phead，而是phead的next。

// 双向链表打印

void ListPrint(ListNode* phead)
{
	if(phead != NULL)
		printf("head<=>");


	ListNode* cur = phead->next;

	while (cur != phead)
	{
		printf("%d<=>", cur->data);
		cur = cur->next;
	}

	printf("NULL\n");
}

---

双向链表的尾插

 尾插时，创建节点，新节点与前节点向链接，也就是前节点的next指向新节点，新节点的prev指向前节点，而尾插的新节点的next则必定是头节点。

尾插相较于单向链表则方便得多，由于循环的存在，我们不需要遍历整个链表才能找到尾部节点

// 双向链表尾插

void ListPushBack(ListNode* phead, DataType x)
{
	
	assert(phead);

	ListNode* newnode = Creatspace(x);

	ListNode* prev = phead->prev;

	prev->next = newnode;
	newnode->prev = prev;
	newnode->next = phead;
	phead->prev = newnode;

}

---

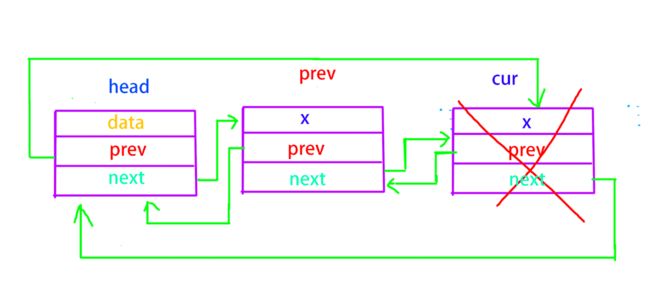
双向链表的尾删

 创建一个工具人指针，当删去尾部节点的时候再将新的尾部节点链接到头节点处。

// 双向链表尾删

void ListPopBack(ListNode* phead)
{
	assert(phead);

	ListNode* cur  = phead->prev;
	ListNode* prev = cur->prev;

	free(cur);
	cur = NULL;

	prev->next = phead;
	phead->prev = prev;


}

---

 双向链表头插

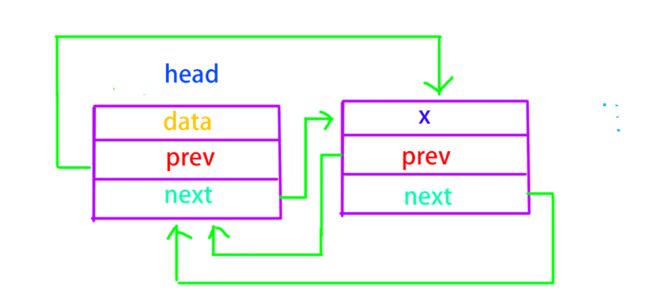
 头插的逻辑相当简单，直接在头节点后面插入就好了

// 双向链表头插

void ListPushFront(ListNode* phead, DataType x)
{
	assert(phead);

	ListNode* newnode = Creatspace(x);

	newnode->next = phead->next;
	newnode->prev = phead;
	phead->next->prev = newnode;
	phead->next = newnode;


}

---

双向链表查找

 依旧是遍历整个链表，找不到就直接返回NULL

// 双向链表查找

ListNode* ListFind(ListNode* phead, DataType x)
{
	assert(phead);

	ListNode* cur = phead->next;

	while (cur != phead)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}


	return NULL;
}

---

 双向链表在pos的前面进行插入

 配合前面的查找就可以实现插入

// 双向链表在pos的前面进行插入

void ListInsert(ListNode* pos, DataType x)
{

	ListNode* prev = pos->prev;

	ListNode* newnode = Creatspace(x);

	prev->next = newnode;
	newnode->prev = newnode;

	newnode->next = pos;
	pos->prev = newnode;


}

---

双向链表删除pos位置的节点

// 双向链表删除pos位置的节点

void ListErase(ListNode* pos)
{
	ListNode* prev = pos->prev;
	prev->next = pos->next;
	pos->next->prev = prev;

	free(pos);
	pos = NULL;

}

---

这样，一个实现了基本增删查改功能的双向链表就成功的被创建好了。

链表OJ题

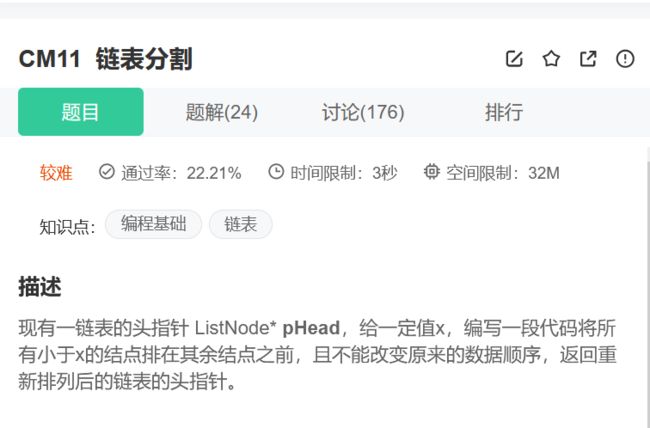
链表分割

 链接：链表分割_牛客题霸_牛客网

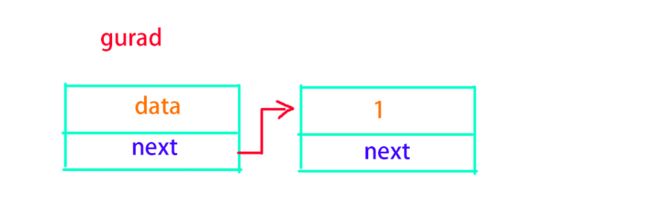
 这道题其实具体分析过后就会变得非常容易，不过在做这道题之前我们先抛出一个新概念，哨兵位节点。

其实就是双向链表的头节点，它不存放数据，永远指向第一个数据，只有销毁整个链表的时候才顺带销毁。所以在这里哨兵位指的就是一个不存放数据，始终指向第一个存放数据节点的一个单项链表节点。

 定义一个这样的哨兵位的好处非常多，首先就是免去了使用二级指针的问题，因为我们不需要再更改pHead这个指针所指向的节点，只需要更改哨兵位的next即可，而且寻找头节点将会变得更加容易，也不会有丢失头节点位置这种问题的情况发生。

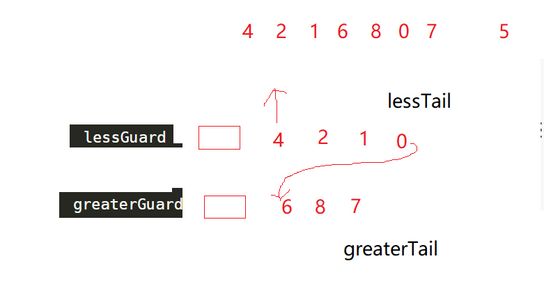
为什么在这里引入哨兵位的概念？因为题目要求我们不能改变原先的链表顺序，如果单纯的取小头插，取大尾插，我们会改变整个原先顺序。那么为了避免这个问题的发生，我们可以创建两个链表分开存储大于x的值和小于x的值，然后将其链接起来。

 哨兵位的存在就可以很方便的让我们找到头节点。

根据大体的逻辑，我们可以写出来这样的代码：

class Partition {
  public:
    ListNode* partition(ListNode* pHead, int x) {
        // write code here
        struct ListNode* BigGuard,*Bigcur,*SmallGurad,*Smallcur;
        BigGuard = Bigcur = (struct ListNode*)malloc (sizeof(struct ListNode));
        SmallGurad = Smallcur = (struct ListNode*)malloc (sizeof(struct ListNode));


        struct ListNode* cur = pHead;

        while (cur)
        {
            if(cur -> val >= x)
            {
                Bigcur->next  = cur;
                Bigcur = Bigcur->next;
            }
            else
            {
                Smallcur->next = cur;
                Smallcur = Smallcur->next;
            }
            cur = cur ->next;
        }

        Smallcur->next = BigGuard->next;



        free(BigGuard);
        free(SmallGurad);

        pHead =SmallGurad->next;
        return pHead;
   }
};

但是这样子是过不了的，为什么？

我们还需要考虑如下三种极端情况：

 首先是空链表问题，假如说传入了一个空链表，我们在链接大小的链表的时候就会出现问题

 Smallcur->next = BigGuard->next;

 while的条件是cur不为空，此时while没进去，这几个哨兵位的next都没有初始化，就都是随机值了。

为了防止这种情况，我们还要加上初始化。

  //空链表进不去while，以免产生随机值
        BigGuard->next = NULL；
        SmallGurad -> next = NULL;

当然还有大链表最后一个节点的next指向的不为空的问题，我们只需要在链接两个链表之间将bigcur的next置空即可。

        Smallcur->next = BigGuard->next;
        Bigcur ->next = NULL;

---

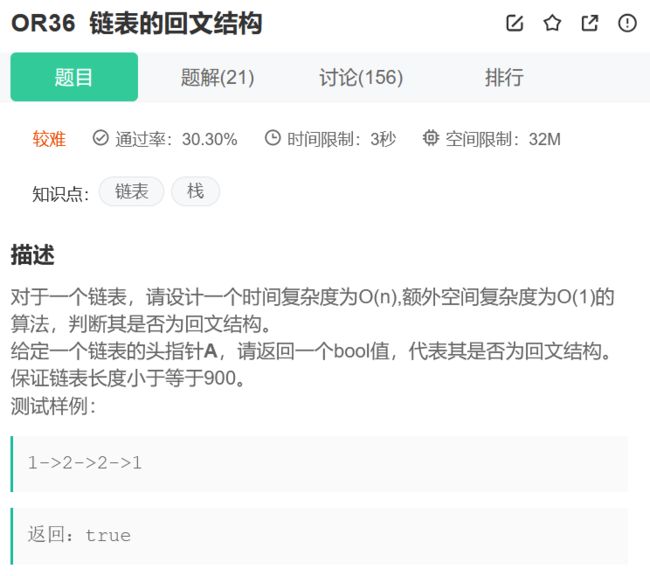
链表的回文结构

链接：链表的回文结构_牛客题霸_牛客网

 这道题需要处理奇数和偶数的情况，可能看上去比较复杂，但是我们可以充分利用我们前面写过的题目让这道题变得简单起来。

我们最基本的逻辑就是：找到中间节点，逆置中间节点后面的节点，从中间节点开始从头比较。

那么我们前面写过的链表逆置和寻找中间节点的题目答案都可以再拿过来用了。

class PalindromeList {
  public:

    struct ListNode* reverseList(struct ListNode* head) {

        struct ListNode* cur =  head;
        struct ListNode* next = NULL;
        struct ListNode* newhead = NULL;

        while (cur) {
            next = cur->next;

            cur -> next = newhead;
            newhead = cur ;
            cur = next;

        }
        return newhead;

    }
    struct ListNode* middleNode(struct ListNode* head) {
        struct ListNode* slow = head;
        struct ListNode* fast = head;

        while (fast && fast->next) {
            fast = fast->next->next;
            slow = slow->next;
        }

        return slow;
    }

    bool chkPalindrome(ListNode* A) {
        // write code here
      ListNode* mid =   middleNode(A);
      ListNode* rmid =  reverseList(mid);

      while (A && rmid)
      {

          if(A->val != rmid->val )
          {
            return false;
          }
        A=A->next;
        rmid = rmid ->next;
      }
       return true;
    }
};

头指针和中间节点指针只需要其中一个是空的时候就循环结束，这样子的话无论是奇数还是偶数都可以不用去特意判断，因为当整个链表为奇数的时候，由于逆置的巧合，头指针将不会指向中间节点而是指向空，这个时候无论如何整个链表比较的个数都是相等的。

 

---

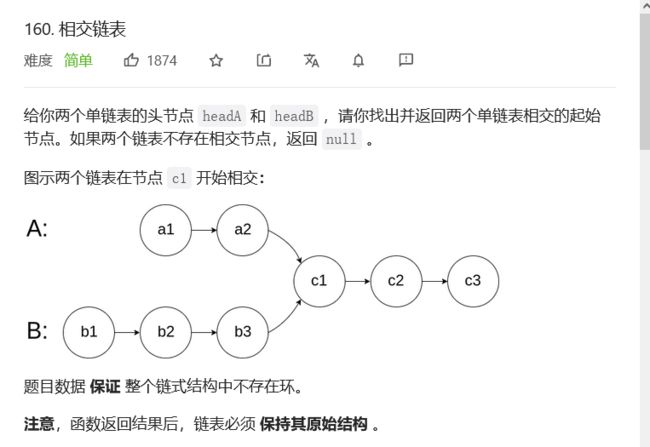
相交链表

 链接：力扣

 这题有两种解题思路：

 我们就用第二种方法求解：

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {


        struct ListNode * cura = headA;
        struct ListNode * curb = headB;

        int count1 = 0;
        int count2 = 0;

        while(cura)
        {
            cura = cura->next;
            ++count1;
        }
        while(curb)
        {
            curb = curb->next;
            ++count2;
        }
        if(cura != curb)
        {
            return NULL;
        }
        int n =abs(count1-count2);

        if(count1next;
            }
        }
        else 
        {
            while(n--)
            {
                headA = headA->next;
            }
        }
        while(headA)
        {
            if(headA != headB)
            {
            headA= headA->next;
            headB= headB->next;
            }
            else
            {
                return  headA;
            }
        }
        return NULL;
}

---

环形链表1

链接：力扣

 

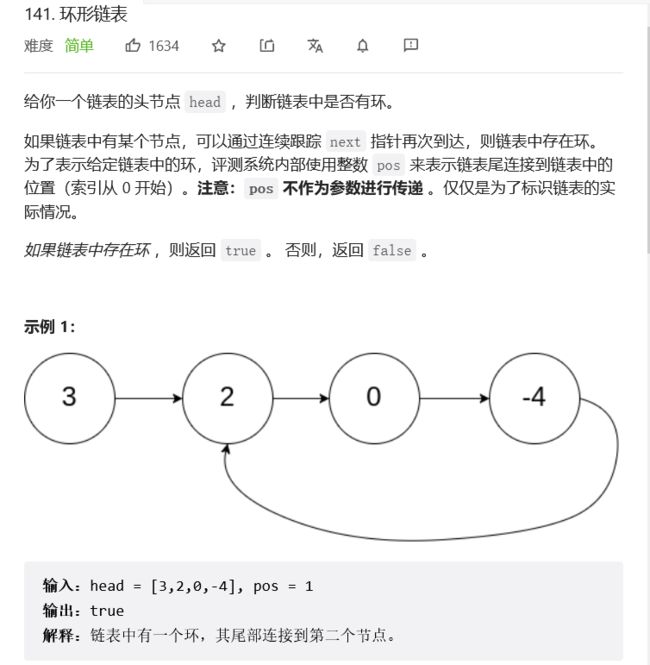
这道题可以用快慢指针，即慢指针一次走一步，快指针一次走两步，两个指针从链表其实位置开始运行，如果链表带环则一定会在环中相遇，否则快指针率先走到链表的末尾。
 

bool hasCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;

    while(fast && fast->next )
    {
        fast = fast->next->next;
        slow = slow->next;

        if(fast == slow)
        {
            return true;
        }
    }

    return false;

}

---

环形链表2

 链接：力扣

 这道题的代码还算是比较简单的，先说结论，照着结论写并不困难，难以理解的则是结论的推导。

结论：让一个指针从链表起始位置开始遍历链表，同时让一个指针从判环时相遇点的位置开始绕环
运行，两个指针都是每次均走一步，最终肯定会在入口点的位置相遇。

推导过程：

我们先假定有一个足够大的链表，其中有一个足够大的环

我们创建两个指针，一个为slow另一个为fast，slow的步长为1，fast为其两倍。

假设进环前的长度是L

环长C

入口到相遇点的距离为X

假定在slow进环前，fast已经在环内转了N圈 ，N>=1

A为链表起点

 那么fast走的距离为：X + L +N*C

 slow的为：L + X

那么当两个指针所走距离相等的时候，就是相遇点

由此列出表达式：2(L+X) = X + L +N*C

那么：                  L + X   = N * C

                                     L = N*C - X

表达式转化为语言描述即为结论：一个指针从相遇点开始走，另一个指针同步从链表起点开始走，步长都为1，当它们相遇时的点，就是环的起点。

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode * fast = head;
    struct ListNode * slow = head;
    struct ListNode * meet = head;
    struct ListNode * start = head;


    while(fast&&fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(slow == fast)
        {
            meet  = slow;
            while(start != meet)
            {
                start = start->next;
                meet = meet->next;
            }
            return meet;
        }

    }

    return NULL;
}

---

复制带随机指针的链表

 链接：力扣

 这道题还是有些难度的，画图分析很重要，逻辑原理不算困难，但是为了实现深度拷贝，我们还需要创建一个新链表。

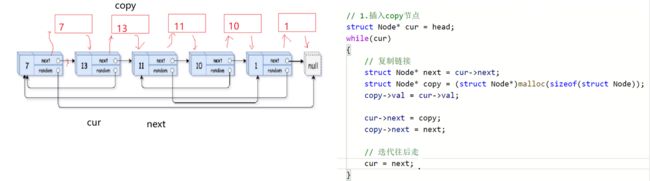
1.先拷贝原节点

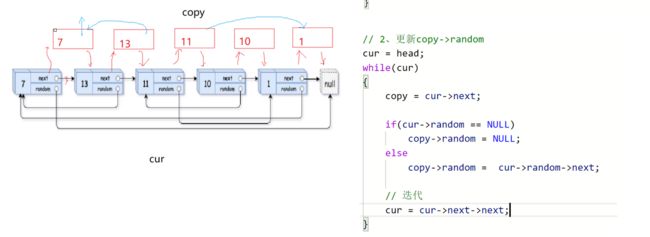
 2.更新每个拷贝节点的random值

 

 3.将创建好的拷贝节点整成一个新链表

 

---

至此，双向链表的OJ题细述结束

感谢阅读！希望对你有点帮助！