TimesNet 代码阅读

主函数 ./run.py

args = parser.parse_args()
args.use_gpu = True if torch.cuda.is_available() and args.use_gpu else False

if args.use_gpu and args.use_multi_gpu:
    args.dvices = args.devices.replace(' ', '')
    device_ids = args.devices.split(',')
    args.device_ids = [int(id_) for id_ in device_ids]
    args.gpu = args.device_ids[0]

print('Args in experiment:')
print(args)

if args.task_name == 'long_term_forecast':
    Exp = Exp_Long_Term_Forecast
elif args.task_name == 'short_term_forecast':
    Exp = Exp_Short_Term_Forecast
elif args.task_name == 'imputation':
    Exp = Exp_Imputation
elif args.task_name == 'anomaly_detection':
    Exp = Exp_Anomaly_Detection
elif args.task_name == 'classification':
    Exp = Exp_Classification
else:
    Exp = Exp_Long_Term_Forecast

if args.is_training:
    for ii in range(args.itr):
        # setting record of experiments
        setting = '{}_{}_{}_{}_ft{}_sl{}_ll{}_pl{}_dm{}_nh{}_el{}_dl{}_df{}_fc{}_eb{}_dt{}_{}_{}'.format(
            args.task_name,
            args.model_id,
            args.model,
            args.data,
            args.features,
            args.seq_len,
            args.label_len,
            args.pred_len,
            args.d_model,
            args.n_heads,
            args.e_layers,
            args.d_layers,
            args.d_ff,
            args.factor,
            args.embed,
            args.distil,
            args.des, ii)

        exp = Exp(args)  # set experiments
        print('>>>>>>>start training : {}>>>>>>>>>>>>>>>>>>>>>>>>>>'.format(setting))
        exp.train(setting)

        print('>>>>>>>testing : {}<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<'.format(setting))
        exp.test(setting)
        torch.cuda.empty_cache()

首先看exp = Exp(args) 这句。

数据读取 ./data_provider/data_loader.py

从

./run.py

调用Exp类，进入

./exp/exp_classification.py

；这里train_data, train_loader = self._get_data(flag='TRAIN') test_data, test_loader = self._get_data(flag='TEST')首先读取了一次训练集与测试集，目的是初始化网络结构。之后训练的时候还会再读取一次：

class Exp_Classification(Exp_Basic):
    def __init__(self, args):
        super(Exp_Classification, self).__init__(args)

    def _build_model(self):
        # model input depends on data
        train_data, train_loader = self._get_data(flag='TRAIN')
        test_data, test_loader = self._get_data(flag='TEST')
        self.args.seq_len = max(train_data.max_seq_len, test_data.max_seq_len)
        self.args.pred_len = 0
        self.args.enc_in = train_data.feature_df.shape[1]
        self.args.num_class = len(train_data.class_names)
        # model init
        model = self.model_dict[self.args.model].Model(self.args).float()
        if self.args.use_multi_gpu and self.args.use_gpu:
            model = nn.DataParallel(model, device_ids=self.args.device_ids)
        return model

    def _get_data(self, flag):
        data_set, data_loader = data_provider(self.args, flag)
        return data_set, data_loader

读取数据，先进入

./data_provider/data_factory.py

，可以发现调用的是UEAloader，位于

./data_provider/data_loader.py

class UEAloader(Dataset):
    """
    Dataset class for datasets included in:
        Time Series Classification Archive (www.timeseriesclassification.com)
    Argument:
        limit_size: float in (0, 1) for debug
    Attributes:
        all_df: (num_samples * seq_len, num_columns) dataframe indexed by integer indices, with multiple rows corresponding to the same index (sample).
            Each row is a time step; Each column contains either metadata (e.g. timestamp) or a feature.
        feature_df: (num_samples * seq_len, feat_dim) dataframe; contains the subset of columns of `all_df` which correspond to selected features
        feature_names: names of columns contained in `feature_df` (same as feature_df.columns)
        all_IDs: (num_samples,) series of IDs contained in `all_df`/`feature_df` (same as all_df.index.unique() )
        labels_df: (num_samples, num_labels) pd.DataFrame of label(s) for each sample
        max_seq_len: maximum sequence (time series) length. If None, script argument `max_seq_len` will be used.
            (Moreover, script argument overrides this attribute)
    """

    def __init__(self, root_path, file_list=None, limit_size=None, flag=None):
        self.root_path = root_path
        self.all_df, self.labels_df = self.load_all(root_path, file_list=file_list, flag=flag)
        self.all_IDs = self.all_df.index.unique()  # all sample IDs (integer indices 0 ... num_samples-1)

        if limit_size is not None:
            if limit_size > 1:
                limit_size = int(limit_size)
            else:  # interpret as proportion if in (0, 1]
                limit_size = int(limit_size * len(self.all_IDs))
            self.all_IDs = self.all_IDs[:limit_size]
            self.all_df = self.all_df.loc[self.all_IDs]

        # use all features
        self.feature_names = self.all_df.columns
        self.feature_df = self.all_df

        # pre_process
        normalizer = Normalizer()
        self.feature_df = normalizer.normalize(self.feature_df)
        # print(len(self.all_IDs))

    def load_all(self, root_path, file_list=None, flag=None):
        """
        Loads datasets from csv files contained in `root_path` into a dataframe, optionally choosing from `pattern`
        Args:
            root_path: directory containing all individual .csv files
            file_list: optionally, provide a list of file paths within `root_path` to consider.
                Otherwise, entire `root_path` contents will be used.
        Returns:
            all_df: a single (possibly concatenated) dataframe with all data corresponding to specified files
            labels_df: dataframe containing label(s) for each sample
        """
        # Select paths for training and evaluation
        if file_list is None:
            data_paths = glob.glob(os.path.join(root_path, '*'))  # list of all paths
        else:
            data_paths = [os.path.join(root_path, p) for p in file_list]
        if len(data_paths) == 0:
            raise Exception('No files found using: {}'.format(os.path.join(root_path, '*')))
        if flag is not None:
            data_paths = list(filter(lambda x: re.search(flag, x), data_paths))
        input_paths = [p for p in data_paths if os.path.isfile(p) and p.endswith('.ts')]
        if len(input_paths) == 0:
            raise Exception("No .ts files found using pattern: '{}'".format(pattern))

        all_df, labels_df = self.load_single(input_paths[0])  # a single file contains dataset

        return all_df, labels_df

    def load_single(self, filepath):
        df, labels = load_data.load_from_tsfile_to_dataframe(filepath, return_separate_X_and_y=True,
                                                             replace_missing_vals_with='NaN')
        labels = pd.Series(labels, dtype="category")
        self.class_names = labels.cat.categories
        labels_df = pd.DataFrame(labels.cat.codes,
                                 dtype=np.int8)  # int8-32 gives an error when using nn.CrossEntropyLoss

        lengths = df.applymap(
            lambda x: len(x)).values  # (num_samples, num_dimensions) array containing the length of each series

        horiz_diffs = np.abs(lengths - np.expand_dims(lengths[:, 0], -1))
        if np.sum(horiz_diffs) > 0:  # if any row (sample) has varying length across dimensions
            df = df.applymap(subsample)

        lengths = df.applymap(lambda x: len(x)).values
        vert_diffs = np.abs(lengths - np.expand_dims(lengths[0, :], 0))
        if np.sum(vert_diffs) > 0:  # if any column (dimension) has varying length across samples
            self.max_seq_len = int(np.max(lengths[:, 0]))
        else:
            self.max_seq_len = lengths[0, 0]


        df = pd.concat((pd.DataFrame({col: df.loc[row, col] for col in df.columns}).reset_index(drop=True).set_index(
            pd.Series(lengths[row, 0] * [row])) for row in range(df.shape[0])), axis=0)

        # Replace NaN values
        grp = df.groupby(by=df.index)
        df = grp.transform(interpolate_missing)

        return df, labels_df

网络训练与推理./exp/exp_classification

class Exp_Classification(Exp_Basic):
    def __init__(self, args):
        super(Exp_Classification, self).__init__(args)

    def _build_model(self):
        # model input depends on data
        train_data, train_loader = self._get_data(flag='TRAIN')
        test_data, test_loader = self._get_data(flag='TEST')
        self.args.seq_len = max(train_data.max_seq_len, test_data.max_seq_len)
        self.args.pred_len = 0
        self.args.enc_in = train_data.feature_df.shape[1]
        self.args.num_class = len(train_data.class_names)
        # model init
        model = self.model_dict[self.args.model].Model(self.args).float()
        if self.args.use_multi_gpu and self.args.use_gpu:
            model = nn.DataParallel(model, device_ids=self.args.device_ids)
        return model

    def _get_data(self, flag):
        data_set, data_loader = data_provider(self.args, flag)
        return data_set, data_loader

读取数据后，根据数据设置网络结构参数，之后初始化模型self.model_dict[self.args.model].Model(self.args).float()
其中`model_dict在

./exp/exp_classification.py定义

定义：

from models import Autoformer, Transformer, TimesNet, Nonstationary_Transformer, DLinear, FEDformer, \
    Informer, LightTS, Reformer, ETSformer, Pyraformer, PatchTST, MICN, Crossformer
class Exp_Basic(object):
    def __init__(self, args):
        self.args = args
        self.model_dict = {
            'TimesNet': TimesNet,
            'Autoformer': Autoformer,
            'Transformer': Transformer,
            'Nonstationary_Transformer': Nonstationary_Transformer,
            'DLinear': DLinear,
            'FEDformer': FEDformer,
            'Informer': Informer,
            'LightTS': LightTS,
            'Reformer': Reformer,
            'ETSformer': ETSformer,
            'PatchTST': PatchTST,
            'Pyraformer': Pyraformer,
            'MICN': MICN,
            'Crossformer': Crossformer,
        }
        self.device = self._acquire_device()
        self.model = self._build_model().to(self.device)

    def _build_model(self):
        raise NotImplementedError
        return None

所以就来到了

./models/TimesNet.py

的model函数：

class Model(nn.Module):
    """
    Paper link: https://openreview.net/pdf?id=ju_Uqw384Oq
    """

    def __init__(self, configs):
        super(Model, self).__init__()
        self.configs = configs
        self.task_name = configs.task_name
        self.seq_len = configs.seq_len
        self.label_len = configs.label_len
        self.pred_len = configs.pred_len
        self.model = nn.ModuleList([TimesBlock(configs)
                                    for _ in range(configs.e_layers)])
        self.enc_embedding = DataEmbedding(configs.enc_in, configs.d_model, configs.embed, configs.freq,
                                           configs.dropout)
        self.layer = configs.e_layers
        self.layer_norm = nn.LayerNorm(configs.d_model)
        if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
            self.predict_linear = nn.Linear(
                self.seq_len, self.pred_len + self.seq_len)
            self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)
        if self.task_name == 'imputation' or self.task_name == 'anomaly_detection':
            self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)
        if self.task_name == 'classification':
            self.act = F.gelu
            self.dropout = nn.Dropout(configs.dropout)
            self.projection = nn.Linear(
                configs.d_model * configs.seq_len, configs.num_class)

关注这一句：

        self.model = nn.ModuleList([TimesBlock(configs)
                                    for _ in range(configs.e_layers)])

可以发现网络是由许多个TimesBlock构成：

class TimesBlock(nn.Module):
    def __init__(self, configs):
        super(TimesBlock, self).__init__()
        self.seq_len = configs.seq_len
        self.pred_len = configs.pred_len
        self.k = configs.top_k
        # parameter-efficient design
        self.conv = nn.Sequential(
            Inception_Block_V1(configs.d_model, configs.d_ff,
                               num_kernels=configs.num_kernels),
            nn.GELU(),
            Inception_Block_V1(configs.d_ff, configs.d_model,
                               num_kernels=configs.num_kernels)
        )

    def forward(self, x):
        print(x.shape)
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)
        print('period_list',period_list.shape)
        print('period_weight',period_weight.shape)

        res = []
        for i in range(self.k):
            period = period_list[i]
            # padding
            if (self.seq_len + self.pred_len) % period != 0:
                length = (((self.seq_len + self.pred_len) // period) + 1) * period
                padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
                out = torch.cat([x, padding], dim=1)
            else:
                length = (self.seq_len + self.pred_len)
                out = x
            # reshape
            print('out-reshape-before',out.shape)
            out = out.reshape(B, length // period, period,
                              N).permute(0, 3, 1, 2).contiguous()
            print('out-reshape-after',out.shape)
            # 2D conv: from 1d Variation to 2d Variation
            out = self.conv(out)
            # reshape back
            out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
            print('out',out.shape)
            res.append(out[:, :(self.seq_len + self.pred_len), :])
            print('res',res.shape)
        res = torch.stack(res, dim=-1)
        print(res.shape)
        # adaptive aggregation
        period_weight = F.softmax(period_weight, dim=1)
        period_weight = period_weight.unsqueeze(
            1).unsqueeze(1).repeat(1, T, N, 1)
        res = torch.sum(res * period_weight, -1)
        # residual connection
        res = res + x
        return res

网络模型结构设计

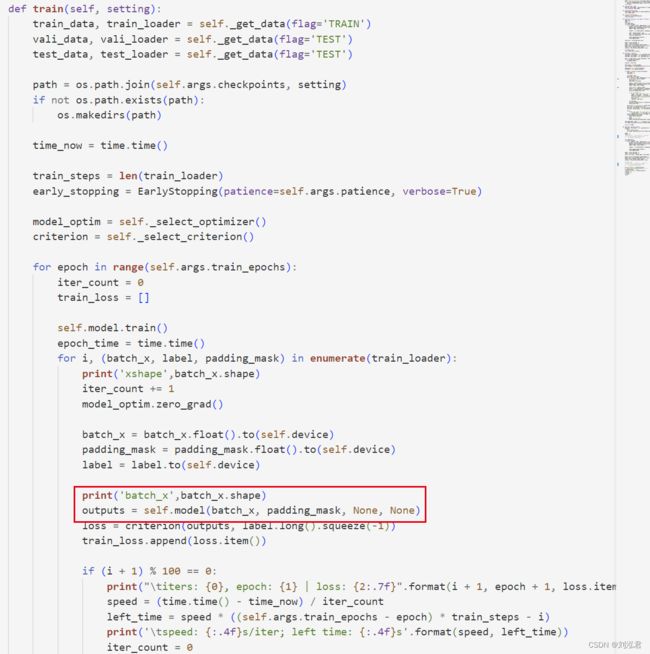
在batch_size输入时，x的shape是batch_x torch.Size([16, 29, 12])；

./exp/exp_classification.py

输入到self.model之后，
self.model = self._build_model().to(self.device)
model = self.model_dict[self.args.model].Model(self.args).float()

./model/TimesNet.py

class Model(nn.Module):
    """
    Paper link: https://openreview.net/pdf?id=ju_Uqw384Oq
    """

    def __init__(self, configs):
        super(Model, self).__init__()
        self.configs = configs
        self.task_name = configs.task_name
        self.seq_len = configs.seq_len
        self.label_len = configs.label_len
        self.pred_len = configs.pred_len
        self.model = nn.ModuleList([TimesBlock(configs)
                                    for _ in range(configs.e_layers)])
        self.enc_embedding = DataEmbedding(configs.enc_in, configs.d_model, configs.embed, configs.freq,
                                           configs.dropout)
        self.layer = configs.e_layers
        self.layer_norm = nn.LayerNorm(configs.d_model)
        if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
            self.predict_linear = nn.Linear(
                self.seq_len, self.pred_len + self.seq_len)
            self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)
        if self.task_name == 'imputation' or self.task_name == 'anomaly_detection':
            self.projection = nn.Linear(
                configs.d_model, configs.c_out, bias=True)
        if self.task_name == 'classification':
            self.act = F.gelu
            self.dropout = nn.Dropout(configs.dropout)
            self.projection = nn.Linear(
                configs.d_model * configs.seq_len, configs.num_class)

对于outputs = self.model(batch_x, padding_mask, None, None)，应该是直接调用forward()函数：

    def forward(self, x_enc, x_mark_enc, x_dec, x_mark_dec, mask=None):
        if self.task_name == 'long_term_forecast' or self.task_name == 'short_term_forecast':
            dec_out = self.forecast(x_enc, x_mark_enc, x_dec, x_mark_dec)
            return dec_out[:, -self.pred_len:, :]  # [B, L, D]
        if self.task_name == 'imputation':
            dec_out = self.imputation(
                x_enc, x_mark_enc, x_dec, x_mark_dec, mask)
            return dec_out  # [B, L, D]
        if self.task_name == 'anomaly_detection':
            dec_out = self.anomaly_detection(x_enc)
            return dec_out  # [B, L, D]
        if self.task_name == 'classification':
            dec_out = self.classification(x_enc, x_mark_enc)
            return dec_out  # [B, N]
        return None

在forward函数中print一下x_enc，还是x_enc forward: torch.Size([16, 29, 12])；

    def classification(self, x_enc, x_mark_enc):
        # embedding
        enc_out = self.enc_embedding(x_enc, None)  # [B,T,C]
        # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))

        # Output
        # the output transformer encoder/decoder embeddings don't include non-linearity
        output = self.act(enc_out)
        output = self.dropout(output)
        # zero-out padding embeddings
        output = output * x_mark_enc.unsqueeze(-1)
        # (batch_size, seq_length * d_model)
        output = output.reshape(output.shape[0], -1)
        output = self.projection(output)  # (batch_size, num_classes)
        return output
class DataEmbedding(nn.Module):
    def __init__(self, c_in, d_model, embed_type='fixed', freq='h', dropout=0.1):
        super(DataEmbedding, self).__init__()

        self.value_embedding = TokenEmbedding(c_in=c_in, d_model=d_model)
        self.position_embedding = PositionalEmbedding(d_model=d_model)
        self.temporal_embedding = TemporalEmbedding(d_model=d_model, embed_type=embed_type,
                                                    freq=freq) if embed_type != 'timeF' else TimeFeatureEmbedding(
            d_model=d_model, embed_type=embed_type, freq=freq)
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, x, x_mark):
        if x_mark is None:
            x = self.value_embedding(x) + self.position_embedding(x)
        else:
            x = self.value_embedding(
                x) + self.temporal_embedding(x_mark) + self.position_embedding(x)
        return self.dropout(x)

在embedding后，就变成了enc_out_classification torch.Size([16, 29, 64]).
其中，16是batch_size，29是length，12是通道数（维度数）；也就是说，他从12通道，变成了64通道。

FFT，频率变换：

for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))

调用了self.model:

    def forward(self, x):
        print(x.shape)
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)
        print('period_list',period_list.shape)
        print('period_weight',period_weight.shape)

        res = []
        for i in range(self.k):
            period = period_list[i]
            # padding
            if (self.seq_len + self.pred_len) % period != 0:
                length = (((self.seq_len + self.pred_len) // period) + 1) * period
                padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
                out = torch.cat([x, padding], dim=1)
            else:
                length = (self.seq_len + self.pred_len)
                out = x
            # reshape
            print('out-reshape-before',out.shape)
            out = out.reshape(B, length // period, period,
                              N).permute(0, 3, 1, 2).contiguous()
            print('out-reshape-after',out.shape)
            # 2D conv: from 1d Variation to 2d Variation
            out = self.conv(out)
            # reshape back
            out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
            print('out',out.shape)
            res.append(out[:, :(self.seq_len + self.pred_len), :])
            print('res',res.shape)
        res = torch.stack(res, dim=-1)
        print(res.shape)
        # adaptive aggregation
        period_weight = F.softmax(period_weight, dim=1)
        period_weight = period_weight.unsqueeze(
            1).unsqueeze(1).repeat(1, T, N, 1)
        res = torch.sum(res * period_weight, -1)
        # residual connection
        res = res + x
        return res

其中，FFT_for_Period函数是：

def FFT_for_Period(x, k=2):
    # [B, T, C]
    xf = torch.fft.rfft(x, dim=1)
    # find period by amplitudes
    frequency_list = abs(xf).mean(0).mean(-1)
    frequency_list[0] = 0
    _, top_list = torch.topk(frequency_list, k)
    top_list = top_list.detach().cpu().numpy()
    period = x.shape[1] // top_list
    return period, abs(xf).mean(-1)[:, top_list]

本次实验，top_k=3

Namespace(activation='gelu', anomaly_ratio=0.25, batch_size=16, c_out=7, checkpoints='./checkpoints/', d_ff=64, d_layers=1, d_model=64, data='UEA', data_path='ETTh1.csv', dec_in=7, des='Exp', devices='0,1,2,3', distil=True, dropout=0.1, e_layers=2, embed='timeF', enc_in=7, factor=1, features='M', freq='h', gpu=0, is_training=1, itr=1, label_len=48, learning_rate=0.001, loss='MSE', lradj='type1', mask_rate=0.25, model='TimesNet', model_id='JapaneseVowels', moving_avg=25, n_heads=8, num_kernels=6, num_workers=10, output_attention=False, p_hidden_dims=[128, 128], p_hidden_layers=2, patience=10, pred_len=96, root_path='./dataset/JapaneseVowels/', seasonal_patterns='Monthly', seq_len=96, target='OT', task_name='classification', top_k=3, train_epochs=30, use_amp=False, use_gpu=True, use_multi_gpu=False

计算FFT：

def FFT_for_Period(x, k=2):
    # [B, T, C]
    print('x',x.shape)
    xf = torch.fft.rfft(x, dim=1)
    # find period by amplitudes
    frequency_list = abs(xf).mean(0).mean(-1)
    frequency_list[0] = 0
    _, top_list = torch.topk(frequency_list, k)
    top_list = top_list.detach().cpu().numpy()
    print('x',x.shape)
    period = x.shape[1] // top_list
    print('xshape',x.shape[1])
    print('period',period)
    print('pe',period.shape)
    return period, abs(xf).mean(-1)[:, top_list]

对FFT代码的解释：

使用FFT算法来计算给定序列的频域表示。对于一个长度为N的输入序列，其FFT变换后的结果包含N/2+1个复数值，这些复数值表示了输入序列中不同频率成分的幅度和相位信息。在该函数中，通过计算每个频率分量的平均幅度来估计其重要性，并选取最高的k个频率分量作为周期的估计值。
在代码中，输入序列x的长度为29。函数计算了x的FFT变换结果xf，然后计算了每个频率分量的平均幅度。由于输入序列的长度为29，因此其FFT变换结果中有15个复数值（即N/2+1），对应于频率分量从0到14，其中0表示直流成分。在计算频率分量的平均幅度时，函数忽略了直流分量（即第一个复数值），因此得到了一个长度为14的频率分量幅度向量frequency_list。
abs(xf).mean(0).mean(-1) 的目的是计算频率成分的平均幅度，以便找到序列中最重要的频率。具体来说， abs(xf) 计算复数傅里叶变换的幅度，然后在 dim=0 上取平均值，得到每个频率成分的平均幅度。接下来，在 dim=-1 上取平均值，得到每个时间步的平均幅度。最终的结果是一个形状为 [T // 2 + 1] 的张量，其中每个元素代表相应频率成分的平均幅度。
top_list 是一个整数数组，其形状为 [k]，表示在 frequency_list 中具有最高值的 k 个频率成分的索引。这些索引可以通过 torch.topk 函数获得。top_list 中的每个元素都是一个整数，代表相应频率成分在 frequency_list 中的索引。
period 是一个整数张量，形状为 [B, k]，其中每个元素代表对应于 top_list 中的频率成分的周期。这个周期计算为输入序列长度除以相应的频率成分索引值。例如，如果 top_list[0] 的值为 2，则 period[0, 0] 将是输入序列的周期，即 T // 2。注意，这里的整数除法使用了 // 运算符。

在傅里叶变换中，一个时域信号可以表示为不同频率的正弦和余弦函数的叠加。在实数快速傅里叶变换中，一个时域信号的傅里叶变换结果包含了相应的频率成分和每个频率成分对应的幅度。对于实数信号而言，它的傅里叶变换是对称的，因此只需要考虑变换结果的前半部分（通常是 $T//2+1$ 个频率成分）。
在 abs(xf).mean(-1)[:, top_list] 表达式中，对傅里叶变换结果的操作会选择每个时间步的一组频率成分的幅度。这些频率成分通常是输入信号中出现频率较高的成分，可以用于描述输入信号中的周期性。例如，如果输入信号中有一个频率为 $f$ 的周期性模式，那么在傅里叶变换结果中，将会出现一个频率为 $f$ 的峰值，并且在 abs(xf).mean(-1)[:, top_list] 表达式中，会选择该峰值所对应的幅度作为该时间步的频率成分之一。对于所有时间步，不同的频率成分可能不同，这取决于输入信号的特点。
具体来说，在实数快速傅里叶变换中，输入信号的傅里叶变换结果包含了 $T//2+1$ 个频率成分，分别对应着 $0$ Hz、$1/T$ Hz、$2/T$ Hz、$\dots$、$(T//2)/T$ Hz 的频率。这些频率成分的幅度代表了输入信号在相应频率下的能量或权重。在 abs(xf).mean(-1)[:, top_list] 表达式中，为了寻找输入信号的周期性，我们选择了每个时间步中最具代表性的 $k$ 个频率成分，这些频率成分的幅度可以用于表示输入信号的周期性特征。因此，对于每个时间步，我们可以根据其频率成分的幅度来分析其周期性特征。

输出period，发现是29、14、9，也就是三个时序的周期（对应整个时序、一半时序和三分之一时序）；输出abs(xf).mean(-1)[:, top_list]，发现是一个数组[batch_size, top_list]，也即是[16,3]。

每个元素都代表了频率成分的幅度，所以此结果中就代表了周长为（29、14、9），也就是频率为（1Hz，2Hz，3Hz）信号的幅值。

时间步

如果时间步之间不同的话，为什么他的输出的形状只是[B,k]，而没有体现不同的时间步？不是[B,29,k]?
虽然在傅里叶变换中，每个时间步的频率成分是不同的，但是在 abs(xf).mean(-1)[:, top_list] 表达式中，我们选择了每个时间步的 $k$ 个最具代表性的频率成分的幅度作为输出，而没有保留所有时间步的幅度。因此，输出张量的形状只反映了在所有时间步中选择的 $k$ 个最具代表性的频率成分的幅度。如果要保留所有时间步的幅度，输出张量的形状应该是 [B, T, k]，其中 T 是输入序列的长度，但这样会导致输出张量的尺寸变得非常大，不便于后续的处理和分析。在某些情况下，我们可能只关注输入序列的全局周期性特征，而不是每个时间步的具体频率成分，因此输出形状为 [B, k] 的张量可能已经足够了。
这些频率成分是由整个序列的频率成分分布决定的，与时间步之间的具体数值无关。

总结FFT

总结一下，两个输出，一个period_list指不同的周长（29、14、9）的频率信号，一个period_weight指的是三个不同周长信号的频率幅值。

TimesBlock：

def forward(self, x):
        print(x.shape)
        B, T, N = x.size()
        period_list, period_weight = FFT_for_Period(x, self.k)
        print('period_list',period_list.shape)
        print('period_weight',period_weight.shape)

        res = []
        for i in range(self.k):
            period = period_list[i]
            # padding
            if (self.seq_len + self.pred_len) % period != 0:
                length = (((self.seq_len + self.pred_len) // period) + 1) * period
                padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
                out = torch.cat([x, padding], dim=1)
            else:
                length = (self.seq_len + self.pred_len)
                out = x
            # reshape
            print('out-reshape-before',out.shape)
            out = out.reshape(B, length // period, period,
                              N).permute(0, 3, 1, 2).contiguous()
            print('out-reshape-after',out.shape)
            # 2D conv: from 1d Variation to 2d Variation
            out = self.conv(out)
            # reshape back
            out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
            print('out',out.shape)
            res.append(out[:, :(self.seq_len + self.pred_len), :])
            print('res',res.shape)
        res = torch.stack(res, dim=-1)
        print(res.shape)
        # adaptive aggregation
        period_weight = F.softmax(period_weight, dim=1)
        period_weight = period_weight.unsqueeze(
            1).unsqueeze(1).repeat(1, T, N, 1)
        res = torch.sum(res * period_weight, -1)
        # residual connection
        res = res + x
        return res

首先，分别对三个period进行padding：

for i in range(self.k):
            period = period_list[i]
            # padding
            if (self.seq_len + self.pred_len) % period != 0:
                length = (((self.seq_len + self.pred_len) // period) + 1) * period
                padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)
                out = torch.cat([x, padding], dim=1)
            else:
                length = (self.seq_len + self.pred_len)
                out = x
            # reshape
            print('out-reshape-before',out.shape)
            out = out.reshape(B, length // period, period,
                              N).permute(0, 3, 1, 2).contiguous()
            print('out-reshape-after',out.shape)
            # 2D conv: from 1d Variation to 2d Variation
            out = self.conv(out)
            # reshape back
            out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
            print('out',out.shape)
            res.append(out[:, :(self.seq_len + self.pred_len), :])

padding后紧跟着reshape

padding没有什么好说的，可以看到第二个period和第三个period分别变成了42和36，就是分别能整除29、14和9。

reshape

reshape里来了重头戏，可以看到reshape后变成了二维（四维， [B, length//period, period, N] ），类比图像：每个二维张量对应于一幅二维图像，其中 N 是图像的通道数，length//period 是图像的高度，period 是图像的宽度

具体来说，该行代码的第一步是将 out 张量进行重塑，将其变形为 [B, length//period, period, N] 的形状，其中 B 是输入序列的批次大小，length 是输入序列经过填充后的长度，period 是当前周期特征的周期长度，N 是输入序列的通道数。这个重塑操作将输入序列划分为一系列周期性的子序列，每个子序列包含了 period 个时间步的数据。
接下来，该行代码通过 permute 方法对张量进行维度变换，将其变形为 [B, N, length//period, period] 的形状。这个变换操作的目的是将输入序列的时间维度和周期维度转置，并将它们放在张量的第三和第四个维度上，以方便后续卷积神经网络的处理。
最后，由于 permute 方法可能导致张量的存储方式不连续，该行代码使用 contiguous 方法来确保张量的存储方式连续。

此时，代码一维输入转化为二维输入：[B, N, length//period, period]，每个二维张量对应于一幅二维图像，其中 N 是图像的通道数，length//period 是图像的高度，period 是图像的宽度。本次实验，输入形状是【16，64，4，9】。

out = self.conv(out)
# reshape back
out = out.permute(0, 2, 3, 1).reshape(B, -1, N)
print('out',out.shape)
res.append(out[:, :(self.seq_len + self.pred_len), :])
res = torch.stack(res, dim=-1)

self.conv = nn.Sequential(
    Inception_Block_V1(configs.d_model, configs.d_ff,num_kernels=configs.num_kernels),
    nn.GELU(),
    Inception_Block_V1(configs.d_ff, configs.d_model,num_kernels=configs.num_kernels)
        )

class Inception_Block_V1(nn.Module):
    def __init__(self, in_channels, out_channels, num_kernels=6, init_weight=True):
        super(Inception_Block_V1, self).__init__()
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.num_kernels = num_kernels
        kernels = []
        for i in range(self.num_kernels):
            kernels.append(nn.Conv2d(in_channels, out_channels, kernel_size=2 * i + 1, padding=i))
        self.kernels = nn.ModuleList(kernels)
        if init_weight:
            self._initialize_weights()

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)

    def forward(self, x):
        res_list = []
        for i in range(self.num_kernels):
            res_list.append(self.kernels[i](x))
        res = torch.stack(res_list, dim=-1).mean(-1)
        return res

经过卷积神经网络的处理后，输出数据的形状为 [B, N, L//p, k]，其中 B 是输入序列的批次大小，N 是输入序列的特征数，L 是输入序列的长度（包括填充后的部分），p 是当前周期特征的周期长度，k 是卷积神经网络的卷积核个数。

之后，通过 permute 方法将张量的维度进行变换，将时间步和周期维度转置回原来的位置。

经过 permute 方法的变换，张量的维度被重新排列为 [B, L//p, k, N] 的形状，其中 B 是输入序列的批次大小，L 是输入序列的长度（包括填充后的部分），p 是当前周期特征的周期长度，k 是卷积神经网络的卷积核个数，N 是输入序列的特征数。

在这个形状中，第一维表示输入序列的批次大小，第二维表示输入序列经过周期划分后的子序列数量，第三维表示卷积神经网络生成的特征图数量，第四维表示每个特征图的通道数（即输入序列的特征数）。

然后，使用 reshape 方法将张量重塑为 [B, -1, N] 的形状，其中 -1 代表将其余维度压缩为一个维度，以便于后续处理。

res.append(out[:, :(self.seq_len + self.pred_len), :])这个选择操作的目的是去除填充后的部分，只保留输入序列和预测输出的部分。

分析结果，可以看到，最后三个通道都被截成了[16,29,64]；stack之后，变成了[16,29,64,3]。其中，29是时序数据长度，64是经过DataEmbedding之后的嵌入维度（包括嵌入层：值嵌入（value_embedding）、位置嵌入（position_embedding）和时间嵌入（temporal_embedding））。

之后，

period_weight = F.softmax(period_weight, dim=1)
        period_weight = period_weight.unsqueeze(
            1).unsqueeze(1).repeat(1, T, N, 1)
        res = torch.sum(res * period_weight, -1)
        # residual connection
        res = res + x

该部分代码首先使用 softmax 函数将每个周期特征的权重进行归一化，使得它们的和为 1。然后，该部分代码通过一系列重塑和广播操作将周期特征的权重扩展到与输入序列相同的形状，以便于后续计算。具体来说，该部分代码首先使用 unsqueeze 方法将周期特征的权重扩展为 [B, 1, 1, k] 的形状，然后使用 repeat 方法将其复制为 [B, T, N, k] 的形状，其中 T 是输入序列的长度，N 是输入序列的特征数。这个扩展操作的目的是将周期特征的权重与输入序列的每个时间步和特征维度对齐，以便于后续计算。

接下来，该部分代码使用点乘运算将周期特征的预测输出 res 与周期特征的权重进行加权，以得到加权平均的预测输出。具体来说，该部分代码使用 torch.sum 方法将 res 与 period_weight 相乘后在最后一维上求和，得到一个形状为 [B, T, N] 的张量。在这个过程中，周期特征的权重会对周期特征的预测输出进行加权平均，提高预测结果的表征能力。

最后，该部分代码将加权平均的预测输出 res 与输入序列 x 进行残差连接（residual connection），得到最终的预测结果。这个残差连接的目的是保留输入序列中的原始信息，并将周期特征的预测输出加到原始信息上，以得到更准确的预测结果。

classification

    def classification(self, x_enc, x_mark_enc):
        # embedding
        enc_out = self.enc_embedding(x_enc, None)  # [B,T,C]
        print('enc_out_classification',enc_out.shape)
        # TimesNet
        for i in range(self.layer):
            enc_out = self.layer_norm(self.model[i](enc_out))
        # Output
        # the output transformer encoder/decoder embeddings don't include non-linearity
        output = self.act(enc_out)
        output = self.dropout(output)
        print('output_classification1',output.shape)
        # zero-out padding embeddings
        output = output * x_mark_enc.unsqueeze(-1)
        print('output_classification2',output.shape)
        # (batch_size, seq_length * d_model)
        output = output.reshape(output.shape[0], -1)
        print('output_classification3',output.shape)
        output = self.projection(output)  # (batch_size, num_classes)
        print('output_classification4',output.shape)
        return output

这段代码用于对输入序列进行分类任务，即将输入序列映射为一个类别标签。

具体来说，该部分代码首先将输入序列 x_enc 和时间信息 x_mark_enc 分别输入到数据嵌入层 enc_embedding 中，得到一个形状为 [B, T, C] 的张量 enc_out，其中 B 是输入序列的批次大小，T 是输入序列的长度，C 是输入序列的特征数。然后，该部分代码将 enc_out 输入到一系列经过标准化的 TimesNet 模型中，以进行特征提取和表示学习。其中，该部分代码使用一个 for 循环来依次遍历 TimesNet 模型中的每个子模块，并使用标准化层对每个子模块的输出进行标准化。通过这些处理，该部分代码可以得到一个经过多层非线性变换的特征表示 enc_out。

接下来，该部分代码使用一个全连接层 projection 将 enc_out 映射为输出类别标签。具体来说，该部分代码首先使用激活函数（activation function）对 enc_out 进行非线性变换，以增强其表征能力。然后，该部分代码使用 dropout 层对变换后的特征进行正则化，并使用 reshape 方法将其变换为一个形状为 [B, T * C] 的张量。接着，该部分代码使用全连接层 projection 将变换后的特征映射为一个类别标签，得到一个形状为 [B, num_classes] 的张量 output，其中 num_classes 是输出的类别数量。

最后，该部分代码将 output 作为最终的分类结果返回。