第六届团队程序设计天梯赛 全题目解析讲解

B站已经录好视频合集：--------------------传送门---------------------
题目是2021年4月天梯赛决赛原题：

题号	题目名称
L1-1	人与神
L1-2	两小时学完C语言
L1-3	强迫症
L1-4	降价提醒机器人
L1-5	大笨钟的心情
L1-6	吉老师的回归
L1-7	天梯赛的善良
L1-8	乘法口诀数列
L2-1	包装机
L2-2	病毒溯源
L2-3	清点代码库
L2-4	哲哲打游戏
L3-1	森森旅游
L3-2	还原文件
L3-3	可怜的简单题

AC代码：

L1-1 人与神

跨界大神 L. Peter Deutsch 有一句名言：“To iterate is human, to recurse divine.”（迭代的是人，递归的是神）。本题就请你直接在屏幕上输出这句话。

输入格式：
本题没有输入。

输出格式：
在一行中输出 To iterate is human, to recurse divine.。

输入样例：
无
输出样例：
To iterate is human, to recurse divine.

#include 
using namespace std;

int main()
{
	printf("To iterate is human, to recurse divine.");
	return 0;
}

L1-2 两小时学完C语言

知乎上有个宝宝问：“两个小时内如何学完 C 语言？”当然，问的是“学完”并不是“学会”。

假设一本 C 语言教科书有 N 个字，这个宝宝每分钟能看 K 个字，看了 M 分钟。还剩多少字没有看？

输入格式：
输入在一行中给出 3 个正整数，分别是 N（不超过 400 000），教科书的总字数；K（不超过 3 000），是宝宝每分钟能看的字数；M（不超过 120），是宝宝看书的分钟数。

题目保证宝宝看完的字数不超过 N。

输出格式：
在一行中输出宝宝还没有看的字数。

输入样例：
100000 1000 72
输出样例：
28000

#include 
using namespace std;

int main()
{
	int a, b, c;
	cin >> a >> b >> c;
	cout << a - b * c << endl;
	return 0;
}

L1-3 强迫症

小强在统计一个小区里居民的出生年月，但是发现大家填写的生日格式不统一，例如有的人写 199808，有的人只写 9808。有强迫症的小强请你写个程序，把所有人的出生年月都整理成 年年年年-月月 格式。对于那些只写了年份后两位的信息，我们默认小于 22 都是 20 开头的，其他都是 19 开头的。

输入格式：
输入在一行中给出一个出生年月，为一个 6 位或者 4 位数，题目保证是 1000 年 1 月到 2021 年 12 月之间的合法年月。

输出格式：
在一行中按标准格式 年年年年-月月 将输入的信息整理输出。

输入样例 1：
9808
输出样例 1：
1998-08
输入样例 2：
0510
输出样例 2：
2005-10
输入样例 3：
196711
输出样例 3：
1967-11

#include 
using namespace std;

int main()
{
	int n;
	scanf("%d", &n);
	if(n < 10000) {
		int x = n / 100;
		if(x < 22)	cout << 20;
		else	cout << 19;
		if(x < 10)	cout << 0;
		cout << x;
		
		x = n % 100;
		cout << '-';
		if(x < 10)	cout << 0;
		cout << x;
	}
	else {
		int x = n / 100;
		if(x < 10)	cout << 0;
		cout << x << "-";
		x = n % 100;
		if(x < 10)	cout << 0;
		cout << x;
	}
	return 0;
}

L1-4 降价提醒机器人

小 T 想买一个玩具很久了，但价格有些高，他打算等便宜些再买。但天天盯着购物网站很麻烦，请你帮小 T 写一个降价提醒机器人，当玩具的当前价格比他设定的价格便宜时发出提醒。

输入格式：
输入第一行是两个正整数 N 和 M (1≤N≤100,0≤M≤1000)，表示有 N 条价格记录，小 T 设置的价格为 M。

接下来 N 行，每行有一个实数 Pi​（−1000.0

输出格式：
对每一条比设定价格 M 便宜的价格记录 P，在一行中输出 On Sale! P，其中 P 输出到小数点后 1 位。

输入样例：
4 99
98.0
97.0
100.2
98.9
输出样例：
On Sale! 98.0
On Sale! 97.0
On Sale! 98.9

#include 
using namespace std;

int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) {
		double x;
		scanf("%lf", &x);
		if(x < m) 
			printf("On Sale! %.1lf\n", x);
	}
	return 0;
}

L1-5 大笨钟的心情

有网友问：未来还会有更多大笨钟题吗？笨钟回复说：看心情……

本题就请你替大笨钟写一个程序，根据心情自动输出回答。

输入格式：
输入在一行中给出 24 个 [0, 100] 区间内的整数，依次代表大笨钟在一天 24 小时中，每个小时的心情指数。

随后若干行，每行给出一个 [0, 23] 之间的整数，代表网友询问笨钟这个问题的时间点。当出现非法的时间点时，表示输入结束，这个非法输入不要处理。题目保证至少有 1 次询问。

输出格式：
对每一次提问，如果当时笨钟的心情指数大于 50，就在一行中输出 心情指数 Yes，否则输出 心情指数 No。

输入样例：
80 75 60 50 20 20 20 20 55 62 66 51 42 33 47 58 67 52 41 20 35 49 50 63
17
7
3
15
-1
输出样例：
52 Yes
20 No
50 No
58 Yes

#include 
using namespace std;
int a[24];
int main()
{
	for(int i = 0; i < 24; i++)	scanf("%d", &a[i]);
	while(1) {
		int x;
		scanf("%d", &x);
		if(x < 0 || x > 23)	break;
		if(a[x] > 50)	printf("%d Yes\n", a[x]);
		else	printf("%d No\n", a[x]);
	}
	return 0;
}

L1-6 吉老师的回归

曾经在天梯赛大杀四方的吉老师决定回归天梯赛赛场啦！

为了简化题目，我们不妨假设天梯赛的每道题目可以用一个不超过 500 的、只包括可打印符号的字符串描述出来，如：Problem A: Print “Hello world!”。

众所周知，吉老师的竞赛水平非常高超，你可以认为他每道题目都会做（事实上也是……）。因此，吉老师会按照顺序看题并做题。但吉老师水平太高了，所以签到题他就懒得做了（浪费时间），具体来说，假如题目的字符串里有 qiandao 或者 easy（区分大小写）的话，吉老师看完题目就会跳过这道题目不做。

现在给定这次天梯赛总共有几道题目以及吉老师已经做完了几道题目，请你告诉大家吉老师现在正在做哪个题，或者吉老师已经把所有他打算做的题目做完了。

提醒：天梯赛有分数升级的规则，如果不做签到题可能导致团队总分不足以升级，一般的选手请千万不要学习吉老师的酷炫行为！

输入格式：
输入第一行是两个正整数 N,M (1≤M≤N≤30)，表示本次天梯赛有 N 道题目，吉老师现在做完了 M 道。

接下来 N 行，每行是一个符合题目描述的字符串，表示天梯赛的题目内容。吉老师会按照给出的顺序看题——第一行就是吉老师看的第一道题，第二行就是第二道，以此类推。

输出格式：
在一行中输出吉老师当前正在做的题目对应的题面（即做完了 M 道题目后，吉老师正在做哪个题）。如果吉老师已经把所有他打算做的题目做完了，输出一行 Wo AK le。

输入样例 1：
5 1
L1-1 is a qiandao problem.
L1-2 is so…easy.
L1-3 is Easy.
L1-4 is qianDao.
Wow, such L1-5, so easy.
输出样例 1：
L1-4 is qianDao.
输入样例 2：
5 4
L1-1 is a-qiandao problem.
L1-2 is so easy.
L1-3 is Easy.
L1-4 is qianDao.
Wow, such L1-5, so!!easy.
输出样例 2：
Wo AK le

#include 
using namespace std;
int main()
{
	int n, m;
	string s;
	scanf("%d %d\n", &n, &m);
	for(int i = 1; i <= n; i++) {
		getline(cin, s);
		int len = s.size();
		bool flag = true; //flag为true的时候，说明这行字符串不包含easy或qiandao 
		for(int j = 0; j < len; j++) {
			if(j + 3 < len) {
				if(s[j] == 'e' && s[j+1] == 'a' && s[j+2] == 's' && s[j+3] == 'y')	// 说明包含easy
					flag = false;	// pass 
			}
			if(j + 6 < len) {
				if(s[j] == 'q' && s[j+1] == 'i' && s[j+2] == 'a' && s[j+3] == 'n' && s[j+4] == 'd' && s[j+5] == 'a' && s[j+6] =='o')
					flag = false; 	// pass 
			}
		}
		if(flag == true)	m--;
		if(m == -1) {
			cout << s << endl;
			return 0;
		}
	}
	cout << "Wo AK le" << endl;
	return 0;
}

L1-7 天梯赛的善良

天梯赛是个善良的比赛。善良的命题组希望将题目难度控制在一个范围内，使得每个参赛的学生都有能做出来的题目，并且最厉害的学生也要非常努力才有可能得到高分。

于是命题组首先将编程能力划分成了 10^6个等级（太疯狂了，这是假的），然后调查了每个参赛学生的编程能力。现在请你写个程序找出所有参赛学生的最小和最大能力值，给命题组作为出题的参考。

输入格式：
输入在第一行中给出一个正整数 N（≤2×10^4 ），即参赛学生的总数。随后一行给出 N 个不超过 10^6的正整数，是参赛学生的能力值。

输出格式：
第一行输出所有参赛学生的最小能力值，以及具有这个能力值的学生人数。第二行输出所有参赛学生的最大能力值，以及具有这个能力值的学生人数。同行数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：
10
86 75 233 888 666 75 886 888 75 666
输出样例：
75 3
888 2

#include 
using namespace std;
const int Maxn = 20000 + 20;
int n, f[Maxn];
int main()
{
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	scanf("%d", &f[i]);//[1,n]
	sort(f + 1, f + 1 + n); //[1, n+1)
	int cnt1 = 0, cnt2 = 0;
	for(int i = 1; i <= n; i++) {
		if(f[i] == f[1])	cnt1++;
		if(f[i] == f[n])	cnt2++;
	}
	printf("%d %d\n%d %d", f[1], cnt1, f[n], cnt2);
//	n * logn
	/*
	int Max = f[1], Min = f[1];
	for(int i = 2; i <= n; i++) {
		if(f[i] > Max)	Max = f[i];
		if(f[i] < Min)	Min = f[i];
	}
	int cnt1 = 0, cnt2 = 0;
	for(int i = 1; i <= n; i++) {
		if(f[i] == Min)	cnt1++;
		if(f[i] == Max)	cnt2++;
	}
	printf("%d %d\n%d %d", Min, cnt1, Max, cnt2); 
	*/
//	O(n)
	return 0;
}

L1-8 乘法口诀数列

本题要求你从任意给定的两个 1 位数字 a1​和a2开始，用乘法口诀生成一个数列 {an​}，规则为从a1​开始顺次进行，每次将当前数字与后面一个数字相乘，将结果贴在数列末尾。如果结果不是 1 位数，则其每一位都应成为数列的一项。

输入格式：
输入在一行中给出 3 个整数，依次为 a1​、a2​和n，满足 0≤a1​,a2​≤9，0

输出格式：
在一行中输出数列的前 n 项。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：
2 3 10
输出样例：
2 3 6 1 8 6 8 4 8 4
样例解释：
数列前 2 项为 2 和 3。从 2 开始，因为 2×3=6，所以第 3 项是 6。因为 3×6=18，所以第 4、5 项分别是 1、8。依次类推…… 最后因为第 6 项有 6×8=48，对应第 10、11 项应该是 4、8。而因为只要求输出前 10 项，所以在输出 4 后结束。

#include 
using namespace std;
const int Maxn = 1000 + 10;
int n, f[Maxn];
int main()
{
	scanf("%d%d%d", &f[1], &f[2], &n);
	int cnt = 3;
	for(int i = 1; i <= 1000; i++) {
		int x = f[i] * f[i + 1];
		if(x < 10) {
			f[cnt++] = x;
//			cnt++;
		}
		else {
			f[cnt++] = x / 10; // cnt++;
			f[cnt++] = x % 10; //cnt++;
		}
		if(cnt > n)	break;
	}
	for(int i = 1; i < n; i++)
		printf("%d ", f[i]);
	printf("%d", f[n]);
	return 0;
}

L2-1 包装机

一种自动包装机的结构如图 1 所示。首先机器中有 N 条轨道，放置了一些物品。轨道下面有一个筐。当某条轨道的按钮被按下时，活塞向左推动，将轨道尽头的一件物品推落筐中。当 0 号按钮被按下时，机械手将抓取筐顶部的一件物品，放到流水线上。图 2 显示了顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态。

图1 自动包装机的结构

图 2 顺序按下按钮 3、2、3、0、1、2、0 后包装机的状态

一种特殊情况是，因为筐的容量是有限的，当筐已经满了，但仍然有某条轨道的按钮被按下时，系统应强制启动 0 号键，先从筐里抓出一件物品，再将对应轨道的物品推落。此外，如果轨道已经空了，再按对应的按钮不会发生任何事；同样的，如果筐是空的，按 0 号按钮也不会发生任何事。

现给定一系列按钮操作，请你依次列出流水线上的物品。

输入格式：
输入第一行给出 3 个正整数 N（≤100）、M（≤1000）和 Smax（≤100），分别为轨道的条数（于是轨道从 1 到 N 编号）、每条轨道初始放置的物品数量、以及筐的最大容量。随后 N 行，每行给出 M 个英文大写字母，表示每条轨道的初始物品摆放。

最后一行给出一系列数字，顺序对应被按下的按钮编号，直到 −1 标志输入结束，这个数字不要处理。数字间以空格分隔。题目保证至少会取出一件物品放在流水线上。

输出格式：
在一行中顺序输出流水线上的物品，不得有任何空格。

输入样例：
3 4 4
GPLT
PATA
OMSA
3 2 3 0 1 2 0 2 2 0 -1
输出样例：
MATA

/* 
stack:
stack  sta;
	sta.push(2); //放 
	sta.top(); //读取顶层元素 
	sta.pop(); //弹出顶层元素（删除） 
	sta.size(); // 读取栈的大小 返回类型是int，  int siz = sta.size();
	sta.empty(); // 为空的时候返回true，不为空返回的是false 
queue:
queue  q;
	q.push(2); //放
	q.front(); //读取队列头元素
	q.pop(); // 弹出队列头的元素 
	q.size(); // 读取队列的大小 返回类型是int，  int siz = q.size();
	q.empty(); // 为空的时候返回true，不为空返回的是false 
*/
#include 
using namespace std;
const int Maxn = 100 + 10;
const int Maxm = 1000 + 10;
int n, m, Max;
char s[Maxn][Maxm];
int ptr[Maxn];
stack <char> sta;
int main()
{
	scanf("%d%d%d", &n, &m, &Max);
	for(int i = 1; i <= n; i++)	scanf("%s", s[i] + 1); // s[1][1]  s[1][2]  s[1][3]
	for(int i = 1; i <= n; i++)	ptr[i] = 1; //第 i 条轨道上该取第一个物品 
	while(1) {
		int x;
		scanf("%d", &x);
		
		if(x == -1)	break;
		else if(ptr[x] == m + 1)	continue;
		else if(x == 0 && sta.empty())	continue;
		
		if(sta.size() == Max) {
			printf("%c", sta.top());
			sta.pop();
			if(x != 0)
				sta.push(s[x][ptr[x]++]);
//				ptr[x]++;
		}
		else if(x == 0) {
			printf("%c", sta.top());
			sta.pop();
		}
		else	sta.push(s[x][ptr[x]++]);
	}
	return 0;
}

L2-2 病毒溯源

病毒容易发生变异。某种病毒可以通过突变产生若干变异的毒株，而这些变异的病毒又可能被诱发突变产生第二代变异，如此继续不断变化。

现给定一些病毒之间的变异关系，要求你找出其中最长的一条变异链。

在此假设给出的变异都是由突变引起的，不考虑复杂的基因重组变异问题 —— 即每一种病毒都是由唯一的一种病毒突变而来，并且不存在循环变异的情况。

输入格式：
输入在第一行中给出一个正整数 N（≤10^4 ），即病毒种类的总数。于是我们将所有病毒从 0 到 N−1 进行编号。

随后 N 行，每行按以下格式描述一种病毒的变异情况：

k 变异株1 …… 变异株k
其中 k 是该病毒产生的变异毒株的种类数，后面跟着每种变异株的编号。第 i 行对应编号为 i 的病毒（0≤i

输出格式：
首先输出从源头开始最长变异链的长度。

在第二行中输出从源头开始最长的一条变异链，编号间以 1 个空格分隔，行首尾不得有多余空格。如果最长链不唯一，则输出最小序列。

注：我们称序列 {a1 ,⋯,an } 比序列 { b1 ,⋯,bn} “小”，如果存在 1≤k≤n 满足 ai=bi对所有 i 输入样例：
10
3 6 4 8
0
0
0
2 5 9
0
1 7
1 2
0
2 3 1
输出样例：
4
0 4 9 1

// 图论建边：采用邻接链表（不是用数据结构课学的代码）
// dfs（深度优先算法找最长链）
// 序列比较（代码基本功）
#include 
using namespace std;
const int Maxn = 10000 + 10;
const int Maxm = 200000 + 20;
int Ans[Maxn], temp[Maxn];
int n, Maxdeep, ecnt, head[Maxn], rd[Maxn]; // head[i]表示点i的出边信息的最后一次信息，比如i-->j，i-->l... 
struct list {
	int to; //边指向的点，比如a--->b，记录的就是b
	int nxt; // 下一条边 
}e[Maxm];
void add_edge(int u, int v) {// 表示建立了一条从点u到点v的有向边
	e[++ecnt].to = v;
	e[ecnt].nxt = head[u];
	head[u] = ecnt;
}

bool check(int deep) {
	for(int i = 1; i <= deep; i++) 
		if(temp[i] > Ans[i])	return false;
		else if(temp[i] < Ans[i])	return true;
}

void dfs(int x, int deep) { //当前的点的编号是x，当前的链长是deep 
	temp[deep] = x;
	
	if(head[x] == 0) { //这个点走到头了，他不会突变成别的病毒了，这个点没有出边
		if(deep > Maxdeep) {
			for(int i = 1; i <= deep; i++)
				Ans[i] = temp[i];
			Maxdeep = deep;
		} 
		else if(deep == Maxdeep) {
			if(check(deep) == true)
				for(int i = 1; i <= deep; i++)
					Ans[i] = temp[i];
		}
		return;
	}
	
	for(int i = head[x]; i; i = e[i].nxt) { // 邻接链表的使用 
		int To = e[i].to;
		dfs(To, deep + 1);
	}
}
int main()
{
	scanf("%d", &n);
	for(int u = 0; u < n; u++) {
		int k;
		scanf("%d", &k);
		for(int j = 1; j <= k; j++) {
			int v;
			scanf("%d", &v);
			add_edge(u, v);
			rd[v]++;
		}
	}
	for(int i = 0; i < n; i++) {
		if(!rd[i]) {
			dfs(i, 1); // 从点i开始进行搜索，当前搜索的链长为1; 
		}
	}
	printf("%d\n", Maxdeep);
	for(int i = 1; i < Maxdeep; i++)
		printf("%d ", Ans[i]);
	printf("%d", Ans[Maxdeep]);
	return 0;
}

L2-3 清点代码库

上图转自新浪微博：“阿里代码库有几亿行代码，但其中有很多功能重复的代码，比如单单快排就被重写了几百遍。请设计一个程序，能够将代码库中所有功能重复的代码找出。各位大佬有啥想法，我当时就懵了，然后就挂了。。。”

这里我们把问题简化一下：首先假设两个功能模块如果接受同样的输入，总是给出同样的输出，则它们就是功能重复的；其次我们把每个模块的输出都简化为一个整数（在 int 范围内）。于是我们可以设计一系列输入，检查所有功能模块的对应输出，从而查出功能重复的代码。你的任务就是设计并实现这个简化问题的解决方案。

输入格式：
输入在第一行中给出 2 个正整数，依次为 N（≤10^4）和 M（≤10^2），对应功能模块的个数和系列测试输入的个数。

随后 N 行，每行给出一个功能模块的 M 个对应输出，数字间以空格分隔。

输出格式：
首先在第一行输出不同功能的个数 K。随后 K 行，每行给出具有这个功能的模块的个数，以及这个功能的对应输出。数字间以 1 个空格分隔，行首尾不得有多余空格。输出首先按模块个数非递增顺序，如果有并列，则按输出序列的递增序给出。

注：所谓数列 { A1 , …, AM } 比 { B1 , …, BM} 大，是指存在 1≤iBi+1。

输入样例：
7 3
35 28 74
-1 -1 22
28 74 35
-1 -1 22
11 66 0
35 28 74
35 28 74
输出样例：
4
3 35 28 74
2 -1 -1 22
1 11 66 0
1 28 74 35

// map:
/*
map  mp;
mp['c'] = 2;
printf("%d", mp['c']);

map  mp;
mp[1] = 2;
printf("%d", mp[1]);
*/ 
// vector:
// 自定义排序
#include 
using namespace std;
int n, m;
map <vector<int>, int> mp; 

struct pro {
	vector <int> v;
	int c;
	bool operator < (const pro& vv) const {
		if(c == vv.c)	return v < vv.v;
		return c > vv.c;
	}
};
vector <pro> ans;
int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 0; i < n; i++) {
		vector <int> v;
		for(int j = 0; j < m; j++) {
			int x;
			scanf("%d", &x);
			v.push_back(x);
		}
		if(mp.count(v))	mp[v]++;
		else	mp[v] = 1;
	}
	printf("%d\n", mp.size());
	for(auto i : mp) {
		pro t;
		t.c = i.second, t.c = i.first();
		ans.push_back(t);
	}
	sort(ans.begin(), ans.end());
	for(auto i : ans) {
		printf("%d", i.c);
		for(auto j : i.v)	printf(" %d", j);
		printf("\n");
	}
	return 0;
}

L2-4 哲哲打游戏

哲哲是一位硬核游戏玩家。最近一款名叫《达诺达诺》的新游戏刚刚上市，哲哲自然要快速攻略游戏，守护硬核游戏玩家的一切！

为简化模型，我们不妨假设游戏有 N 个剧情点，通过游戏里不同的操作或选择可以从某个剧情点去往另外一个剧情点。此外，游戏还设置了一些存档，在某个剧情点可以将玩家的游戏进度保存在一个档位上，读取存档后可以回到剧情点，重新进行操作或者选择，到达不同的剧情点。

为了追踪硬核游戏玩家哲哲的攻略进度，你打算写一个程序来完成这个工作。假设你已经知道了游戏的全部剧情点和流程，以及哲哲的游戏操作，请你输出哲哲的游戏进度。

输入格式：
输入第一行是两个正整数 N 和 M (1≤N,M≤10^5)，表示总共有 N 个剧情点，哲哲有 M 个游戏操作。
接下来的 N 行，每行对应一个剧情点的发展设定。第 i 行的第一个数字是 Ki​，表示剧情点 i 通过一些操作或选择能去往下面 Ki​个剧情点；接下来有 Ki​个数字，第 k 个数字表示做第 k 个操作或选择可以去往的剧情点编号。

最后有 M 行，每行第一个数字是 0、1 或 2，分别表示：

0 表示哲哲做出了某个操作或选择，后面紧接着一个数字 j，表示哲哲在当前剧情点做出了第 j 个选择。我们保证哲哲的选择永远是合法的。
1 表示哲哲进行了一次存档，后面紧接着是一个数字 j，表示存档放在了第 j 个档位上。
2 表示哲哲进行了一次读取存档的操作，后面紧接着是一个数字 j，表示读取了放在第 j 个位置的存档。
约定：所有操作或选择以及剧情点编号都从 1 号开始。存档的档位不超过 100 个，编号也从 1 开始。游戏默认从 1 号剧情点开始。总的选项数（即 ∑Ki​）不超过 10^6。

输出格式：
对于每个 1（即存档）操作，在一行中输出存档的剧情点编号。
最后一行输出哲哲最后到达的剧情点编号。

输入样例：
10 11
3 2 3 4
1 6
3 4 7 5
1 3
1 9
2 3 5
3 1 8 5
1 9
2 8 10
0
1 1
0 3
0 1
1 2
0 2
0 2
2 2
0 3
0 1
1 1
0 2
输出样例：
1
3
9
10
样例解释：
简单给出样例中经过的剧情点顺序：

1 -> 4 -> 3 -> 7 -> 8 -> 3 -> 5 -> 9 -> 10。

档位 1 开始存的是 1 号剧情点；档位 2 存的是 3 号剧情点；档位 1 后来又存了 9 号剧情点。

// s[i][j] = k  表示在 剧情点i的第j个选择是通向剧情k的 
// vector  s[100000 + 10];  
#include 
using namespace std;
const int Maxn = 100000 + 10;
int n, m, now = 1;
int rec[110];
vector <int> vec[Maxn];
int main() {
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++) {
		int k;
		scanf("%d", &k);
		for(int j = 1; j <= k; j++) {
			int v;
			scanf("%d", &v);
			vec[i].push_back(v); // vec[1][0] = 2, vec[1][1] = 3 ...
		}
	}
	for(int i = 1; i <= m; i++) {
		int a, b;
		scanf("%d%d", &a, &b);
		if(a == 0) {
			// now 现在的剧情点 
			// vec[now][b - 1] 将要到达的剧情点
			now = vec[now][b - 1]; 
		}
		else if(a == 1) {
			printf("%d\n", now);
			rec[b] = now;
		}
		else if(a == 2) {
			now = rec[b];
		}
	}
	printf("%d", now);
	return 0;
}

L3-1 森森旅游

好久没出去旅游啦！森森决定去 Z 省旅游一下。

Z 省有 n 座城市（从 1 到 n 编号）以及 m 条连接两座城市的有向旅行线路（例如自驾、长途汽车、火车、飞机、轮船等），每次经过一条旅行线路时都需要支付该线路的费用（但这个收费标准可能不止一种，例如车票跟机票一般不是一个价格）。

Z 省为了鼓励大家在省内多逛逛，推出了旅游金计划：在 i 号城市可以用 1 元现金兑换 ai​元旅游金（只要现金足够，可以无限次兑换）。城市间的交通即可以使用现金支付路费，也可以用旅游金支付。具体来说，当通过第 j 条旅行线路时，可以用 cj元现金或 dj元旅游金支付路费。注意： 每次只能选择一种支付方式，不可同时使用现金和旅游金混合支付。但对于不同的线路，旅客可以自由选择不同的支付方式。

森森决定从 1 号城市出发，到 n 号城市去。他打算在出发前准备一些现金，并在途中的某个城市将剩余现金 全部 换成旅游金后继续旅游，直到到达 n 号城市为止。当然，他也可以选择在 1 号城市就兑换旅游金，或全部使用现金完成旅程。

Z 省政府会根据每个城市参与活动的情况调整汇率（即调整在某个城市 1 元现金能换多少旅游金）。现在你需要帮助森森计算一下，在每次调整之后最少需要携带多少现金才能完成他的旅程。

输入格式:
输入在第一行给出三个整数 n，m 与 q（1≤n≤10^5， 1≤m≤2×10 ^5，1≤q≤10 ^5），依次表示城市的数量、旅行线路的数量以及汇率调整的次数。

接下来 m 行，每行给出四个整数 u，v，c 与 d（1≤u,v≤n，1≤c,d≤10^9），表示一条从 u 号城市通向 v 号城市的有向旅行线路。每次通过该线路需要支付 c 元现金或 d 元旅游金。数字间以空格分隔。输入保证从 1 号城市出发，一定可以通过若干条线路到达 n 号城市，但两城市间的旅行线路可能不止一条，对应不同的收费标准；也允许在城市内部游玩（即 u 和 v 相同）。

接下来的一行输入 n 个整数 a1,a2,⋯,an（1≤ai≤10^9），其中 ai表示一开始在 i 号城市能用 1 元现金兑换ai个旅游金。数字间以空格分隔。
接下来 q 行描述汇率的调整。第 i 行输入两个整数 xi与ai′（1≤xi≤n，1≤ai′≤10^9），表示第 i 次汇率调整后，xi号城市能用 1 元现金兑换 ai′​个旅游金，而其它城市旅游金汇率不变。请注意：每次汇率调整都是在上一次汇率调整的基础上进行的。

输出格式:
对每一次汇率调整，在对应的一行中输出调整后森森至少需要准备多少现金，才能按他的计划从 1 号城市旅行到 n 号城市。

再次提醒：如果森森决定在途中的某个城市兑换旅游金，那么他必须将剩余现金全部、一次性兑换，剩下的旅途将完全使用旅游金支付。

输入样例:
6 11 3
1 2 3 5
1 3 8 4
2 4 4 6
3 1 8 6
1 3 10 8
2 3 2 8
3 4 5 3
3 5 10 7
3 3 2 3
4 6 10 12
5 6 10 6
3 4 5 2 5 100
1 2
2 1
1 17
输出样例:
8
8
1
样例解释:
对于第一次汇率调整，森森可以沿着 1→2→4→6 的线路旅行，并在 2 号城市兑换旅游金；

对于第二次汇率调整，森森可以沿着 1→2→3→4→6 的线路旅行，并在 3 号城市兑换旅游金；

对于第三次汇率调整，森森可以沿着 1→3→5→6 的线路旅行，并在 1 号城市兑换旅游金。

// 迪杰斯特拉算法：  求一个点到其他所有点的距离(n^2)(优先队列优化，n*logn) 
// 本题题意要的解法： 至少要求出点1到其他所有点的距离（n*logn）。
//				再求出每个点到点n的距离..（建立反向边， 改成了求点n到其他点的距离） 
// 对于每个点ui就都能求出：到 点ui时的花费现金数量qi， 点ui到点n花费的旅游金数量pi ，至少要带qi+[pi/ai] ([]表示向上取整） 
// 邻接表建边、迪杰斯特拉算法、会使用优先队列、pair类型的使用 



// 高等数据结构：线段树 （修改操作是logn（单点修改，不是区间修改），查询操作也是logn，单独查询最小值的话是1） 
// 查询的复杂度就降低成了 q*logn


// 题目整体复杂度 max(n * logn, q * logn), n和q是等阶的 

#include 
using namespace std;
const int Maxn = 100000 + 10;
const int Maxm = 200000 + 20;
int n, m, t;
long long tree[Maxn << 2]; // 记录到达每个点的花费，同时也能记录一段区间的最小花费 
int a[Maxn];
int ecnt, head[Maxn];
int cecnt, chead[Maxn];
long long dis[Maxn], cdis[Maxn]; // dis[i]表示点1到点i的距离   cdisn[i] 表示点n到点i的距离（反向边）
bool vis[Maxn]; //表示点i是否作为最短路点进行了对其他点最短路的更新 
typedef pair<long long, int> pii;
priority_queue <pii, vector<pii>, greater<pii> > q; // 声明好了一个按最小值排序的小顶堆（也就是优先队列） 
struct list {
	int to, nxt, w;
}e[Maxm], ce[Maxm];
void add_edge(int u, int v, int w) {
	e[++ecnt].to = v;
	e[ecnt].w = w;
	e[ecnt].nxt = head[u];
	head[u] = ecnt;
}
void add_cedge(int u, int v, int w) {
	ce[++cecnt].to = v;
	ce[cecnt].w = w;
	ce[cecnt].nxt = chead[u];
	chead[u] = cecnt;
} 

void build_tree(int cur, int l, int r) {
	if(l == r) {
		if(dis[l] == 1e18 || cdis[l] == 1e18)	tree[cur] = 2e18;
		else	tree[cur] = dis[l] + (cdis[l] / a[l] + (cdis[l] % a[l] != 0)); 
		return;
	}
	int mid = l + r >> 1;
	build_tree(cur << 1, l, mid);
	build_tree(cur << 1 | 1, mid + 1, r);
	tree[cur] = min(tree[cur << 1], tree[cur << 1 | 1]);
}

void modify(int cur, int l, int r, int tar, int val) {
	if(l == r) {
		a[l] = val;
		if(dis[l] == 1e18 || cdis[l] == 1e18)	tree[cur] = 2e18;
		else	tree[cur] = dis[l] + (cdis[l] / a[l] + (cdis[l] % a[l] != 0)); 
		return;
	}
	int mid = l + r >> 1;
	if(tar <= mid)	modify(cur << 1, l, mid, tar, val);
	else	modify(cur << 1 | 1, mid + 1, r, tar, val);
	tree[cur] = min(tree[cur << 1], tree[cur << 1 | 1]);
}

int main() {
	scanf("%d%d%d", &n, &m, &t);
	for(int i = 1; i <= m; i++) {
		int u, v, w1, w2;
		scanf("%d%d%d%d", &u, &v, &w1, &w2);
		add_edge(u, v, w1);
		add_cedge(v, u, w2);
	}
	for(int i = 1; i <= n; i++)	scanf("%d", &a[i]);
	
	for(int i = 1; i <= n; i++)	dis[i] = cdis[i] = 1e18;
	
	dis[1] = 0;
	q.push(make_pair(dis[1], 1));
	while(!q.empty()) {
		int x = q.top().second;
		q.pop();
		if(vis[x])	continue;
		vis[x] = true;
		for(int i = head[x]; i; i = e[i].nxt)
			if(dis[x] + e[i].w < dis[e[i].to]) {
				dis[e[i].to] = dis[x] + e[i].w;
				q.push(make_pair(dis[e[i].to], e[i].to));
			}
	} 
	
	for(int i = 1; i <= n; i++)	vis[i] = false;
	 
	cdis[n] = 0;
	q.push(make_pair(dis[n], n));
	while(!q.empty()) {
		int x = q.top().second;
		q.pop();
		if(vis[x])	continue;
		vis[x] = true;
		for(int i = chead[x]; i; i = ce[i].nxt)
			if(cdis[x] + ce[i].w < cdis[ce[i].to]) {
				cdis[ce[i].to] = cdis[x] + ce[i].w;
				q.push(make_pair(cdis[ce[i].to], ce[i].to));
			}
	} 
	
//	for(int i = 1; i <= n; i++)	printf("点1到达点%d的距离是：%lld，点%d到达点n的距离是：%lld\n", i, dis[i], i, cdis[i]);
	build_tree(1, 1, n);
	
	for(int i = 1; i <= t; i++) {
		int x, a_;
		scanf("%d%d", &x, &a_);
		modify(1, 1, n, x, a_);
		printf("%lld\n", tree[1]);
	}
	return 0;
} 

L3-2 还原文件

一份重要文件被撕成两半，其中一半还被送进了碎纸机。我们将碎纸机里找到的纸条进行编号，如图 1 所示。然后根据断口的折线形状跟没有切碎的半张纸进行匹配，最后还原成图 2 的样子。要求你输出还原后纸条的正确拼接顺序。

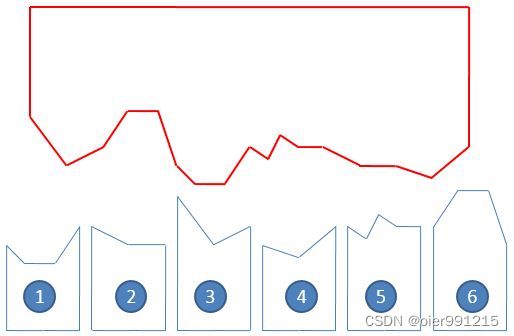
图1 纸条编号

图2 还原结果

输入格式：
输入首先在第一行中给出一个正整数 N（1

随后一行给出一个正整数 M（≤100），为碎纸机里的纸条数量。接下去有 M 行，其中第 i 行给出编号为 i（1≤i≤M）的纸条的断口信息，格式为：K h[1] h[2] … h[K]其中 K 是断口折线角点的个数（不超过 10^4+1），后面是从左到右 K 个折线角点的高度值。为简单起见，这个“高度”跟没有切碎的半张纸上断口折线角点的高度是一致的。

输出格式：
在一行中输出还原后纸条的正确拼接顺序。纸条编号间以一个空格分隔，行首尾不得有多余空格。

题目数据保证存在唯一解。

输入样例：
17
95 70 80 97 97 68 58 58 80 72 88 81 81 68 68 60 80
6
4 68 58 58 80
3 81 68 68
3 95 70 80
3 68 60 80
5 80 72 88 81 81
4 80 97 97 68
输出样例：
3 6 1 5 2 4

#include 
using namespace std;
const int Maxn = 100000 + 10;
const int Maxm = 100 + 10;
const int Maxk = 10000 + 10;
int n, m, a[Maxn], Ans[Maxm];
int s[Maxm][Maxk];
bool suc;
bool vis[Maxm];

void dfs(int now, int cur) {
	
	if(cur == m + 1) {
		suc = true;
		return;
	}
	
	for(int i = 1; i <= m && !suc; i++)
		if(vis[i] == false) {
			bool flag = true;
			for(int j = 0; j < s[i][0]; j++)
				if(a[now + j] != s[i][j + 1]) {
					flag = false;
					break;
				}
			if(flag) {
				Ans[cur] = i;
				vis[i] = true;
				dfs(now + s[i][0] - 1, cur + 1);
				vis[i] = false;
			}
		}
} 

int main() {
	
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)	scanf("%d", &a[i]);
	scanf("%d", &m);
	for(int i = 1; i <= m; i++) {
		/*
		int k;
		scanf("%d", &k);
		*/
		// s[i][j]表示第i个纸片第j个转折点的高度嘛... s[i][0]没用到，所以用来存储第i个纸片的转折点数量
		scanf("%d", &s[i][0]);
		for(int j = 1; j <= s[i][0]; j++)
			scanf("%d", &s[i][j]); 
	}
	dfs(1, 1); //当前拼到第一个转折点了，目前要找第一个纸片 
	for(int i = 1; i < m; i++)	printf("%d ", Ans[i]);
	printf("%d", Ans[m]);
	return 0;
}

L3-3 可怜的简单题

九条可怜去年出了一道题，导致一众参赛高手惨遭团灭。今年她出了一道简单题 —— 打算按照如下的方式生成一个随机的整数数列 A:

1.最开始，数列 A 为空。

2.可怜会从区间 [1,n] 中等概率随机一个整数 i 加入到数列 A 中。

3.如果不存在一个大于 1 的正整数 w，满足 A 中所有元素都是 w 的倍数，数组 A 将会作为随机生成的结果返回。否则，可怜将会返回第二步，继续增加 A 的长度。

现在，可怜告诉了你数列 n 的值，她希望你计算返回的数列 A 的期望长度。

输入格式：
输入一行两个整数 n,p (1≤n≤10^11,n

输出格式：
在一行中输出一个整数，表示答案对 p 取模的值。具体来说，假设答案的最简分数表示为x/y ，你需要输出最小的非负整数 z 满足 y×z≡x mod p。

输入样例 1：
2 998244353
输出样例 1：
2
输入样例 2：
100000000 998244353
输出样例 2：
3056898
（1分代码）

#include 
using namespace std;

int main() {
	cout << 1 << endl;
	return 0;
}

（满分代码）：大神的代码

有不懂的问题欢迎评论哦