汉诺塔问题c++递归解法

​汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

摘自百度百科 

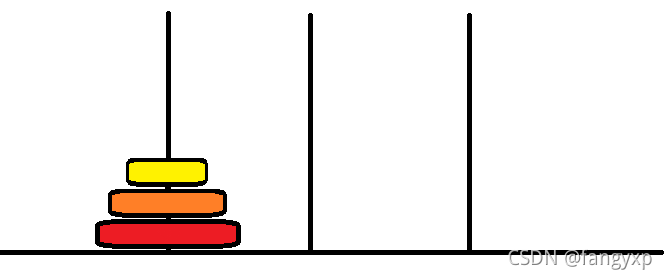
相信大家很多都玩过或者听说过汉诺塔，下面我来举个例子：（当圆盘数为3时）

目标：将所有圆盘移动至2号杆（第2根杆子） 

 

第一步：将黄色圆盘移动至2号杆上

 

 第二步：将橙色圆盘移动至3号杆上

 

 第三步：将黄色圆盘移动至3号杆上，置于橙色圆盘之上

 

第四步：将红色圆盘移动至2号杆上 

 

第五步：将黄色圆盘移动至1号杆上 

第六步：将橙色圆盘移动至2号杆上 ，置于红色圆盘之上

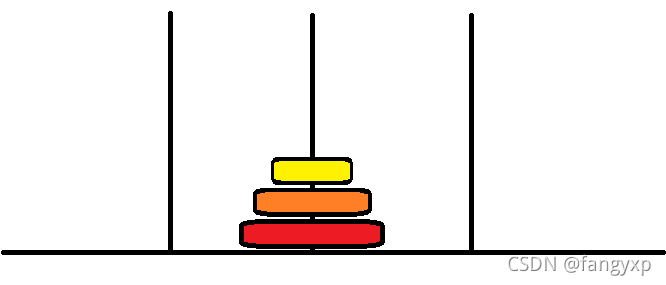
第七步：将黄色圆盘移动至2号杆上 ，置于橙色圆盘之上

至此，3圆盘的汉诺塔就已经完成了 。

从上面的图可以看出需要7步才能完成

汉诺塔步数的公式其实很简单，我再给你几个例子，你也能发现其中的规律

4层：15步

5层：31步

6层：63步

……

很明显，汉诺塔的步数公式为

步数=2的层数次方-1 

很好。

但是我只知道有多少步，我想要知道每一步是怎样走的，又该怎么办呢？

我们现在来拆分一下汉诺塔问题：

1、将最上面的圆盘移到空柱子（2选1）上

2、(       )

3、 将最后一个圆盘移到空柱子（只有1个）上

仔细思考，你会发现第2部分就是一个层数-1的汉诺塔。这意味着什么?

递归介绍

抛开这些问题不谈，我们先来聊一聊递归

首先，我想和大家讨论一个问题：什么样的数，才能算是自然数？

换种方法说：自然数的定义，是什么？

也许你会说，很简单啊，像1,2,3……这样的数叫做自然数。

但这样并不严谨。

我认为，自然数的定义分为两条：

1、0是自然数

2、比自然数大1的数，是自然数

比如我想知道3是不是自然数，我会想：

只要2是自然数，3就是自然数；

怎么判断2是不是自然数呢？

只要1是自然数，2就是自然数；

怎么判断1是不是自然数呢？

只要0是自然数，1就是自然数；

定义已经告诉我们，0是自然数，

所以1是自然数，2是自然数，3是自然数。

像这样的思考方式或技巧，被称为递归(也叫递归算法)

程序调用自身的编程技巧称为递归（ recursion）。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。

一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

摘自百度百科

上面已经告诉我们递归的意思了，但我想把它再翻译一下，让更多人能够听得懂

递归有两个部分：递归结束条件（边界条件），具体递归操作（递归前进段）

当满足递归结束条件时，递归返回，也就是return；

当不满足递归结束条件时，递归前进，也就是进行具体操作；

汉诺塔具体解法

汉诺塔问题的递归结束条件与具体递归操作如下

很简明易懂，对吧^_^

 递归问题其实很简单，只要写出递归条件，代码就很好写了

我把代码放在了这里：

#include
using namespace std;
int sum=0;//步数累加
int hanoi(int n,int a,int b,int c)
{      // 盘子数 起始1 目标3 暂存2
	if(n==1)//递归结束条件
	{
		sum++;
		cout<<"第"<> x;
	hanoi(x,1,3,2);//调用函数
	return 0;
}

运行结果：

就这样了，这是我第一次写，如果有哪里需要改正，请提出来，谢谢！