python--数据结构--二叉排序树
# search_bs_tree.py
"""
二叉排序树又称为二叉查找树,它是一种特殊的二叉树。
其定义为:二叉树排序树或者时一棵空树,或者是具有如下性质的二叉树。
(1) 若它的左子树非空,则左子树上所有结点的值均小于根结点的值。
(2) 若它的右子树非空,则右子树上所有结点的值均大于(或大于等于)根结点的值。
(3) 它的左右子树也分别为二叉排序树。
"""
from collections import deque
from matplotlib import pyplot as plt
class Node:
def __init__(self, value):
self.value = value
self.left_child = None
self.right_child = None
self.info = None
class BSTree(object):
def __init__(self, d_hor=4, d_vec=8, radius=1.5, figsize =(11, 9)):
"""
对所展示二叉树的一些元素参数的设置
:param d_hor: 节点与节点的水平距离
:param d_vec: 节点与节点的垂直距离
:param radius: 节点的半径
:param radius: 画布大小,用一个元祖表示画布width和high,单位为inch
"""
self.root = None
self.d_hor = d_hor
self.d_vec = d_vec
self.radius = radius
self.figsize = figsize
def get_left_width(self, root):
"""获得根左边宽度,也是根的左子孙节点数"""
return self.get_width(root.left_child)
def get_right_width(self, root):
"""获得根右边宽度,也是根的右子孙节点数"""
return self.get_width(root.right_child)
def get_width(self, root):
"""获得树的宽度,也是该树的节点数。使用的是中序遍历方式"""
if root:
return self.get_width(root.left_child) + 1 + self.get_width(root.right_child)
else:
return 0
def get_height(self, root):
"""获得二叉树的高度, 使用后序遍历"""
if root:
return max(self.get_height(root.left_child), self.get_height(root.right_child)) + 1
else:
return 0
def get_w_h(self, root):
"""获得树的宽度和高度"""
w = self.get_width(root)
h = self.get_height(root)
return w, h
def __draw_a_node(self, x, y, value, ax):
"""画一个节点"""
c_node = plt.Circle((x, y), radius=self.radius, color="#65DDFF")
ax.add_patch(c_node)
plt.text(x, y, value, ha='center', va='center', fontsize=25, )
def __draw_a_edge(self, x1, y1, x2, y2):
"""画一条边"""
x = (x1, x2)
y = (y1, y2)
plt.plot(x, y, 'g-')
def __create_win(self, root):
"""创建窗口"""
# WEIGHT: 树宽,HEIGHT: 树高
WEIGHT, HEIGHT = self.get_w_h(root)
# WEIGHT:树宽 + 1
WEIGHT = (WEIGHT+1)*self.d_hor
# HEIGHT = 树高+1
HEIGHT = (HEIGHT+1)*self.d_vec
# print(WEIGHT, HEIGHT)
# fig = plt.figure(figsize=(a, b), dpi=dpi)
# 设置图形的大小,a 为图形的宽, b 为图形的高,单位为英寸
# dpi 为设置图形每英寸(inch)的点数
# 1点(英美点)=0.3527毫米=1/72英寸(Office里面的点)。
# 线条,标记,文本等大多数元素都有以磅(point即点)为单位的大小。因1inch = 72point,则72dp/inch=1dp/point、144dp/inch=2dp/point
fig = plt.figure(figsize=self.figsize)
ax = fig.add_subplot(111) # 表示整个figure分成1行1列,共1个子图,这里子图在第一行第一列
plt.xlim(0, WEIGHT) # 设定x座标轴的范围,当前axes上的座标轴。
plt.ylim(0, HEIGHT) # 设定y座标轴的范围,当前axes上的座标轴。
x = (self.get_left_width(root) + 1) * self.d_hor # x, y 是第一个要绘制的节点坐标,由其左子树宽度决定
y = HEIGHT - self.d_vec
return fig, ax, x, y
def __print_tree_by_preorder(self, root, x, y, ax):
"""通过先序遍历打印二叉树"""
if not root:
# 根节点为空返回
return
# 画节点
self.__draw_a_node(x, y, root.value, ax)
# 画左右分支
lx = rx = 0
ly = ry = y - self.d_vec
if root.left_child:
lx = x - self.d_hor * (self.get_right_width(root.left_child) + 1) # x-左子树的右边宽度
self.__draw_a_edge(x, y, lx, ly)
# print(root.left_child, (lx, ly))
if root.right_child:
rx = x + self.d_hor * (self.get_left_width(root.right_child) + 1) # x-右子树的左边宽度
# print(root.right_child, (rx, ry))
self.__draw_a_edge(x, y, rx, ry)
# 递归打印
self.__print_tree_by_preorder(root.left_child, lx, ly, ax)
self.__print_tree_by_preorder(root.right_child, rx, ry, ax)
def show_BSTree_1(self):
"""可视化二叉树"""
_, ax, x, y = self.__create_win(self.root)
self.__print_tree_by_preorder(self.root, x, y, ax)
plt.show()
def insert_bst(root, key):
"""
二叉排序树的插入
问题描述:
已知一个关键字值未key的结点s,若将其插入到二叉排序书中,只要保证插入后仍符合二叉排序树的定义即可。
算法思想:
(1) 若二叉树是空树,则key成为二叉排序树的根。
(2) 若二叉排序树非空,则将key与二叉排序树的根进行比较:
a. 如果key的值等于根结点的值,则key插入左子树。
b. 如果key的值小于根结点的值,则将key插入左子树。
c. 如果key的值大于根结点的值,则将key插入右子树。
可以看出二叉排序树的插入,及插入每一个结点都是作为一个叶子节点,将其插入到二叉排序树的合适位置,插入时
不需要移动元素,不涉及树的整体移动。
算法复杂度:
时间复杂度O(log₂n)
:param root:
:param key:
:return:
"""
if not root:
root = Node(key)
elif root.value > key:
root.left_child = insert_bst(root.left_child, key) # 将key插入左子树
else:
root.right_child = insert_bst(root.right_child, key) # 将key插入右子树
return root
def create_bst(key_list: deque):
"""
创建二叉排序树
算法思想:
首先,将二叉树序树初始化为一颗空树,然后主格读入元素,每读入一个元素,就建立一个新的结点,并插入到
当前已生成的二叉排序树中,即通过多次调用二叉排序树的插入新节点的算法实现,注意插入时比较结点的顺序始终
时从二叉排序树的根节点开始。
算法时间复杂度:
假设共有n个元素,要插入n个结点需要n次插入操作,而插入一个节目的的算法时间复杂度为O(log₂n),因此创建二叉
排序树的算法时间复杂度为O(n)
log₂n
注意:
具有同样元素的序列,输入顺序不同,所创建的二叉排序树的形态不同,可见,二叉排序树的形态与元素输入顺序相关。
:param key_list: 创建二叉排序树的关键字列表
:return: 二叉排序树对象
"""
bs_tree = BSTree()
for key in key_list:
bs_tree.root = insert_bst(bs_tree.root, key)
return bs_tree
def search_bst_recursion(root, key):
"""
二叉排序树递归查找
因为二叉排序树可看作是一个有序表,所有在二叉排序树上进行查找,和折半查找类似,也是一个逐步缩小查找范围的过程。
算法思想:
首先将待查找关键字key与根结点关键字t进行比较,如果:
(1) key=t,则返回根节点地址;
(2) keyt,则进一步差右子树
算法分析:
此部分内容过多请看文章补充部分。
:param root: 已创建好的的二叉排序树的根结点
:param key: 所要查找的结点的value为key
:return: 成功返回所要查找结点,失败返回None
"""
if not root:
return None
if root.value == key:
return root # 查找成功
elif root.value > key:
return search_bst_recursion(root.left_child, key) # 在左子树继续查找
else:
return search_bst_recursion(root.right_child, key) # 在右子树继续查找
def search_bst_nonrecursion(root, key):
while root:
if root.value == key:
return root # 查找成功
elif root.value > key:
root = root.left_child # 在左子树继续查找
else:
root = root.right_child # 在右子树继续查找
def del_bst(bs_tree, key):
"""
删除二叉排序树中的指定结点
问题分析:
从二叉排序树中删除一个结点,不能把以该结点为根的子树都删去,只能删掉该结点,并且还要应保证删除后
所得的二叉树仍然满足二叉排序树的性质不变。也就是说,在二叉排序树中删去一个结点相当于删去有序序列中的
一个结点。
算法思想:
此部分内容过多请看文章补充部分。
算法分析:
显然,删除操作的基本过程是查找操作,所以其时间复杂度仍然是O(log₂n)
二叉排序树的特性:
根据二叉排序树的定义(左子树小于根结点,右子树大于根结点),根据二叉树中序遍历的定义(先中序遍历
左子树,访问根结点,在中序遍历右子树),可以得出二叉排序树的一个重要性质,即中序遍历一个二叉排序树
可以得到一个递增有序序列。
而通过你中需遍历一个二叉排序树可以得到一个递减有序序列。
:param bs_tree: 已创建好的二叉排序树
:param key: 所要删除得结点value得值为key
:return: 删除所删结点之后的二叉排序树
"""
p = bs_tree.root # 初始化当前结点
f = None # 当前结点的双亲结点
while p: # 查找关键字为key的待删结点p
if p.value == key:
break # 找到则跳出循环
elif key < p.value:
f = p # f指向p的双亲结点
p = p.left_child
else:
f = p
p = p.right_child
"""
(f, p)在此处有三种情况
(1) (not None, None) ,该二叉排序树中没有value为key的结点
(2) (None, bs_tree.root),该二叉排序树的根结点的value为key值
(3) (not None, Not None),该二叉排序树中存在value为key的结点且不是根结点
"""
if not p: # 判断该二叉排序树中没有value为key的结点
return bs_tree # 若找不到,返回原来的二叉排序树
if not p.left_child: # 判断p有无左子树
# p无左子树
if not f:
# p是原二叉排序树的根结点
bs_tree.root = p.right_child
elif p is f.left_child:
# p是f的左孩子
f.left_child = p.right_child # 将p的右子树链到f的左链上
else:
# p是f的右孩子
f.right_child = p.right_child # 将p的右子树链到f的右链上
del p # 释放被删除的结点
else:
# p有左子树,此时与p的右子树无关,该部分内容不用考虑p的右子树
q = p
s = p.left_child
while s.right_child: # 在p的左子树中查找最右下结点,条件必须使用s.right_child,不能是s
q = s
s = s.right_child
if q is p:
# p的左孩子没有右子树
q.value = s.value # 将s的value值赋给q的value,即p得value
q.left_child = s.left_child # 将s的左子树链到q的左孩子上,即p的左孩子上
else:
# p的左孩子有右子树
p.value = s.value # 将s的value值赋给p的value
q.right_child = s.left_child # 将s的左子树链到q的右孩子上
# p.value = s.value # 也可以将上面重复得两句写到该位置进行替代
del s
return bs_tree
# test_bs_tree.py
from collections import deque
from search_bs_tree import create_bst, search_bst_recursion, search_bst_nonrecursion, del_bst
if __name__ == '__main__':
# 测试create_bst
# bs_tree = create_bst(deque([5, 2, 6, 1, 4, 8, 3, 7, 9]))
# bs_tree.show_BSTree_1()
# 测试search_bst_recursion,
# bs_tree = create_bst(deque([5, 2, 6, 1, 4, 8, 3, 7, 9]))
# bs_tree.show_BSTree_1()
# search_node = search_bst_recursion(bs_tree.root, 4)
# print(search_node.value)
# search_node = search_bst_nonrecursion(bs_tree.root, 4)
# print(search_node.value)
# 测试
bs_tree = create_bst(deque([5, 2, 6, 1, 4, 8, 3, 7, 9]))
bs_tree.show_BSTree_1()
del_bst(bs_tree, 8)
bs_tree.show_BSTree_1()
补充:
(1) search_bst_recursion与search_bst_nonrecursion
算法分析:
在二叉排序树上进行查找,若查找成功,则是从根结点出发走了一条从根结点到待查节点的路径。若查找不成功,则是从根结点出发走了一条从根到某个叶子节点的路径。
二叉排序树的查找与折半查找过程类似,在二叉排序树中查找一个记录时,其比较次数不超过树的深度。但是,对长度为n的有序表而言,折半查找对应的判定树是唯一的,而含有n个结点的二叉排序树却是不唯一的,因为对于同一个关键字集合,关键字插入的先后次序不同,所构成的二叉排序树的形态和深度也不同。
而二叉排序树的平均查找长度ASL与二叉排序树的形态有关,二叉排序树的各分支越均衡,则树的深度越浅,其平均查找长度ASL越小。例如,图8.7为两颗二叉排序树,它们对应同一元素集合,单排列顺序不同,分别是(45,24, 53,12,37,93)和(12,24,37,45,53,93)。假设每个元素的查找概率相等,则它们的平均查找长度分别是:
由此可见,在二叉排序树上进行查找时的平均查找长度和二叉排序树的形态有关。在最坏情况下,二叉排序树是通过摆一个有序表的n个结点一次插入生成的,由此得到二叉排序树蜕化为一棵深度为n的单支树,它的平均查找长度和单链表上的顺序查找相同,也是(n+1)/2。在最好情况下,二叉排序树在生成过程中,树的形态毕节均与,追随得到的是一颗形态与折半查找的判定树相似的二叉排序树,此时它的平均查找长度大约为log₂n。
若考虑把n个结点,按各种可能的次序插入到二叉排序树中,则有n!棵二叉排序树(其中有的形态相同),可以证明,对这些二叉排序树的查找长度进行平均,得到的平均查找长度仍然是O(log₂n)。
就平均性能而言,二叉排序树上的查找和折半查找相差不大,平且二叉排序树上的插入和删除节点十分方便,无需移动大量结点。因此,对于需要经常作插入、删除、查找运算的表,宜采用二叉排序树结构。因此也常常将二叉排序树成为二叉查找树。
(2) def_bst算法思想
算法思想:
删除操作首先查找要删除的结点,看是否在二叉排序树中,若不在则不做任何操作;否则,假设要删除的结点为p,结点p的双亲结点为f,并假设结点p是结点f的左孩子(右孩子情况类似)。下面分三种情况讨论。
- (1) 若p为叶结点,则可直接将其删除:f→left_child = None;del(p)。
- (2) 若p结点只有左子树,或只有右子树,则可将p的左子树或右子树,直接改为其双亲结点f的左子树。即 f→left_child = p→left_child(或f→left_child = p→rchild);del(p)。
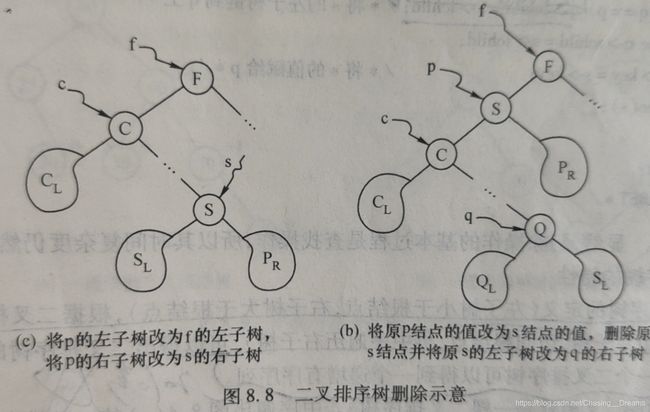
- (3) 若p既有左子树,又有右子树,如图8.8(a)所示。此时有以下两种处理方法。(图片请看补充部分)
- a. 方法1:首先找到p结点在中序序列中的直接前驱s结点,如图8.8(b)所示,然后将p的左子树改为f的左子 树,而将p的右子树改为s的右子树:f→left_child=p→left_child;s→right_child=p→right_child; del(p);如图8.8(c)所示。
- b. 方法2:首先找到p结点在中序序列中的直接前驱s结点,如图8.8(b)所示,然后用s结点代替p结点的值,再将s结点删除,原s结点的左子树改为s的双亲结点q的右子树:p→value=s→value; q→right_child=s→left_child;del(s);结果如图8.8(d)所示。