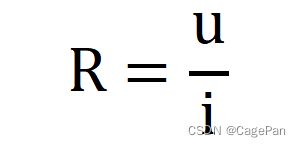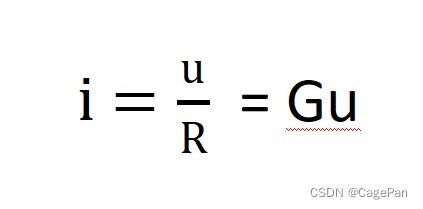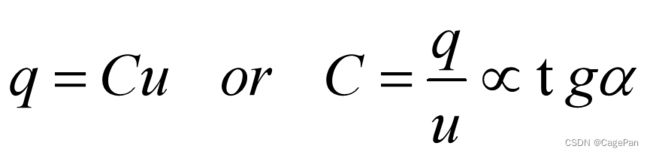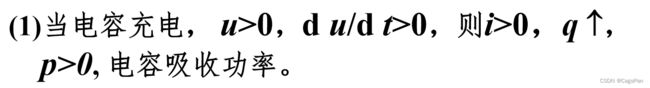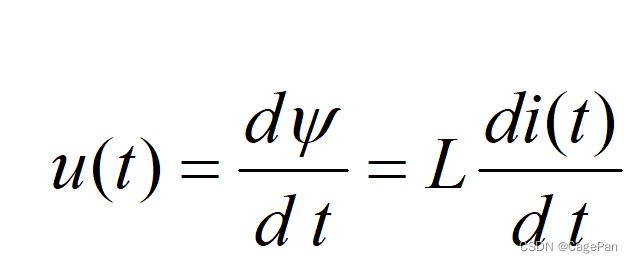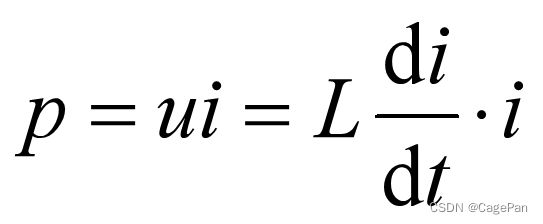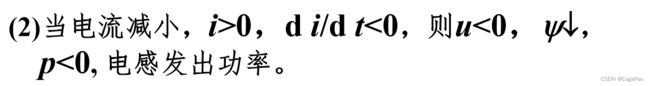电路基础元件
文章目录
- 每周电子w5——电路元件
-
- 基本电路元件
-
- 电阻元件
- 电容元件
- 电感元件
每周电子w5——电路元件
基本电路元件
电路元件:是电路中最基本的组成单元
电路元件通过其端子与外部相连接;元件的特性则通过与端子有关的物理量描述每一种元件反映某种确定的电磁性质。
集总参数电路:由集总元件构成的电路
集总元件:假定发生的电磁过程都集中在元件内部进行
三种基本电路元件:
电阻元件R:表示消耗电能的元件
电感元件L:表示产生磁场、储存磁场能量的元件
电容元件C:表示产生电场、储存电场能量的元件
电路元件的分类
按与外部连接的端子数目分为二端、三端元件等
电路元件还可分为:
有源元件和无源元件
线性元件和非线性元件
时变元件和时不变元件
电阻元件
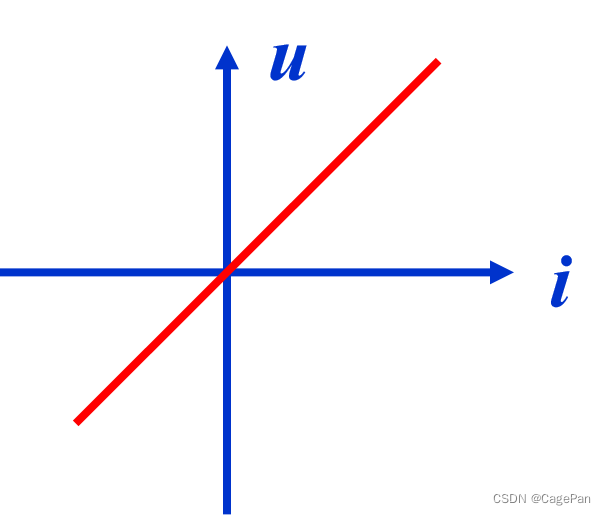
定义:对电流呈现阻力的元件。其特性可用u~i平面上的一条曲线来描述
伏安特性:
线性时不变电阻元件:任何时刻端电压与电流成正比的电阻元件
欧姆定律
R 称为电阻,单位:Ω (Ohm)
G 称为电导,单位:S (Siemens)
1.只适用于线性电阻(R为常数)
2.如电阻上的电压与电流参考方向非关联,公式中应冠以负号
3.线性电阻是无记忆、双向性的元件
电阻的功率和能量
to到t电阻消耗的能量
电阻的开路与短路
开路
i = 0
u≠0
R = ∞ G =0
短路
i ≠ 0
u = 0
R = 0 G = ∞
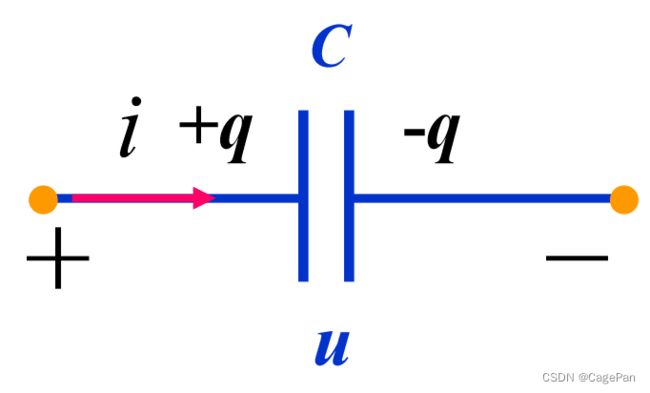
电容元件
电容元件:存储电能的元件,其特性可用u~q平面上的一条曲线来描述
电容器:在外电源作用下,两极板上分别带上等量异号电荷,撤去电源,板上电荷仍可长久地聚集下去,是一种储存电能的部件
线性定常电容元件:任何时刻,电容元件极板上的电荷q与电压u成正比
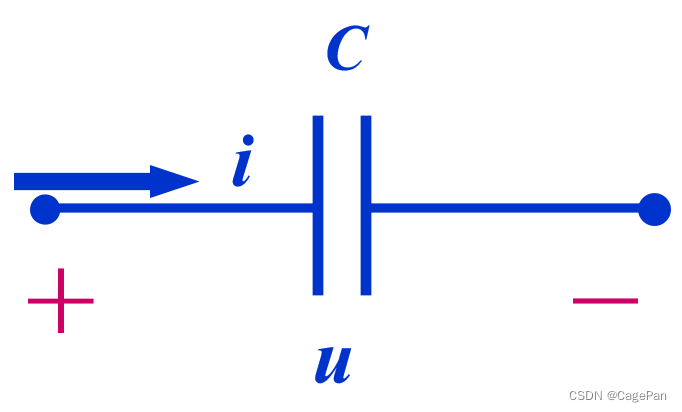
电路符号:
单位:C称为电容,单位:F(法),Farad(法拉),常用uF,pF等表示
线性电容的电压、电流关系
电容元VCR的微分关系:
1.i的大小取决于u的变化率,与u的大小无关,电容是动态元件
2.当u为常数(直流)时,i=0;电容相当于开路,电容有隔断直流作用
3.实际电路中通过电容的电流i为有限值,则电容电压必定是时间的连续函数
电容元件有记忆电压的作用,故称电容为记忆元件
1.当u,i为非关联方向时,上述微分和积分表达式前要冠以负号
2.上式中u(t0)称为电容电压的初始值,它反映电容初始时刻的储能状况,也称为初始状态
电容的功率
电容能在一段时间内吸收外部供给的能量转化为电场能量储存起来,在另一段时间内又把能量释放回电路,因此电容元件是无源元件,是储能元件,它本省不消耗能量
电流的储能
从 t0 到 t 电容储能的变化量:
1.电容的储能只与当时的电压值有关,电容电压不能跃变,反映了储能不能跃变
2.电容储存的能量一定大于或等于零
电感元件
电感元件
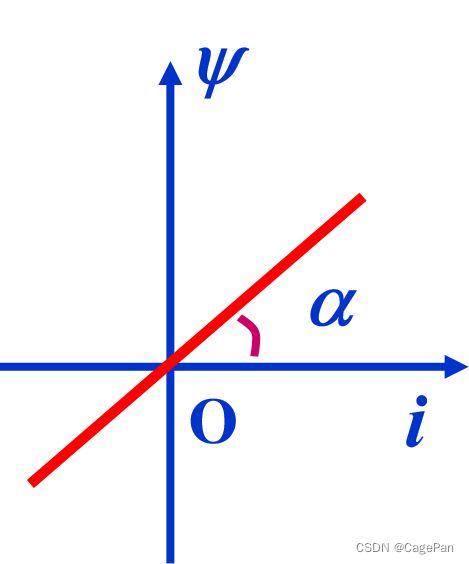
储存磁能的元件,其特性可用韦安特性w~i平面上的一条曲线来描述
电感器
把金属导线绕在一骨架上构成一实际电感器,当电流通过线圈时,将产生磁通,是一种储存磁能的部件
线性定常电感元件
任何时刻,通过电感元件的电流i 与其磁链w成正比
w~i特性是过原点的直线
单位:L 称为电感器的自感系数,L的单位: H(亨) (Henry, 亨利), 常用uH,mH表示
线性电感的电压、电流关系
根据电磁感应定律与楞次定律:
1.电感电压u的大小取决于i的变换率,与i的大小无关,电感是动态元件;
2.当i为常数(直流)时, u=0;电感相当于短路
3.实际电路中电感的电压u为有限值,则电感电流i不能跃变,必定是时间的连续函数。
电感元件VCR的积分关系
电感元件有记忆电流的作用,故称电感为记忆元件
1.当u,i为非关联方向时,上述微分和积分表达式前要冠以负号
2.上式中i(t0)称为电感电流的初始值,它反映电感初始时刻的储能状况,也称为初始状态。
电感的功率
电感能在一段时间内吸收外部供给的能量转化为磁场能量储存起来,在另一段时间内又把能量释放回电路,因此电感元件是无源元件,又是储能元件,它本身不消耗能量
电感的储能
从 t0 到 t 电容储能的变化量:
1.电感的储能只与当时的电流值有关,电感电流不能跃变,反映了储能不能跃变
2.电感储存的能量一定大于或等于零