计算机网络课后作业2023秋
计算机网络第三版吴功宜版 课后作业
- 第一章作业
-
- 三、计算与问答
-
- 3.7
- 3.8
- 第二章作业
-
- 三、计算与问答
-
- 3.2
- 3.5
- 3.6
- 第三章作业
-
- 三、计算与问答
-
- 3.1
- 3.5
- 3.7
- 3.8
- 第四章作业
-
- 三、计算与问答
-
- 3.1
- 3.2
- 第五章作业
-
- 三、计算与问答
-
- 3.1
- 3.3
- 3.4
- VLAN
-
- 交换机模式
- 模式切换
- 重置交换机
- VLAN配置命令
- 其它命令
第一章作业
三、计算与问答
3.7
- 长度为 8B与536B 的应用层数据通过传输层时加上了 20B的 TCP 报头,通过网络层时加上60B的IP分组头通过数据链路层时加上了18B的 Ethernet 头和尾。分别计算两种情况下的数据传输效率。
8B: 8 8 + 20 + 60 + 18 = 4 53 ≈ 0.0755 \frac{8}{8+20+60+18}=\frac{4}{53} \approx 0.0755 8+20+60+188=534≈0.0755
536B: 536 536 + 20 + 60 + 18 = 536 634 ≈ 0.845 \frac{536}{536+20+60+18}=\frac{536}{634} \approx 0.845 536+20+60+18536=634536≈0.845
3.8
- 计算发送延时与传播延时条件:
主机之间传输介质长度 D=1000km。电磁波传播速度为 2 × 1 0 8 2\times10^8 2×108m/s。
(1) 数据长度为 1 × 1 0 3 1\times10^3 1×103bit,数据发送速率为100Kbps。
(2) 数据长度为 1 × 1 0 8 1\times10^8 1×108bit,数据发送速率为10Gbps。
(1)
数据长度:N= 1 × 1 0 3 1\times10^3 1×103bit
数据发送速率:S=100Kbps
发送延时 T = N S = 1 0 3 100 × 1 0 3 = 1 100 s \mathrm{T}=\frac{N}{S}=\frac{10^3}{100\times 10^3}=\frac{1}{100}\mathrm{s} T=SN=100×103103=1001s
传播距离:D=1000km
传播速度:V= 2 × 1 0 8 2\times10^8 2×108m/s
传播时间: T = D V = 1000 × 1 0 3 2 × 1 0 8 = 1 200 T = \frac{D}{V}=\frac{1000\times 10^3}{2\times10^8}=\frac{1}{200} T=VD=2×1081000×103=2001s
(2)
发送延时 T = N S = 1 0 8 10 × 1 0 9 = 1 100 s \mathrm{T}=\frac{N}{S}=\frac{10^8}{10\times 10^9}=\frac{1}{100}\mathrm{s} T=SN=10×109108=1001s
传播时间: T = D V = 1000 × 1 0 3 2 × 1 0 8 = 1 200 T = \frac{D}{V}=\frac{1000\times 10^3}{2\times10^8}=\frac{1}{200} T=VD=2×1081000×103=2001s
第二章作业
三、计算与问答
3.2
- 计算机网络采用层次结构的模型有什么好处?
3.5
- 请描述在 OSI 参考模型中数据传输的基本过程。
3.6
- TCP/IP的主要特点是什么?
第三章作业
三、计算与问答
3.1
- 已知:电话线路带宽B=3000Hz,根据奎斯特准则求无噪声信道的最大数据传输速率为多少?
参考教材 P85
根据奈奎斯特定理,二进制数据信号的最大传输速率 R m a x R_{max} Rmax与理想信道带宽 B B B(单位 H z \mathrm{Hz} Hz)的关系可以写为 R m a x = 2 B ( b p s ) R_{max}=2B(bps) Rmax=2B(bps).
B = 3000 H z \mathrm{B}=3000Hz B=3000Hz
R m a x = 2 B = 2 × 3000 = 6000 b p s R_{max}=2B=2\times 3000=6000\;bps Rmax=2B=2×3000=6000bps
3.5
参考教材 P80
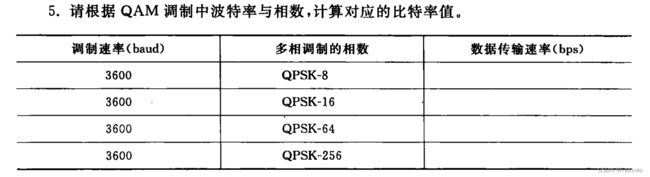
比特率S(单位为bps)与调制速率B(单位为baud)之间的关系可以表示为: S = B ⋅ l o g 2 k S=B\cdot\mathrm{log}_2k S=B⋅log2k。 k k k为多相调制的相数, l o g 2 k \mathrm{log}_2k log2k值表示一次调制转态的变化传输的二进制比特数。
| 调制速率:B(baud) | 多相调制的相数: l o g 2 k \mathrm{log}_2k log2k | 数据传输速率:S(bps) |
|---|---|---|
| 3600 | QPSK-8 ( l o g 2 8 = 3 ) (\mathrm{log}_28=3) (log28=3) | 3600 × 3 = 10800 3600\times 3=10800 3600×3=10800 |
| 3600 | QPSK-16 ( l o g 2 16 = 4 ) (\mathrm{log}_216=4) (log216=4) | 3600 × 4 = 14400 3600\times 4=14400 3600×4=14400 |
| 3600 | QPSK-64 ( l o g 2 64 = 6 ) (\mathrm{log}_264=6) (log264=6) | 3600 × 6 = 21600 3600\times 6=21600 3600×6=21600 |
| 3600 | QPSK-256 ( l o g 2 256 = 8 ) (\mathrm{log}_2256=8) (log2256=8) | 3600 × 8 = 28800 3600\times 8=28800 3600×8=28800 |
3.7
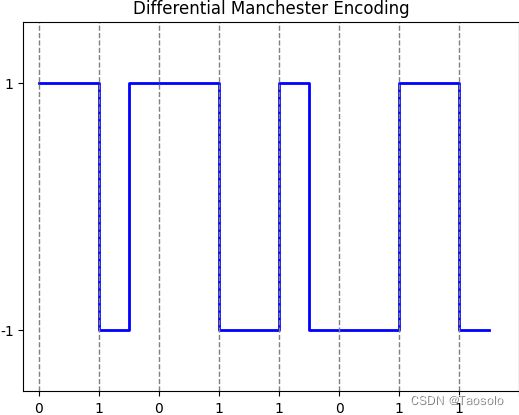
- 已知:A=01011011。请画出A的差分曼彻斯特编码的波形
Online python: Python compiler: link
如果自己机器上没有Python环境,可以用在线Python解析器来运行下面的代码
# 绘制差分曼彻斯特编码code
# 定义一个函数,接受一个二进制字符串作为参数,返回一个差分曼彻斯特编码的波形图
# 导入matplotlib库,用来绘制波形图
import matplotlib.pyplot as plt
def diff_manchester(binary_string, level=-1):
# 初始化一个空列表,用来存储编码后的电平值
levels = []
# 初始化一个变量,用来记录当前的电频,默认初始电平为-1,表示低电频
level = level
# 遍历二进制字符串中的每个比特
for bit in binary_string:
# 如果比特为0,那么在比特周期的开始处电平跳变,中间保持不变
if bit == "0":
level = -level # 电平跳变
levels.append(level) # 添加到列表中
levels.append(level) # 添加到列表中
# 如果比特为1,那么在比特周期的开始处电平保持不变,中间跳变
else:
levels.append(level) # 添加到列表中
level = -level # 电平跳变
levels.append(level) # 添加到列表中
# 设置x轴的刻度,每个比特占两个单位
xticks = [i for i in range(0, len(binary_string) * 2 + 1, 2)]
# 设置x轴的标签,显示原始的二进制字符串
xlabels = list(binary_string)
# 在xlabels列表的末尾添加一个空字符串,使其长度与xticks相同
xlabels.append("")
# 创建一个新的图形
plt.figure()
# 绘制折线图,使用阶梯状的线条,颜色为蓝色,线宽为2
plt.plot(levels, drawstyle="steps-pre", color="blue", linewidth=2)
# 设置x轴的范围,从-0.5到最后一个比特的中间
plt.xlim(-0.5, len(binary_string) * 2 - 0.5)
# 设置y轴的范围,从-1.5到1.5
plt.ylim(-1.5, 1.5)
# 设置x轴的刻度和标签
plt.xticks(xticks, xlabels)
# 设置y轴的刻度和标签,只显示-1和1
plt.yticks([-1, 1], [-1, 1])
# 设置标题,显示差分曼彻斯特编码
plt.title("Differential Manchester Encoding")
# 遍历每个比特周期的开始处
for i in range(0, len(binary_string) * 2, 2):
# 绘制一条从-1.5到1.5的竖着的虚线,颜色为灰色,线宽为1
plt.vlines(i, -1.5, 1.5, linestyles="dashed", color="gray", linewidth=1)
# 显示图形
plt.show()
# test
diff_manchester('01011011')
3.8
- 如果主机的数据发送速率达到 100Mbps,采用曼彻斯特编码,那么相应的时钟频率应该为多少?
第四章作业
三、计算与问答
3.1
- 如果数据字段为11100011,生成多项式 G ( X ) = X 5 + X 4 + X + 1 G(X)=X^5+X^4+X+1 G(X)=X5+X4+X+1。请写出发送的比特序列,并画出曼彻斯特编码序号波形图。
参考教材:P108
参考视频链接
模二运算除法在线工具
G ( X ) G(X) G(X)展开式: G ( X ) = 1 × X 5 + 1 × X 4 + 0 × X 3 + 0 × X 2 + 1 × X 1 + 1 × X 0 G(X)=1\times X^5+1\times X^4+0\times X^3+0\times X^2+1\times X^1+1\times X^0 G(X)=1×X5+1×X4+0×X3+0×X2+1×X1+1×X0
G ( X ) G(X) G(X)展开式的系数,既多项式比特序列: 1 1 0 0 1 1 1\;1\;0\;0\;1\;1 110011
f ( x ) f(x) f(x)数据字段: 1 1 1 0 0 0 1 1 1\;1\;1\;0\;0\;0\;1\;1 11100011
多项式的系数序列的长度: N = 6 N=6 N=6
余数的长度 k k k为多项式的系数序列的长度 N − 1 N-1 N−1: k = N − 1 ; e . g . , 6 − 1 = 5 k=N-1;\;e.g.,6-1=5 k=N−1;e.g.,6−1=5
余数的长度: k = 5 k=5 k=5
在数据字段后面增加k个0,用来保证够除以多项式比特序列,得到被除数: 1 1 1 0 0 0 1 1 0 0 0 0 0 1\;1\;1\;0\;0\;0\;1\;1\;0\;0\;0\;0\;0 1110001100000
用多项式比特序列: 1 1 0 0 1 1 1\;1\;0\;0\;1\;1 110011作为除数, 1 1 1 0 0 0 1 1 0 0 0 0 0 1\;1\;1\;0\;0\;0\;1\;1\;0\;0\;0\;0\;0 1110001100000作为被除数,求余数,然后把余数加到被除数即可得到增加了CRC冗余码的传输比特流。
答案: 1 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 1 0 1\;1\;1\;0\;0\;0\;1\;1\;0\;0\;0\;0\;0\;1\;1\;0\;1\;0 111000110000011010
计算过程:
(1) 求余数
求得余数为: 1 1 0 1 0 1\;1\;0\;1\;0 11010
(2) 求传输比特流
发送比特序列=被除数+余数
发送比特序列 = 1 1 1 0 0 0 1 1 0 0 0 0 0 + 1 1 0 1 0 = 1 1 1 0 0 0 1 1 1 1 0 1 0 1\;1\;1\;0\;0\;0\;1\;1\;0\;0\;0\;0\;0+1\;1\;0\;1\;0=1\;1\;1\;0\;0\;0\;1\;1\;1\;1\;0\;1\;0 1110001100000+11010=1110001111010
Online python: Python compiler: link
如果自己机器上没有Python环境,可以用在线Python解析器来运行下面的代码
# 绘制曼彻斯特编码波形code
# 导入matplotlib库
import matplotlib.pyplot as plt
# 定义一个函数,输入任意二进制比特流,绘制出曼彻斯特编码图
def manchester_encoding(bitstream):
# 初始化曼彻斯特编码的列表
manchester = []
# 遍历输入的比特流
for bit in bitstream:
# 如果当前比特是0,曼彻斯特编码为01
if bit == '0':
manchester.extend([0, 1])
# 如果当前比特是1,曼彻斯特编码为10
elif bit == '1':
manchester.extend([1, 0])
# 反转曼彻斯特编码的列表,让0用低电平表示,1用高电平表示
manchester = [1 - x for x in manchester]
# 绘制曼彻斯特编码的图
plt.figure(figsize=(5, 3))
plt.step(range(len(manchester)), manchester, where='post')
plt.title('Manchester encoding of ' + bitstream)
plt.xlabel('Time')
plt.ylabel('Level')
plt.yticks([0, 1])
plt.tight_layout()
plt.show()
# 测试函数
manchester_encoding('1110001111010')
3.2
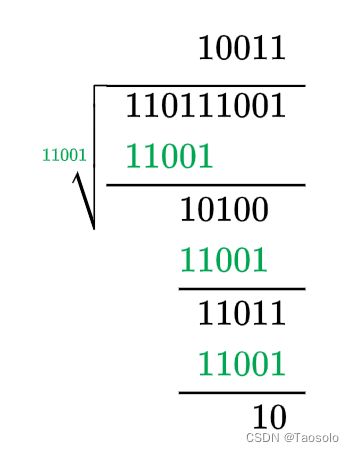
- 某个数据通信系统采用 CRC校验方式,并且生成多项式 G ( x ) G(x) G(x)的二进制比特序列为11001,目的主机接收到的二进制比特序列为 110111001(含 CRC 校验码)。请判断传输过程中是否出现了差错?为什么?
答案:出错,因为除不尽呀
参考教材 P108
CRC的校验原理为:
发送方
被除数=二进制比特序列
除数=原始数据+二进制比特序列长度-1个0
余数=除数 ÷ {\div} ÷被除数
发送数据=除数+余数
接收方
用接收到的数据 ÷ \div ÷被除数,如果余数为0则认为没有错误,否则有错
需要说明的是:被除数是提前约定好的,两方都是在协议里提前说好的
计算过程:
接收到的数据 ÷ \div ÷除数 ≠ 0 \ne 0 =0,所以数据在传输过程中发生错误。
第五章作业
三、计算与问答
3.1
- 采用CSMA/CD介质访问控制方式的局域网,总线长度为 1000m,数据传输速率为10Mbps,电磁波在总线传输介质中的传播速度为 2 × 1 0 8 2\times10^8 2×108m/s。计算:最小帧长度应该为多少?
参考教材p146
最短帧长度: L m i n L_{min} Lmin
主机发送速率: S S S
主机发送的数据帧最短帧长=争用期时长×数据传输速率: L m i n = 2 τ × V L_{min}=2\tau\times V Lmin=2τ×V。
传输延迟=总线长度/传播速度,既: τ = D / V \tau=D/V τ=D/V
其中争用期为端到端传输时延的两倍 : T c = 2 τ T_c = 2\tau Tc=2τ
如果发生主机发送信号后出现冲突则在 2 τ 2\tau 2τ时间内必能检测到并停止发送,如果发送信息的时间短于争用期,则在检测到冲突之前信息就已经发送完毕,所以发送数据帧的时间应长于争用期。
既要满足关系: L m i n S ≥ T c \frac{L_{min}}{S}\ge T_c SLmin≥Tc
D=1000
V = 2 × 1 0 8 2\times10^8 2×108
S = 10Mbps
τ = D V = 1000 2 × 1 0 8 = 0.5 × 1 0 − 5 \tau=\frac{D}{V}=\frac{1000}{2\times10^8}=0.5\times10^{-5} τ=VD=2×1081000=0.5×10−5
T c = 2 τ = 2 × 0.5 × 1 0 − 5 = 1 0 − 5 T_c=2\tau=2\times0.5\times10^{-5}=10^{-5} Tc=2τ=2×0.5×10−5=10−5
L m i n = T c × S = 1 0 5 × 10 M b p s = 1 0 − 5 × 10 × 1 0 6 b p s = 100 L_{min}=T_c\times S =10^{5}\times10\mathrm{Mbps}=10^{-5}\times 10\times 10^{6}\mathrm{bps}=100 Lmin=Tc×S=105×10Mbps=10−5×10×106bps=100bit
3.3
3.主机A 连接在总线长度为 1000m 的局域网总线的一端,局域网介质访控制方式为CSMA/CD,发送速率为100Mbps。电磁波在总线传输介质中的传播速度为 2 × 1 0 8 2\times10^8 2×108m/s。如果主机 A 最先发送帧,并且在检测出冲突发生的时候还有数据要发送。请回答:
(1)主机A 检测到冲突需要多长时间?
(2)当检测到冲突的时候,主机 A 已经发送多少位的数据?
(1)
D=1000
V= 2 × 1 0 8 2\times10^8 2×108
τ = D V = 1000 2 × 1 0 8 = 0.5 × 1 0 − 5 \tau=\frac{D}{V}=\frac{1000}{2\times10^8}=0.5\times10^{-5} τ=VD=2×1081000=0.5×10−5s
T c = 2 τ = 2 × 0.5 × 1 0 − 5 = 1 0 − 5 T_c = 2\tau=2\times0.5\times10^{-5}=10^{-5} Tc=2τ=2×0.5×10−5=10−5s=10 μ \mu μs
(2)
S=100Mbps= 100 × 1 0 6 100\times 10^6 100×106bps
L m i n = S × T c = 100 × 1 0 6 × 1 0 − 5 = 1000 L_{min}=S\times T_c=100\times 10^6\times10^{-5}=1000 Lmin=S×Tc=100×106×10−5=1000bit
3.4
- 采用 CSMA/CD介质访问控制方式的局域网,总线长度为 2000m,数据传输速率为10Mbps,电磁波在总线传输介质中的传播速度为 2 × 1 0 8 2\times10^8 2×108m/s。
假设:局域网中主机A 与主机 B连接在总线的两端并且只有主机 A、B发送数据。请回答:
(1)如果发送数据后发生冲突,那么从开始发送数据到检测到冲突,最短需要多少时间?最长需要多少时间?
(2)如果局域网中不存在冲突,主机A发送一个最长 Ethernet 帧(1518B)之后,主机B就用一个最短 Ethernet帧 (64B)确认。主机 A在得到确认之后就立即发送下一帧。忽略帧间间隔,那么主机 A的有效传输速率是多少?
(1)
最短时间( T 1 T_1 T1):既主机A和主机B同时开始发送数据的情况下,那么他们会在传输过程中检测到冲突的时间。
最长时间( T 2 T_2 T2):就是一个先发,数据刚要到另一个机器的时候,另一个机器开始发,比如主机A在检测到总线空闲后开始发送数据,而主机B在主机A的数据到达之前的一瞬间也开始发送数据,那么他们会在主机B的数据到达主机A处时检测到冲突。
显然最长时间是最短时间的两倍既: T 2 = 2 T 1 T_2=2T_1 T2=2T1
D=2000
V= 2 × 1 0 8 2\times10^8 2×108
S=10Mbps= 10 × 1 0 6 10\times 10^6 10×106bps
T 1 = D V = 2000 2 × 1 0 8 = 1 × 1 0 − 5 s = 10 μ T_1=\frac{D}{V}=\frac{2000}{2\times10^8}=1\times10^{-5}\mathrm{s}=10\mu T1=VD=2×1082000=1×10−5s=10μs
T 2 = 2 T 1 = 20 μ T_2 = 2T_1=20\mu T2=2T1=20μs
(2)
有效传输速率:如果局域网中不存在冲突,那么主机A发送一个最长 Ethernet 帧(1518B)的时间为 T 3 T_3 T3
T 3 = 1518 B × 8 b i t 10 M b p s = 1.2144 × 1 0 − 3 s = 1.2144 m s T_3=\frac{1518 \mathrm{~B} \times 8 \mathrm{bit}}{10 \mathrm{Mbps}}=1.2144\times10^{-3}\mathrm{s}=1.2144 \mathrm{~ms} T3=10Mbps1518 B×8bit=1.2144×10−3s=1.2144 ms
主机B收到主机A的帧后,立即发送一个最短 Ethernet 帧 (64B)作为确认,其发送时间为 T 4 T_4 T4
T 4 = 64 B × 8 b i t 10 M b p s = 0.0512 × 1 0 − 3 s = 0.0512 m s T_{4}=\frac{64 \mathrm{~B} \times 8 \mathrm{bit}}{10 \mathrm{Mbps}}=0.0512\times 10^{-3}\mathrm{s}=0.0512 \mathrm{~ms} T4=10Mbps64 B×8bit=0.0512×10−3s=0.0512 ms
主机A收到主机B的确认后,立即发送下一帧,那么主机A发送两个最长 Ethernet 帧的时间间隔,既发送一个帧到在发送下一个帧的时间为 T 5 T_5 T5
T 5 = T 3 + 2 × T 1 + T 4 = 1.2865 × 1 0 − 3 s = 1.2865 m s T_5=T_3+2\times T_1+T_4=1.2865\times10^{-3}\mathrm{s}=1.2865ms T5=T3+2×T1+T4=1.2865×10−3s=1.2865ms
其中, T 1 T_1 T1为主机A、B之间帧的传输时间,2倍 T 1 T_1 T1表示A传给B,B的确认信息又传给A。
在计算主机A发送一个完整的最长 Ethernet 帧的有效传输速率时,只考虑帧中的有效数据,既去除帧头的18B
r = ( 1518 − 18 ) B × 8 b i t T 5 ≈ 9.33 M b p s r=\frac{(1518-18) B \times 8 b i t}{T_{5}}\approx 9.33 \mathrm{Mbps} r=T5(1518−18)B×8bit≈9.33Mbps
VLAN
交换机模式
Switch> 用户模式,可以查看信息,不能修改配置,默认入口
Switch# (enable)特权模式,可以查看信息,可以执行管理命令,如重启,备份,重置等
Switch(config)# (conf t)全局配置模式,可以修改交换机的全局配置,比如主机名,密码,IP
Switch(config-if)# (interface FastEthernet0/1)接口配置模式,可以修改各个接口的配置,VLAN编号,名称等
模式切换
从用户模式进入特权模式:输入enable命令,然后输入密码。
从特权模式进入全局配置模式:输入configure terminal命令。
从全局配置模式进入接口配置模式:输入interface命令,然后输入接口编号。
从全局配置模式进入VLAN配置模式:输入vlan database命令。
从任何模式返回上一级模式:输入exit命令。
从任何模式返回用户模式:输入end命令。
在全局配置模式下执行特权模式的命令:在命令前加do关键字。
重置交换机
enable: 进入特权模式
erase startup-config:重置配置文件
reload:重启交换机
VLAN配置命令
Switch>enable # 进入特权模式
Switch#show vlan # 查看vlan
Switch#conf t # 进入全局配置模式
Switch(config)#vlan 10 # 全局模式下创建VLAN编号
Switch(config-vlan)#name VLAN10 # VLAN 配置模式
Switch(config-vlan)#exit # 退出VLAN配置模式到全局配置模式
Switch(config)#do show vlan # 全局配置模式下查看VLAN信息
Switch(config)#no vlan 10 # 全局模式下清除VLAN
Switch(config)#interface FastEthernet0/1 #进入交换机端口1
Switch(config)#interface FastEthernet0/1 #配置端口1的模式为access,access表示该端口只允许一个VLAN数据通过
Switch(config-if)#switchport access vlan 10 #配置端口2属于vlan 10
Switch(config-if)#exit 退出端口1
Switch(config-if)#switchport mode trunk #配置端口类型为trunk模式,trunk模式运行多个VLAN的数据通过该端口
其它命令
ping ip #测试网络是否畅通
arp -a #查看可到达的ip-mac 地址表
ipconfig -all # 查看网络配置信息
netsh interface ip set address name=“本地连接” source=static addr=192.168.0.3 mask=255.255.255.0 gateway=192.168.0.1 gwmetric=auto(gateway和gwmetric默认不设置也可以)