Day24 力扣回溯 : 491.递增子序列 |46.全排列 |47.全排列 II
Day24 力扣回溯 : 491.递增子序列 |46.全排列 |47.全排列 II
- 491.递增子序列
- 46.全排列
- 47.全排列 II
491.递增子序列
本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。
https://programmercarl.com/0491.%E9%80%92%E5%A2%9E%E5%AD%90%E5%BA%8F%E5%88%97.html视频讲解:https://www.bilibili.com/video/BV1EG4y1h78v
第一印象:
确实像,这道题首先不能排序。就需要保证,每次往path里add的时候,这个数是比path里最后一个数字 >= 的。我先试试
其中 4677 ,47 47算做重复答案。答案至少两个数字
收集的过程我想的出来,比如44325,先拿了4,剩下4325,for循环里就挨个看,>=4的才会add,否则就不要递归。这样就能获得递增的子序列。
但是难在怎么去重,之前都是排序之后用index来去重,但是这道题不能排序,就会出现 4345 的情况,这两个45 就没法去重。。。
看看题解吧。
看完题解的思路:
我的思路是对的,只是不会去重,去重是同一树层上去重。
用set记录,一个for循环里取过的数字就可以了,就这么去重。
实现中的困难:
同一树层有两种情况不要加入path
- 这个数字没path最后的数字大
- 这个数字已经加过了(在hashset里)
if (!path.isEmpty()
&& path.get(path.size() - 1) > nums[i]
|| hash.contains(nums[i])) {
continue;
}
比如4325,选了4剩下325, 3没有4大,所以不行。但是剩下的25也要看,所以是continue,而不是break。
关于hashset为什么不回溯,因为一个for循环要新声明一个set,set只管一个for循环内出现了哪些数,不需要回溯到上面去。
我觉得就是全局变量,或者函数参数里的东西,这种很全局的是要回溯的,局部的只管一个for循环里的,不需要回溯。
感悟:
class Solution {
LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> findSubsequences(int[] nums) {
backtracking(nums, 0);
return result;
}
private void backtracking(int[] nums, int startIndex) {
if (path.size() >= 2) {
result.add(new ArrayList<>(path));
}
HashSet<Integer> hash = new HashSet<>();
for (int i = startIndex; i < nums.length; i++) {
if (!path.isEmpty() && path.get(path.size() - 1) > nums[i] || hash.contains(nums[i])) {
continue;
}
path.add(nums[i]);
hash.add(nums[i]);
backtracking(nums, i + 1);
path.removeLast();
}
}
}
46.全排列
本题重点感受一下,排列问题 与 组合问题,组合总和,子集问题的区别。 为什么排列问题不用 startIndex
https://programmercarl.com/0046.%E5%85%A8%E6%8E%92%E5%88%97.html
视频讲解:https://www.bilibili.com/video/BV19v4y1S79W
第一印象:
问题来到排列了,我直接看一手题解学习一下。
看完题解的思路:
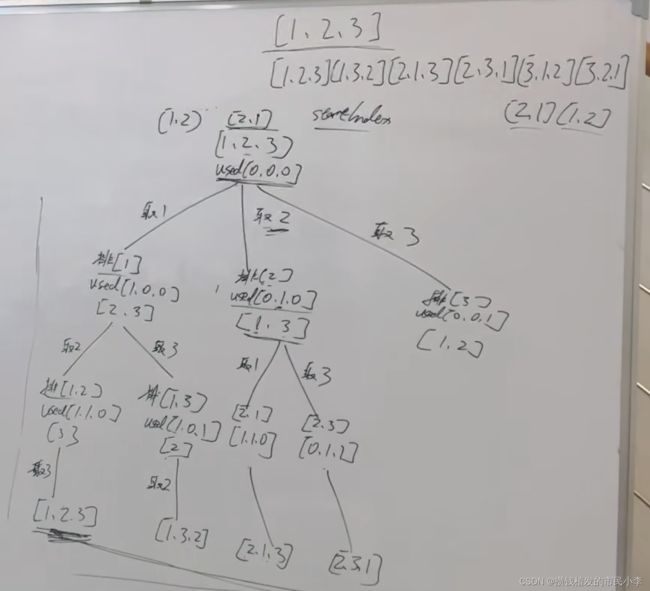
树是这样的。
排列就必须要用used数组来标记哪些元素用过了。
看图里,如果是组合,取2之后,就不要再去看1了,因为取1的地方会有12,如果取了2 再去看1,就会有21。 12 ,21 就是重复的。
但是排列不同,取了12,也要取21. 所以在排列里,每次for循环都要从数组的头重新来,而不是startIndex来去重了。
但是呢,不管排列还是组合,都不能重复使用这个2,不能有 22 的情况啊。就要标记这个2是不是用过的。for 循环每次都从头来,遇到标记用过的(used数组)元素,就跳过去(continue)就可以了。
参数返回值:
返回值回溯void,参数要有nums数组,也要有used数组。used数组是一个全局的变量,要参与回溯的过程。
private void backtracking(int[] nums, int[] used) {
终止条件:
看图, 因为是全排列,所以收集的都是树的叶子节点,也就是path的size是3的时候。
//终止条件
if (path.size() == nums.length) {
result.add(new ArrayList(path));
return;
}
单侧递归逻辑:
从nums数组的头开始遍历,遇到用过的数字就跳过。
否则,就加入path,标记为用过的,递归,回溯。
//单层递归逻辑
for (int i = 0; i < nums.length; i++) {
//如果这个数用过了,就跳过
if (used[i] == 1) {
continue;
}
path.add(nums[i]);
used[i] = 1;
backtracking(nums, used);
path.removeLast();
used[i] = 0;
}
实现遇到的困难:
按回溯模板写没有困难
感悟:
学会了排列的思路,如果不是全排列的话,也应该只是收集节点的时候不一样。
代码:
class Solution {
LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
int[] used = new int[nums.length];
backtracking(nums, used);
return result;
}
private void backtracking(int[] nums, int[] used) {
//终止条件
if (path.size() == nums.length) {
result.add(new ArrayList(path));
return;
}
//单层递归逻辑
for (int i = 0; i < nums.length; i++) {
//如果这个数用过了,就跳过
if (used[i] == 1) {
continue;
}
path.add(nums[i]);
used[i] = 1;
backtracking(nums, used);
path.removeLast();
used[i] = 0;
}
}
}
47.全排列 II
本题 就是我们讲过的 40.组合总和II 去重逻辑 和 46.全排列 的结合,可以先自己做一下,然后重点看一下 文章中 我讲的拓展内容。
used[i - 1] == true 也行,used[i - 1] == false 也行https://programmercarl.com/0047.%E5%85%A8%E6%8E%92%E5%88%97II.html
视频讲解:https://www.bilibili.com/video/BV1R84y1i7Tm
第一印象:
感觉就是index去重 + 排列的实现。我试试来.
不能用index去重,因为排列不传入startIndex。还是去思考同一树层不能重复元素,那么就是set去重了。
看完题解的思路:
题解直接用used数组去判断了,我学习一下,但我觉得我这么做很清晰,不绕圈,就是多声明一个HashSet罢了。
题解里是这么做的⬇️
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
确实,比如112的情况,选了1之后同一树枝可以再选1,只有同一树层的1是要去重的。
比如112,就不能选第二个 1 了。这种情况,used数组是[0 1 0],所以只有相邻两个一样,而且前一个还没用的时候跳过。像第一种说的情况[ 1 0 0],第一个用了,所以不用跳过也就是不用去重。
但是题解又说可以写成:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
continue;
}
说这种情况是对同一树枝的重复情况去重,我觉得这个情况很怪,确实,题解说他效率很低。而且我之前学的也是同一树层去重呀
理解一下为什么可以吧
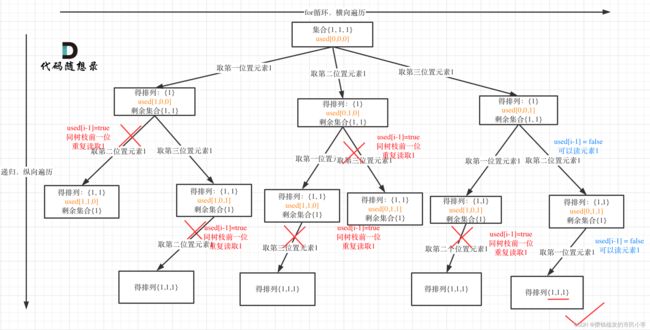
树层上去重(used[i - 1] == false),的树形结构如下:
树枝上去重(used[i - 1] == true)的树型结构如下:
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
同一树枝去重怪怪的…………别寻思了。
实现的困难:
我一开始用startIndex那样没做出来,不能排序后判断相邻的是否重复,比如112, 选完1 剩下12. 没有变量去标记这次从12 的 1开始了。如果硬弄个index去标记,因为每次都从nums头重新来,我感觉很混乱,捋不清应该传给index多少呢。i 还是i+1? 不如set来的简单了。
主要是同树层不能重复元素
感悟:
我自己还能做出来挺好的。
代码:
class Solution {
LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
int[] used = new int[nums.length];
Arrays.sort(nums);
backtracking(nums, used);
return result;
}
private void backtracking(int[] nums, int[] used) {
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
return;
}
HashSet<Integer> set = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
if (used[i] == 1) continue;
if (set.contains(nums[i])) continue;
path.add(nums[i]);
used[i] = 1;
set.add(nums[i]);
backtracking(nums, used);
path.removeLast();
used[i] = 0;
}
}
}