【机器学习/数据分析大项目】黑色星期五销售预测（详细报告）

一、项目背景

  黑色星期五是美国感恩节后的星期五，通常被称为黑色星期五。感恩节在每年11月的第四个星期四庆祝。自1952年起，感恩节后的第二天被视为美国圣诞购物季的开始，尽管直到最近几十年，"黑色星期五"这个术语才变得广泛使用。许多商店在黑色星期五提供大力推广的促销活动，非常早就开门，比如午夜，甚至可能在感恩节当天就开始销售。对于零售店或电子商务企业来说，最大的挑战是选择产品价格，以便在销售结束时获得最大利润。我们的项目涉及根据历史零售店销售数据确定产品价格。在生成预测之后，我们的模型将帮助零售店确定产品的价格以获取更多利润。

二、问题描述

  一家零售公司希望了解顾客在不同类别的各种产品上的购买行为（具体来说，购买金额）。他们分享了上个月各个高销量产品的顾客购买摘要。数据集还包含顾客的人口统计信息（年龄、性别、婚姻状况、城市类型、停留在当前城市的时间）、产品详情（产品ID和产品类别）以及上个月的总购买金额。
  现在，他们希望构建一个模型来预测顾客在各种产品上的购买金额，这将帮助他们为不同产品制定个性化的优惠。

三、数据集描述

  本项目采用的数据集是通过Analytics Vidhya主办的在线数据分析黑客马拉松获得的。数据包含年龄、性别、婚姻状况、购买的产品类别、城市人口统计信息、购买金额等特征。该数据集共有12列和537,577条记录。我们的模型将通过训练该数据集来预测产品的购买金额。
  您可以通过下面百度网盘链接下载项目所需的数据集：数据集下载链接

  数据集具体变量定义如下：
   • User_ID: 用户ID
   • Product_ID: 产品ID
   • Gender: 用户性别
   • Age: 年龄段
   • Occupation: 职业（出于隐私保护，已对数据进行替换处理）
   • City_Category: 城市分类（A、B、C）
   • Stay_In_Current_City_Years: 在当前城市居住的年数
   • Marital_Status: 婚姻状况
   • Product_Category_1: 产品类别（出于隐私保护，已对数据进行替换处理）
   • Product_Category_2: 产品可能属于其他类别（出于隐私保护，已对数据进行替换处理）
   • Product_Category_3: 产品可能属于其他类别（出于隐私保护，已对数据进行替换处理）
   • Purchase: 购买金额（目标变量）

四、项目代码

1. 导入项目所需的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

  这段代码导入了一些常用的数据分析和可视化库，包括NumPy、Pandas、Matplotlib和Seaborn：

  • import numpy as np：导入NumPy库，并将其命名为np。NumPy是用于进行数值计算和数组操作的Python库。
  • import pandas as pd：导入Pandas库，并将其命名为pd。Pandas是一个强大的数据分析库，提供了用于处理和分析数据的数据结构和函数。
  • import matplotlib.pyplot as plt：导入Matplotlib库中的pyplot模块，并将其命名为plt。Matplotlib是一个用于创建静态、动态和交互式可视化的绘图库。
  • import seaborn as sns：导入Seaborn库，并将其命名为sns。Seaborn是一个基于Matplotlib的数据可视化库，提供了更高级别的接口和美观的图形主题。

  通过导入这些库，您可以使用它们提供的函数和工具来进行数据分析、数据可视化以及其他相关任务。

2. 读取数据集

data = pd.read_csv("BlackFridaySales.csv")
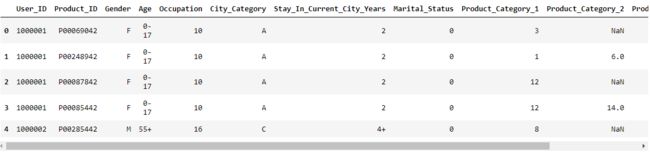
data.head()

• 运行结果如下：

  这段代码加载了一个名为"BlackFridaySales.csv"的CSV文件，并使用Pandas库中的read_csv()函数将其读取为一个数据框（DataFrame）对象，并将该对象存储在名为data的变量中。
  • pd.read_csv("BlackFridaySales.csv")：使用Pandas库的read_csv()函数读取名为"BlackFridaySales.csv"的CSV文件。CSV文件是一种常见的以逗号分隔值的文件格式，用于存储表格数据。read_csv()函数会将CSV文件解析为一个数据框对象，并返回该对象。
  • data.head()：使用head()函数显示data数据框的前几行，默认情况下是前五行。该函数用于快速查看数据框的内容，以确保数据正确加载并了解数据的结构。

  通过这段代码，将数据集文件中的数据加载到名为data的数据框中，并使用data.head()函数查看了数据框的前几行。

查看数据集的形状：

data.shape

• 运行结果如下：

  我们使用 data.shape 来获取数据框 data 的形状信息。运行结果 (550068, 12) 表示数据框 data 包含 550,068 行和 12 列的数据。这意味着原始 CSV 文件中有 550,068 条记录（每一行代表一条记录），并且每条记录包含 12 个不同的属性或特征（每一列代表一个属性）。

查看 data 的详细信息：

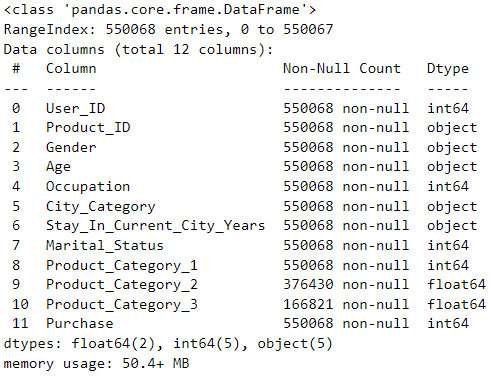
data.info()

• 运行结果如下：

  data.info() 提供了数据框 data 的详细信息摘要。下面是对输出结果的解释：

  • 表明 data 是一个 Pandas 数据框（DataFrame）对象。
  • RangeIndex: 550068 entries, 0 to 550067 表示数据框的索引范围是从 0 到 550067，共有 550068 条记录。
  • Data columns (total 12 columns): 表明数据框共有 12 列。

  接下来的表格显示了每一列的详细信息：

  • Column 列出了列的名称。
  • Non-Null Count 显示了每列的非空值数量，即没有缺失值的记录数。
  • Dtype 显示了每列的数据类型。
  • 最后一行显示了数据框的内存占用情况，表示整个数据框的内存占用为 50.4+ MB。

  根据这些信息，我们可以了解到数据框 data 中的各个列的名称、非空值的数量、数据类型以及整个数据框的内存占用情况。此外，还可以看到有两列（Product_Category_2 和 Product_Category_3）存在缺失值，因为它们的非空值数量少于总记录数。这个信息摘要有助于进一步了解数据的结构、数据类型和缺失值情况，为后续的数据处理和分析提供了基础。

3. 检查缺失值

  检查缺失值的作用是为了了解数据集中是否存在缺失数据，即某些观测值或特征的值是空的或未记录的。缺失值可能对数据分析和建模产生不良影响，因此检查缺失值具有以下重要作用：

  1. 数据完整性：检查缺失值可以帮助确保数据集的完整性。缺失数据可能导致信息不完整，从而影响分析和模型的准确性。
  2. 数据处理：在进行数据处理和分析之前，需要了解数据中的缺失值情况。根据缺失值的分布和类型，可以选择适当的处理方法，如删除包含缺失值的行/列、填充缺失值或使用其他插补技术。
  3. 特征选择：缺失值的存在可能会导致特征的信息缺失或偏差。通过检查缺失值，可以评估每个特征的缺失比例，进而决定是否保留或舍弃某些特征。
  4. 模型建立：许多机器学习算法对缺失值敏感，因此在构建模型之前，需要处理或填充缺失值。检查缺失值有助于决定处理缺失值的方法，以确保模型的准确性和可靠性。

  检查缺失值是数据预处理的关键步骤，它能够帮助我们理解数据的完整性、决策数据处理方法，并确保建立准确和可靠的模型。我们可以通过以下代码检查数据集的缺失值分布情况：

data.isnull().sum()

• 运行结果如下：

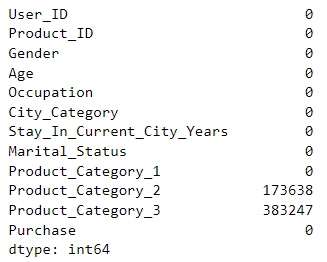
  data.isnull() 返回一个与数据框 data 大小相同的布尔值数据框，其中每个元素表示对应位置是否为空值。接着，.sum() 对布尔值数据框进行求和操作，统计每列的空值数量。
  下面是对输出结果的解释：

  • 每列的名称是输出结果的索引。
  • 每列的数值表示该列中的空值数量。

  根据输出结果，可以得出以下信息：

  • Product_Category_2 列中有 173638 个空值，表示该列有 173638 条记录缺失了数据。
  • Product_Category_3 列中有 383247 个空值，表示该列有 383247 条记录缺失了数据。

  这个结果表明了每列中缺失值的数量。缺失值表示某些记录在相应列中没有提供数据。了解缺失值的分布情况有助于我们在后续的数据处理和分析中选择合适的方法来处理这些缺失值，例如填充、删除或插值等。

★ 探索性数据分析（EDA）：

  探索性数据分析（Exploratory Data Analysis，简称EDA）是一种数据分析方法，旨在通过可视化和统计技术来了解数据集的特征、发现模式、检测异常值，并获取对数据的初步洞察。EDA是数据分析的关键步骤，有助于为后续的建模和推断性分析做好准备。
  以下是探索性数据分析的一些常见任务和目的：

  • 1. 数据摘要：通过计算数据集的描述性统计量（如均值、中位数、标准差等），了解数据的分布、中心趋势和离散程度。
  • 2. 数据可视化：通过绘制图表（如直方图、箱线图、散点图等）来可视化数据的分布、关系和趋势。可视化可以帮助发现数据中的模式、异常值和关联性。
  • 3. 特征相关性：通过计算特征之间的相关系数或绘制相关矩阵热图，了解特征之间的相关性。这有助于确定哪些特征对目标变量有重要影响，以及特征之间是否存在多重共线性。
  • 4. 缺失值和异常值处理：通过检查缺失值和异常值的分布和模式，决定如何处理它们。可以使用插补方法填充缺失值，并选择适当的异常值处理策略。
  • 5. 数据分布和偏度：通过观察数据的分布和偏度情况，了解数据的形态和分布特征。这对于选择适当的建模技术和转换数据（如对数转换或归一化）具有重要意义。
  • 6. 群集和聚类分析：通过应用聚类算法（如K均值聚类、层次聚类等），将数据样本划分为不同的群集，并探索样本之间的相似性和差异性。

  通过EDA，我们能够深入了解数据集，发现数据的特征和规律，并为后续的数据预处理、特征工程和建模过程提供基础。EDA有助于提高数据分析的准确性、可靠性和解释性，同时也有助于生成新的研究假设和发现新的洞察。下面是探索性数据分析的具体实现。

4.可视化目标变量 “Purchase” (购买金额)

sns.distplot(data["Purchase"],color='r')
plt.title("Purchase Distribution")
plt.show()

• 运行结果如下：

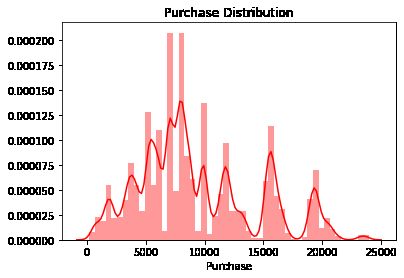
  这段代码使用了Seaborn库和Matplotlib库来绘制名为"Purchase"的列的分布图：

  • sns.distplot(data["Purchase"], color='r')：这行代码使用Seaborn库中的distplot()函数绘制了"Purchase"列的分布图。data["Purchase"]表示从数据框data中选择"Purchase"列的数据作为绘图的输入。color='r'表示设置绘图的颜色为红色。distplot()函数绘制直方图并估计核密度曲线，以显示数据的分布情况。
  • plt.title("Purchase Distribution")：这行代码使用Matplotlib库中的title()函数设置图形的标题为"Purchase Distribution"，用于描述图形的主题或内容。
  • plt.show()：这行代码显示生成的图形。

  通过这段代码，您可以查看"Purchase"列的分布情况，并了解该列中数值的分布范围、峰值和形状。图形的横轴表示"Purchase"的数值，纵轴表示相应数值的频率或概率密度。这样的可视化可以帮助您对"Purchase"数据的整体分布有一个直观的了解。

sns.boxplot(data["Purchase"])
plt.title("Boxplot of Purchase")
plt.show()

• 运行结果如下：

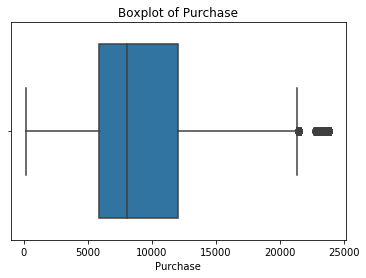
• 运行结果如下：
  这段代码使用了Seaborn库和Matplotlib库来绘制名为"Purchase"的列的箱线图：

  • sns.boxplot(data["Purchase"])：这行代码使用Seaborn库中的boxplot()函数绘制了"Purchase"列的箱线图。data["Purchase"]表示从数据框data中选择"Purchase"列的数据作为绘图的输入。箱线图用于显示数据的分布情况，包括中位数、四分位数、异常值等。
  • plt.title("Boxplot of Purchase")：这行代码使用Matplotlib库中的title()函数设置图形的标题为"Boxplot of Purchase"，用于描述图形的主题或内容。
  • plt.show()：这行代码显示生成的图形。

  通过这段代码，您可以查看"Purchase"列的箱线图，以了解该列中数值的分布情况，包括中位数、四分位数、异常值等。箱线图可以帮助您判断数据的离散程度、异常值的存在以及数据的集中趋势。

下面查看 “Purchase” 的列的偏度：

data["Purchase"].skew()

• 运行结果如下：

  代码data["Purchase"].skew() 是一个函数调用，用于计算数据框 data 中名为 “Purchase” 的列的偏度（skewness）。

  偏度是描述数据分布偏斜程度的统计量，它衡量了数据分布的不对称性。当偏度为正值时，表示数据分布右偏（正偏），即数据的尾部在右侧延伸，也就是数据集中的值偏向较小的一侧；当偏度为负值时，表示数据分布左偏（负偏），即数据的尾部在左侧延伸，数据集中的值偏向较大的一侧；当偏度接近于0时，表示数据分布相对对称。
  通过运行 data["Purchase"].skew()，可以得到 “Purchase” 列的偏度值。这个值可以帮助我们判断数据分布的偏斜程度，从而了解数据的整体特征。
  （请注意，偏度只提供了数据分布的一个方面信息，更全面的数据分布分析还需要结合其他统计量和图形化分析方法来进行。）

  该运行结果表示 “Purchase” 列的偏度为 0.6001400037087128。根据输出结果，我们可以得出结论：
  • “Purchase” 列的偏度为正值（0.6001400037087128），说明该列的数据分布略微呈现右偏形态。
  • 右偏表明数据的尾部在右侧延伸，也就是数据集中的值偏向较小的一侧。

  这个结果表明在 “Purchase” 列中，较小的购买金额的值较为集中，而较大的购买金额的值相对较少。然而，由于偏度值并不是非常大，因此数据分布的右偏程度并不明显。

下面查看 “Purchase” 的列的峰度：

data["Purchase"].kurtosis()

• 运行结果如下：

  代码data["Purchase"].kurtosis() 是一个函数调用，用于计算数据框 data 中名为 “Purchase” 的列的峰度（kurtosis）。

  峰度是描述数据分布峰态的统计量，它衡量了数据分布的尖锐程度或厚尾程度。正常分布的峰度为3，如果数据的峰度大于3，则表示数据分布比正态分布更尖锐（尖峰），而如果数据的峰度小于3，则表示数据分布比正态分布更平缓（厚尾）。
  通过运行 data["Purchase"].kurtosis()，可以得到 “Purchase” 列的峰度值。这个值可以帮助我们判断数据分布的尖锐程度或厚尾程度，从而了解数据的整体特征。
  （请注意，峰度只提供了数据分布的一个方面信息，更全面的数据分布分析还需要结合其他统计量和图形化分析方法来进行。）

  该运行结果表示 “Purchase” 列的峰度为 -0.3383775655851702。根据峰度的定义，正峰度值大于3表示数据分布尖峰，而负峰度值小于3表示数据分布厚尾。因此，根据输出结果，我们可以得出结论：

  • “Purchase” 列的峰度为负值 -0.3383775655851702，表示数据分布相对于正态分布来说略微厚尾。

  这个结果表明 “Purchase” 列的数据分布相对平缓，尾部相对较厚，不如正态分布的尾部那么尖锐。峰度值接近于0，说明数据相对于正态分布来说并没有明显的尖峰或厚尾特征。

下面查看 “Purchase” 的列的基本统计描述信息：

data["Purchase"].describe()

• 运行结果如下：

  代码data["Purchase"].describe() 是一个函数调用，用于计算数据框 data 中名为 “Purchase” 的列的基本统计描述信息。该函数会计算 “Purchase” 列的以下统计量：

  • count：非空值的数量。
  • mean：平均值。
  • std：标准差。
  • min：最小值。
  • 25%：第一四分位数。
  • 50%：中位数（第二四分位数）。
  • 75%：第三四分位数。
  • max：最大值。

  过运行 data["Purchase"].describe()，我们可以得到关于 “Purchase” 列的重要统计信息：

  • “Purchase” 列共有 550,068 个非空值。
  • 平均购买金额为 9,263.97。
  • 购买金额的标准差为 5,023.07，说明购买金额的变动较大。
  • 购买金额的最小值为 12，最大值为 23,961。
  • 25% 的数据小于或等于 5,823，50% 的数据小于或等于 8,047，75% 的数据小于或等于 12,054。

  这些统计量提供了关于数据分布、中心位置、离散程度以及数据的最大和最小值的信息。它们有助于描述和总结 “Purchase” 列的数据特征，帮助我们了解数据的整体情况。

5. 统计"Gender"（性别）列

可视化男女性别的频数分布情况：

sns.countplot(data['Gender'])
plt.show()

• 运行结果如下：

  这段代码使用了 seaborn（sns）和 matplotlib 库来创建一个针对数据框 data 中 “Gender” 列的计数柱状图，并显示图形。具体解释如下：

  • sns.countplot(data['Gender'])：这行代码使用 seaborn 库的 countplot() 函数来创建一个计数柱状图。data['Gender'] 表示选择数据框 data 中的 “Gender” 列作为绘图的数据。countplot() 函数将根据 “Gender” 列的不同取值进行计数，并将结果可视化为柱状图。
  • plt.show()：这行代码使用 matplotlib 库的 show() 函数来显示图形。在创建完图形后，调用 show() 函数将图形显示出来。

  通过这个图形，可以直观地了解 “Gender” 列的数据分布和类别计数情况。

下面查看男女性别的占比分布：

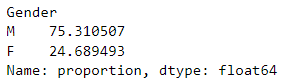
data['Gender'].value_counts(normalize=True)*100

• 运行结果如下：

  通过运行 data['Gender'].value_counts(normalize=True)*100，我们得到了 “Gender”（性别） 列每个类别的频率百分比。结果表明，在数据集中，男性的比例为 75.31%，女性的比例为 24.69%。这些百分比可以帮助我们了解样本中不同性别的分布情况，并进行进一步的分析。

查看不同性别的购买金额平均水平：

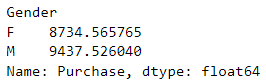
grouped_data = data.groupby("Gender")["Purchase"].mean()
grouped_data

• 运行结果如下：

  这段代码使用 groupby() 方法对数据框 data 按照 “Gender” 列进行分组，并计算每个分组中 “Purchase” 列的平均值。具体解释如下：

  • data.groupby("Gender")：这部分代码使用 groupby() 方法将数据框 data 按照 “Gender” 列的唯一值进行分组。这将创建一个分组对象，其中包含了按照 “Gender” 列分组后的数据。
  • ["Purchase"]：这部分代码指定了我们想要获取的列，即 “Purchase” 列。只选择 “Purchase” 列作为计算平均值的列。
  • .mean()：这部分代码调用 mean() 方法，对分组后的 “Purchase” 列进行求平均操作。对于每个分组，计算 “Purchase” 列的平均值。

  通过运行 grouped_data = data.groupby("Gender")["Purchase"].mean()，我们得到了按照 “Gender” 列分组后，每个组中 “Purchase” 列的平均值。将结果存储在名为 grouped_data 的变量中。结果表明，女性的平均购买金额为 8734.565765，男性的平均购买金额为 9437.526040。这些结果可以帮助我们了解不同性别之间的购买行为差异，以及在营销和市场策略中进行性别定向的决策依据。

6. 统计"Marital Status"（婚姻状况）列

可视化婚姻状况的频数分布情况：

sns.countplot(data['Marital_Status'])
plt.show()

• 运行结果如下：

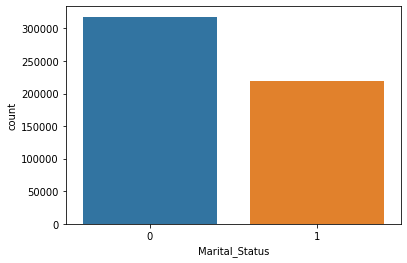
  该段代码创建一个计数柱状图，用于可视化数据框 data 中 “Marital_Status” 列的不同取值的频数。通过这个图形，可以直观地了解 “Marital_Status” 列的数据分布和类别计数情况。通过直方图可以发现，在该数据集中，未婚的比已婚的人数更多。

查看不同婚姻状况的购买金额平均水平：

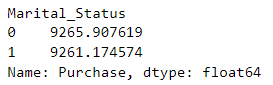
grouped_data = data.groupby("Marital_Status")["Purchase"].mean()
grouped_data

• 运行结果如下：

  这段代码使用 groupby() 方法对数据框 data 按照 “Marital_Status” 列进行分组，并计算每个分组中 “Purchase” 列的平均值。结果表明，未婚者的平均购买金额为 9265.907619，已婚者的平均购买金额为 9261.174574。这些结果可以帮助我们了解不同婚姻状况之间的购买行为差异，以及在营销和市场策略中进行婚姻状况定向的决策依据。

可视化按照 “Marital_Status” 列分组后的购买金额平均值:

grouped_data.plot(kind='bar')
plt.title("Marital_Status and Purchase Analysis")
plt.show()

• 运行结果如下：

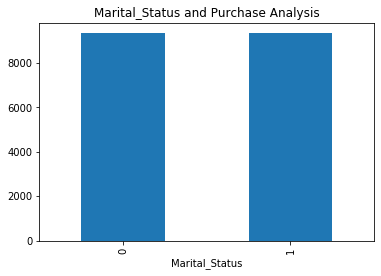
  我们可以发现，尽管未婚人士在购买上花费更多，但已婚和未婚人士的平均购买金额是相同的。

7. 统计"Occupation"（职业）列

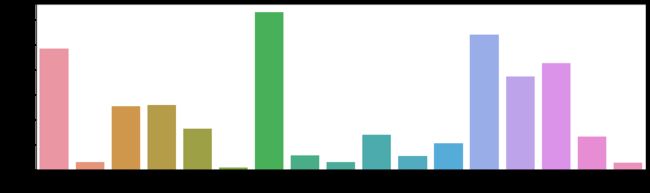
可视化职业的频数分布：

plt.figure(figsize=(18,5))
sns.countplot(data['Occupation'])
plt.show()

• 运行结果如下：

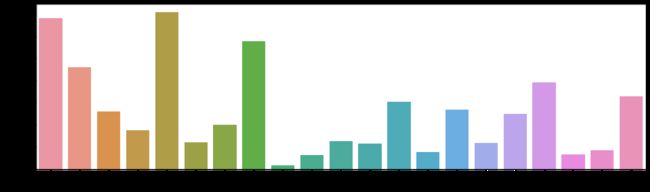
  * 注：由于隐私保护，原数据集已将职业用数字替换，每一个数字代表一类职业。
  该段代码使用 seaborn 库的 countplot() 函数绘制了一个计数条形图，显示了不同职业的计数情况。通过这个图形，可以直观地了解每个职业的频数分布。

统计不同职业组的平均购买金额：

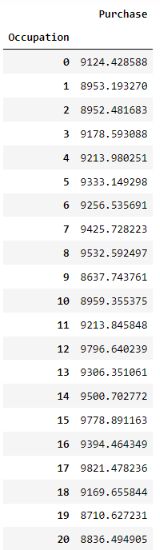
occup = pd.DataFrame(data.groupby("Occupation")["Purchase"].mean())
occup

运行结果如下：

  这段代码根据 “Occupation” 列对数据进行分组，并计算每个职业组中 “Purchase” 列的平均值。结果被存储在一个名为 occup 的新数据框中。该数据可以用于进一步分析和可视化不同职业组的购买金额平均水平，帮助了解不同职业之间的购买行为差异。

可视化不同职业组的购买金额平均值：

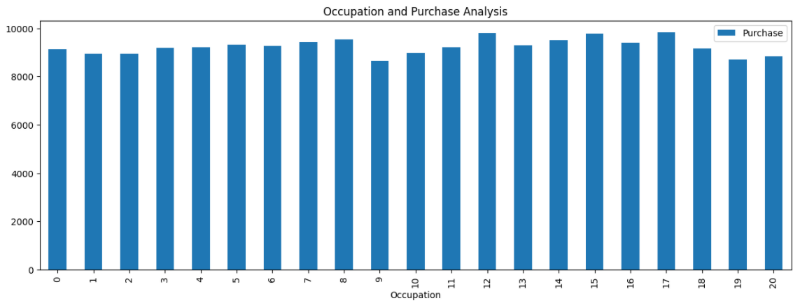
occup.plot(kind='bar',figsize=(15,5))
plt.title("Occupation and Purchase Analysis")
plt.show()

• 运行结果如下：

  该段代码根据按照职业分组后的购买金额平均值，创建一个条形图来可视化不同职业组的购买金额平均值。通过这个图形，可以直观地比较不同职业之间的购买金额差异。由统计直方图可以看出，尽管某些职业的的购买金额平均值更高，但每个用户的平均消费金额在各个职业间大致相同。

8. 统计"City_Category"（城市类别）列

可视化不同城市类别的频数分布：

sns.countplot(data['City_Category'])
plt.show()

• 运行结果如下：

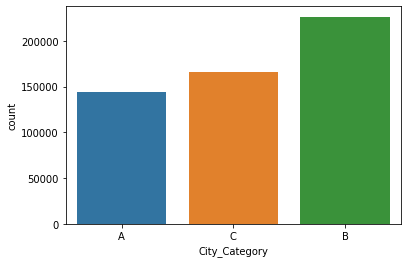
  这段代码使用 seaborn 库绘制了一个计数条形图，用于可视化 “City_Category” 列的计数情况。具体解释如下：

  • sns.countplot(data['City_Category'])：这行代码使用 seaborn 库的 countplot() 函数绘制了一个计数条形图，显示了 “City_Category” 列中每个城市类别的计数。data['City_Category'] 表示从数据框中选择 “City_Category” 列作为绘图的数据。
  • plt.show()：这行代码使用 matplotlib 库的 show() 函数显示图形。

  通过条形图，可以发现B类城市频数分布最多，A类城市分布最少。

可视化按照城市类别分组后的购买金额平均值：

data.groupby("City_Category")["Purchase"].mean().plot(kind='bar')
plt.title("City Category and Purchase Analysis")
plt.show()

• 运行结果如下：

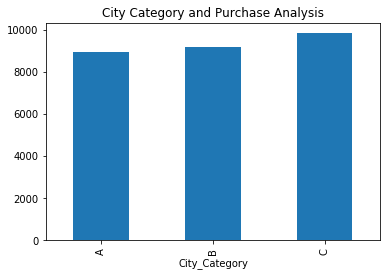
  该段代码根据按照城市类别分组后的购买金额平均值，创建一个条形图来可视化不同城市类别的购买金额平均值。通过这个图形，可以直观地比较不同城市类别之间的购买金额差异。我们可以发现，C类城市的平均消费金额最多。

9. 统计"Stay_In_Current_City_Years"（在当前城市居住的年数）列

可视化不同城市类别的频数分布：

sns.countplot(data['Stay_In_Current_City_Years'])
plt.show()

• 运行结果如下：

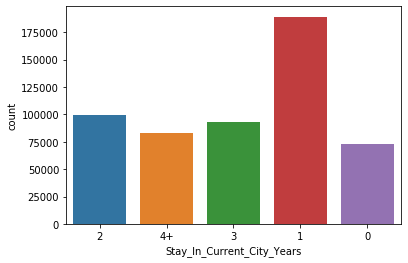
  根据条形图可以发现一个人在某个城市居住的时间越长，购买新物品的倾向就越低。因此，如果有人刚搬到一个新城市，并且需要很多新东西来装饰他们的房子，他们会利用黑色星期五的低价购买所有所需物品。

可视化按照停留年限分组后的购买金额平均值：

data.groupby("Stay_In_Current_City_Years")["Purchase"].mean().plot(kind='bar')
plt.title("Stay_In_Current_City_Years and Purchase Analysis")
plt.show()

• 运行结果如下：

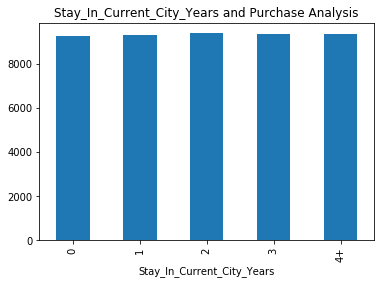
  根据统计图可以发现，刚来到城市的人负责更多的购买次数，然而，从个体来看，他们在无论在当前城市居住了多少年的情况下，花费的金额倾向是相同的。

10. 统计"Age"（年龄）列

可视化年龄的频数分布情况：

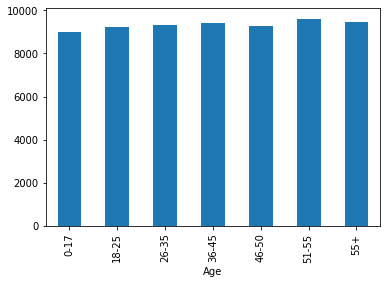
sns.countplot(data['Age'])
plt.title('Distribution of Age')
plt.xlabel('Different Categories of Age')
plt.show()

• 运行结果如下：

  该段代码的作用是创建一个计数条形图，通过 seaborn 库的 countplot() 函数可视化了不同年龄段的计数情况。通过这个图形，可以直观地了解每个年龄段的频数分布。根据结果可以发现，年龄组为26-35岁的人群中，购买次数最多。

可视化按照年龄段分组后的购买金额平均值：

data.groupby("Age")["Purchase"].mean().plot(kind='bar')

• 运行结果如下：

  该段代码根据按照年龄段分组后的购买金额平均值，创建一个条形图来可视化不同年龄段的购买金额平均值。通过这个图形，可以直观地比较不同年龄段之间的购买金额差异。我们可以发现在不同年龄组之间，平均购买率倾向于相同，只有51-55岁的年龄组的平均购买金额稍高一些。

可视化按照年龄段分组后的购买金额总和：

data.groupby("Age")['Purchase'].sum().plot(kind="bar")
plt.title("Age and Purchase Analysis")
plt.show()

• 运行结果如下：

  该段代码根据按照年龄段分组后的购买金额总和，创建一个条形图来可视化不同年龄段的购买金额总和。通过这个图形，可以直观地比较不同年龄段之间的购买金额差异。我们可以发现，购买总金额与购买次数按年龄分布是一致的。

11. 统计"Product_Category_1"（产品类别1）列

可视化不同产品类别的频数分布情况：

plt.figure(figsize=(18,5))
sns.countplot(data['Product_Category_1'])
plt.show()

• 运行结果如下：

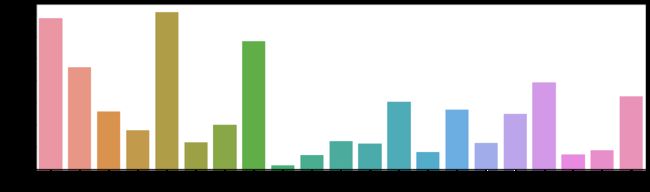
可视化按照 “Product_Category_1” 列分组后的购买金额平均值：

data.groupby('Product_Category_1')['Purchase'].mean().plot(kind='bar',figsize=(18,5))
plt.title("Product_Category_1 and Purchase Mean Analysis")
plt.show()

• 运行结果如下：

  该段代码根据按照产品类别分组后的购买金额平均值，创建一个条形图来可视化不同产品类别的购买金额平均值。通过这个图形，可以直观地比较不同产品类别之间的购买金额差异。根据运行结果你会发现尽管1、5、8类别的产品购买数量更多，但这三个类别的平均消费金额并不是最高的。有趣的是，尽管对销售数量影响较小，但其他类别出现了高额购买金额。

可视化按照 “Product_Category_1” 列分组后的购买金额总和：

data.groupby('Product_Category_1')['Purchase'].sum().plot(kind='bar',figsize=(18,5))
plt.title("Product_Category_1 and Purchase Analysis")
plt.show()

• 运行结果如下：

  该段代码根据按照产品类别分组后的购买金额总和，创建一个条形图来可视化不同产品类别的购买金额总和。通过这个图形，可以直观地比较不同产品类别之间的购买金额差异。

12. 统计"Product_Category_2"（产品类别2）列

可视化不同产品类别的频数分布情况：

plt.figure(figsize=(18,5))
sns.countplot(data['Product_Category_2'])
plt.show()

• 运行结果如下：

13. 统计"Product_Category_3"（产品类别3）列

可视化不同产品类别的频数分布情况：

plt.figure(figsize=(18,5))
sns.countplot(data['Product_Category_3'])
plt.show()

• 运行结果如下：

14. 绘制列之间的相关性热力图

计算数值列之间的相关性：

string_columns = data.select_dtypes(include=['object']).columns
data1 = data.drop(string_columns, axis=1)
data1.corr()

• 运行结果如下：

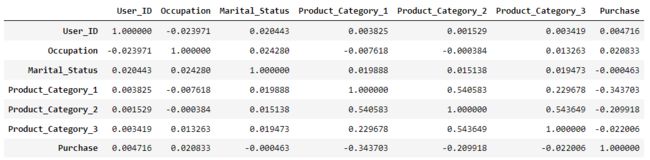
  这段代码的作用是计算数据框 data 中数值列之间的相关性。具体解释如下：

  • string_columns = data.select_dtypes(include=['object']).columns：这行代码使用 select_dtypes() 方法选择数据框中数据类型为 “object”（字符串）的列，并将这些列的列名存储在 string_columns 变量中。
  • data1 = data.drop(string_columns, axis=1)：这行代码使用 drop() 方法删除数据框 data 中的 string_columns 列，即将数据框中的字符串列移除，并将结果存储在 data1 变量中。
  • data1.corr()：这部分代码调用 corr() 方法计算 data1 数据框中数值列之间的相关性。结果是一个相关性矩阵，其中每个单元格表示对应两个列之间的相关性系数。

  综合起来，该段代码的作用是将数据框 data 中的字符串列移除，然后计算数值列之间的相关性，得到一个相关性矩阵。这可以帮助我们了解数值列之间的线性相关程度，有助于发现变量之间的关联性。

然后，绘制列之间的相关性热力图：

sns.heatmap(data1.corr(),annot=True)
plt.show()

• 运行结果如下：

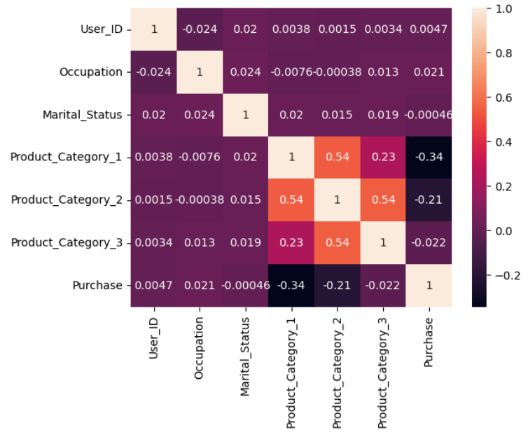
  运行这段代码后，生成了一个热力图，其中展示了相关性矩阵 data1.corr() 中各个变量之间的相关性。在热力图中，每个单元格的颜色表示对应两个变量之间的相关性强度，颜色越深表示相关性越强，颜色越浅表示相关性越弱。此外，参数 annot=True 用于在热力图中显示相关性系数的数值。
  通过观察热力图，可以更直观地了解不同变量之间的相关性模式。强正相关的变量在热力图中呈现深色方块，而强负相关的变量则呈现浅色方块。无相关性或较弱的相关性会在热力图中表现为中间色调或浅色。通过该可视化可以帮助我们发现变量之间的相关性模式，并为进一步的数据分析和建模提供有价值的洞察。
  通过热力图我们可以发现，产品类别组之间存在一定的相关性。

★ 数据处理：

  数据处理是指对原始数据进行清洗、转换和整理的过程，以便进行进一步的分析和应用。在数据处理过程中，通常会包括以下几个主要步骤：

1. 数据清洗：识别和处理数据中的错误、缺失、异常或重复值。这包括去除无效或不完整的数据记录，填补缺失值，修复错误数据等。

2. 数据转换：对数据进行转换，以满足分析或应用的需求。这可能包括对数据进行标准化、归一化、离散化、聚合等操作，以便于后续的统计分析或机器学习算法的应用。

3. 特征选择：根据分析目标和问题的需要，选择最相关的特征或变量，而舍弃或删除不相关或冗余的特征。这有助于减少数据维度，提高模型的效率和解释性。

4. 数据集成：将来自不同数据源或不同格式的数据进行合并和整合，以创建一个统一的数据集。这可以通过连接、合并、拼接等操作来完成。

5. 数据规约：对大型数据集进行抽样、压缩或聚合，以减少数据量和存储需求，同时保持对整体数据集的代表性。

6. 数据处理的可视化：使用图表、图形或可视化工具，对处理后的数据进行展示和探索，以便更好地理解数据的分布、关系和趋势。

  通过这些数据处理步骤，可以清理和准备好的数据将更有利于后续的分析、建模和决策制定。数据处理的目标是提高数据的质量和可用性，使得数据能够为业务和研究带来更有价值的洞察和见解。

15. 对分类变量进行编码

创建副本：

df = data.copy()

对 df 进行独热编码：

df = pd.get_dummies(df, columns=['Stay_In_Current_City_Years'])

  这两段代码先使用copy()方法创建了一个data数据帧的副本，并将其赋值给新的数据帧df，( 创建副本的目的是为了在进行数据处理和分析时保留原始数据的完整性,通过对副本进行操作，可以避免对原始数据帧产生不可逆的更改，以便在需要时可以回到原始数据的状态。) 然后对数据帧df中的Stay_In_Current_City_Years列进行独热编码处理，并将编码后的结果添加到df中。解释代码的作用：

• pd.get_dummies(df, columns=['Stay_In_Current_City_Years']): 这行代码使用Pandas库的get_dummies()函数对df数据帧中的Stay_In_Current_City_Years列进行独热编码处理。columns=['Stay_In_Current_City_Years']指定了要进行独热编码处理的列名。

  独热编码是一种将分类变量转换为二进制向量的方法。对于Stay_In_Current_City_Years列，如果有n个不同的取值，独热编码将创建n个新的二进制列，每个列表示原始列中的一个取值。对于每一行，只有对应取值的列为1，其他列为0。这样可以将分类变量转换为机器学习算法更易于处理的形式。
  通过对df进行独热编码处理，可以将Stay_In_Current_City_Years列转换为多个二进制列，并将编码后的结果添加到df数据帧中。这样可以在进一步的数据分析和建模过程中使用这些编码后的列。

from sklearn.preprocessing import LabelEncoder
lr = LabelEncoder()

  这段代码导入了sklearn.preprocessing模块中的LabelEncoder类，并创建了一个名为lr的LabelEncoder对象。下面解释代码的作用：

• from sklearn.preprocessing import LabelEncoder: 这行代码从sklearn.preprocessing模块中导入LabelEncoder类。LabelEncoder用于将分类变量转换为数值标签，使得机器学习算法能够处理这些标签。
• lr = LabelEncoder(): 这行代码创建了一个名为lr的LabelEncoder对象。lr对象是LabelEncoder类的实例，可以用于对分类变量进行标签编码。

  通过导入LabelEncoder类并创建lr对象，您可以使用lr对象对分类变量进行标签编码，将其转换为数值标签。这样可以在机器学习算法中使用这些编码后的数值来进行训练和预测。

df['Gender'] = lr.fit_transform(df['Gender'])

  这段代码使用先前创建的lr对象，对数据帧df中的Gender列进行标签编码，并将编码后的结果覆盖到原始的Gender列中。下面解释代码的作用：

• df['Gender']: 这部分代码指定了要操作的列为df数据帧中的Gender列。
• lr.fit_transform(df['Gender']): 这部分代码使用之前创建的lr对象，对Gender列进行标签编码转换。fit_transform()方法首先对Gender列进行拟合（学习标签编码的映射关系），然后对该列进行转换得到编码后的结果。
• df['Gender'] = lr.fit_transform(df['Gender']): 这部分代码将编码后的结果覆盖到原始的Gender列中，实现了对Gender列的标签编码操作。

  标签编码将分类变量转换为整数标签，其中每个不同的类别将映射到一个唯一的整数值。通过将分类变量转换为数值标签，可以在机器学习算法中更好地处理这些特征，并帮助算法理解类别之间的相对关系。

df['Age'] = lr.fit_transform(df['Age'])

  这段代码使用先前创建的lr对象，对数据帧df中的Age列进行标签编码，并将编码后的结果覆盖到原始的Age列中。

df['City_Category'] = lr.fit_transform(df['City_Category'])

  这段代码使用先前创建的lr对象，对数据帧df中的City_Category列进行标签编码，并将编码后的结果覆盖到原始的City_Category列中。

查看编码后的数据帧前五行：

df.head()

• 运行结果如下：

  可以看到进行了标签编码之后，Gender、Age和City_Category列现在的数据变成了整数值，而不是之前的分类变量。

16. 缺失值替换

df['Product_Category_2'] =df['Product_Category_2'].fillna(0).astype('int64')
df['Product_Category_3'] =df['Product_Category_3'].fillna(0).astype('int64')

  这段代码对数据帧df中的Product_Category_2列和Product_Category_3列进行缺失值处理，并将缺失值替换为0，并将列的数据类型转换为整数类型（int64），以便于数据更适合进行后续的分析和建模。

下面查看数据帧 df 每列的缺失值情况：

df.isnull().sum()

• 运行结果如下：

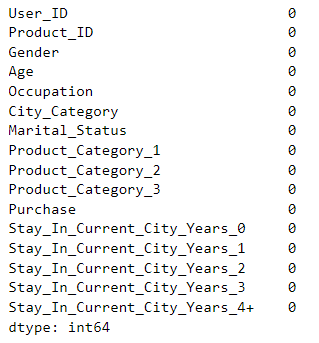
  可以看到，现在数据帧已没有缺失值，下面可以对数据进行进一步的分析和处理。

17. 删除不相关的列

df = df.drop(["User_ID","Product_ID"],axis=1)

  这段代码从数据帧df中删除了名为User_ID和Product_ID的两列，这是因为它们在分析或建模过程中不被使用，删除它们可以减少数据集的维度，简化分析过程，提高分析效率和速度。

18. 划分训练集和测试集

X = df.drop("Purchase",axis=1)
y = df['Purchase']

  这段代码将数据帧df中的Purchase列作为目标变量，并将其从df中删除，然后将剩余的列作为特征矩阵赋值给变量X，将Purchase列赋值给变量y。通过这段代码将数据帧df被拆分成了特征矩阵X和目标变量y。X包含了除了Purchase列以外的所有特征列，用于训练模型。y包含了Purchase列的值，用作模型的目标进行训练和预测。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=123)

  这段代码使用train_test_split函数从特征矩阵X和目标变量y中划分出训练集和测试集。下面解释代码的作用：

• train_test_split(X, y, test_size=0.3, random_state=123): 这部分代码调用train_test_split函数进行数据集划分。参数X表示特征矩阵，y表示目标变量。test_size=0.3表示测试集的比例为30%，训练集的比例为70%。random_state=123是一个随机种子，用于控制随机划分的过程，保证每次运行代码时得到的划分结果相同。
• X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=123): 这部分代码将train_test_split函数返回的划分结果分别赋值给变量X_train、X_test、y_train和y_test。其中，X_train和y_train表示训练集的特征矩阵和目标变量，X_test和y_test表示测试集的特征矩阵和目标变量。

  通过这段代码，特征矩阵X和目标变量y被划分为训练集和测试集。训练集用于训练机器学习模型，测试集用于评估模型的性能和泛化能力。划分过程使用了30%的数据作为测试集，并使用随机种子保证了划分结果的可复现性。

★ 构建模型：

19. 构建线性回归模型

  线性回归是一种用于建模和预测连续数值变量的统计分析方法。它基于线性关系假设，通过拟合一个直线或超平面来描述自变量（输入特征）与因变量（输出目标）之间的关系。
  线性回归模型的基本形式可以表示为：Y = β0 + β1X1 + β2X2 + … + βnXn + ε
  其中，Y表示因变量（要预测的目标变量），X1、X2、…、Xn表示自变量（输入特征），β0、β1、β2、…、βn表示模型的参数（斜率），ε表示误差项（随机噪声）。模型的目标是通过调整参数的取值，使得预测值与真实值之间的差距最小化。
  线性回归模型可以通过最小二乘法来估计参数的取值。最小二乘法的目标是最小化残差平方和，即使得预测值与真实值之间的平方差异最小化。
  线性回归模型的优点包括简单易于理解和实现，计算效率高，适用于大规模数据集。然而，线性回归也有一些限制，例如它假设自变量和因变量之间的关系是线性的，忽略了非线性关系；还有可能存在多重共线性、异方差性等问题，需要进行适当的处理和检验。
  在实际应用中，线性回归模型可以用于预测房价、销售量、股票价格等连续数值变量的问题。

首先导入scikit-learn库的线性回归模型：

from sklearn.linear_model import LinearRegression

  这段代码导入了LinearRegression线性回归模型类，该类是scikit-learn库中的一个模型类。通过这段代码，您可以在代码中使用LinearRegression类来构建线性回归模型。

对模型进行训练：

lr = LinearRegression()
lr.fit(X_train,y_train)

  这段代码创建了一个LinearRegression线性回归模型的实例，并使用训练集数据对模型进行训练。下面解释代码的作用：

• lr = LinearRegression(): 这部分代码创建了一个LinearRegression的实例，将其赋值给变量lr。这个实例化的对象将用于构建线性回归模型。
• lr.fit(X_train, y_train): 这部分代码使用训练集数据X_train和y_train对线性回归模型进行训练。fit()方法将根据训练数据拟合模型，学习特征和目标之间的线性关系。

  通过这段代码，线性回归模型lr被实例化，并使用训练集数据进行训练。模型通过学习训练数据中的特征和目标之间的线性关系，尝试找到最佳的回归函数，以便对测试集数据进行预测。

查看线性回归模型中的截距值：

lr.intercept_

• 运行结果如下：

  lr.intercept_ 是线性回归模型中的一个属性，用于获取模型的截距值（intercept）。截距值表示当所有特征的取值都为0时，目标变量的预测值。
  在这个例子中，输出结果 9536.400764131557 表示线性回归模型的截距项的数值为 9536.400764131557。这意味着当所有特征的取值都为0时，模型预测的目标变量（在此处为"Purchase"）的平均值或基准值为 9536.400764131557。
  截距值在线性回归中很重要，它对模型的预测结果起到偏移的作用。当特征的取值不全为0时，截距值会对预测结果进行调整。通过获取截距值，我们可以了解模型在特征为0的情况下的基准预测值。

查看线性回归模型的系数：

lr.coef_

• 运行结果如下：

运行代码 lr.coef_ 的输出结果是一个数组：

array([ 465.82318446,  112.36643445,    5.05508596,  314.06766138,
        -58.23217776, -348.4514785 ,   12.98415047,  143.49190467,
        -20.83796687,    5.4676518 ,   17.68367185,   -3.96751734,
          1.65416056])

  lr.coef_ 是线性回归模型中的一个属性，用于获取模型的系数（coefficients）。这些系数对应于模型中各个特征的权重，表示特征对目标变量的影响程度。
  在这个例子中，输出结果表示线性回归模型中每个特征的系数值，系数的顺序与特征在训练过程中的顺序相对应。根据输出的数组元素顺序，可以对应如下特征：

  • 第一个系数（465.82318446）对应着 Gender 特征。
  • 第二个系数（112.36643445）对应着 Age 特征。
  • 第三个系数（5.05508596）对应着 Occupation 特征。
  • 第四个系数（314.06766138）对应着 City_Category 特征。
  • 第五个系数（-58.23217776）对应着 Marital_Status 特征。
  • 第六个系数（-348.4514785）对应着 Product_Category_1 特征。
  • 第七个系数（12.98415047）对应着 Product_Category_2 特征。
  • 第八个系数（143.49190467）对应着 Product_Category_3 特征。
  • 第九个系数（-20.83796687）对应着 Stay_In_Current_City_Years_0 特征。
  • 第十个系数（5.4676518）对应着 Stay_In_Current_City_Years_1 特征。
  • 第十一个系数（17.68367185）对应着 Stay_In_Current_City_Years_2 特征。
  • 第十二个系数（-3.96751734）对应着 Stay_In_Current_City_Years_3 特征。
  • 第十三个系数（1.65416056）对应着 Stay_In_Current_City_Years_4+ 特征。

  这些系数值表示了每个特征对目标变量（在此处为"Purchase"）的影响程度。正系数表示正相关关系，即特征增加时目标变量也会增加，而负系数表示负相关关系，即特征增加时目标变量会减少。系数的绝对值越大，表示特征对目标变量的影响越大。通过查看 lr.coef_ 的值，可以了解线性回归模型中每个特征的权重，从而理解模型对特征的建模结果。

对测试集进行预测：

y_pred = lr.predict(X_test)

  下面解释代码的作用：

• lr.predict(X_test): 这部分代码调用线性回归模型 lr 的 predict() 方法，传入测试集数据 X_test 作为参数。该方法根据已训练的模型对测试集数据进行预测，并返回预测结果。
• y_pred = lr.predict(X_test): 这部分代码将预测结果存储在变量 y_pred 中。y_pred 是一个数组，其中包含了对测试集数据的预测值。

  通过这段代码，我们使用训练好的线性回归模型 lr 对测试集数据进行预测，得到预测结果存储在变量 y_pred 中。这样，我们就可以与实际的目标变量 y_test 进行比较，评估模型的预测性能。

from sklearn.metrics import mean_absolute_error,mean_squared_error, r2_score

  这段代码导入了三个评估回归模型性能的指标：
  • mean_absolute_error：平均绝对误差（MAE），用于评估预测值与真实值之间的平均绝对差异。
  • mean_squared_error：均方误差（MSE），用于评估预测值与真实值之间的平均平方差异。
  • r2_score：确定系数（R^2），用于评估模型对目标变量方差的解释程度。

  这些指标可以用来评估线性回归模型的性能和预测准确度。

计算平均绝对误差（MAE）：

mean_absolute_error(y_test, y_pred)

• 运行结果如下：

  mean_absolute_error(y_test, y_pred) 的作用是计算预测值 y_pred 和真实值 y_test 之间的平均绝对误差（Mean Absolute Error, MAE）。它衡量了预测值与真实值之间的平均绝对差异，用于评估模型的预测准确度。
  输出结果 3532.0692261658432 是预测值 y_pred 和真实值 y_test 之间的平均绝对误差。该值表示预测值与真实值之间的平均差异程度。通常较小的 MAE 值表示模型的预测能力较好，因为它表示模型的预测值与真实值的平均绝对差异较小。

计算均方误差（MSE）：

mean_squared_error(y_test, y_pred)

• 运行结果如下：

  mean_squared_error(y_test, y_pred) 的作用是计算预测值 y_pred 和真实值 y_test 之间的均方误差（Mean Squared Error, MSE）。它衡量了预测值与真实值之间的平均平方差异，用于评估模型的预测准确度。
  输出结果 21397853.26940752 是预测值 y_pred 和真实值 y_test 之间的均方误差。该值表示预测值与真实值之间的平均平方差异程度。通常较小的 MSE 值表示模型的预测能力较好，因为它表示模型的预测值与真实值的平均平方差异较小。

计算确定系数（$R^2$）：

r2_score(y_test, y_pred)

• 运行结果如下：

  r2_score(y_test, y_pred) 的作用是计算预测值 y_pred 和真实值 y_test 之间的确定系数（R^2 score）。确定系数衡量了模型对目标变量方差的解释程度，用于评估模型的拟合优度。
  输出结果 0.15192944521481666 是预测值 y_pred 和真实值 y_test 之间的确定系数。确定系数的取值范围在 0 到 1 之间，越接近 1 表示模型对目标变量的解释能力越好。在这种情况下，输出结果约为 0.15，意味着模型对目标变量的解释能力较低，只能解释目标变量方差的约15%。

计算均方根误差（RMSE）：

from math import sqrt
print("RMSE of Linear Regression Model is ",sqrt(mean_squared_error(y_test, y_pred)))

• 运行结果如下：

  首先，from math import sqrt 导入了 math 模块中的 sqrt 函数，该函数用于计算给定数字的平方根。
  然后，print("RMSE of Linear Regression Model is ", sqrt(mean_squared_error(y_test, y_pred))) 将打印输出一个字符串和计算得到的 RMSE 值。
  输出结果 "RMSE of Linear Regression Model is 4625.781368526567" 表示线性回归模型的均方根误差为约 4625.78。RMSE 是均方误差的平方根，用于衡量模型的预测误差。较小的 RMSE 值表示模型的预测能力较好，因为它表示模型的预测值与真实值之间的平均差异较小。

20. 构建决策树回归器（DecisionTreeRegressor）模型

  决策树回归器（Decision Tree Regressor）是一种用于回归问题的决策树算法。与分类问题中的决策树类似，决策树回归器使用树状结构来建立预测模型，但其目标是预测连续数值的目标变量。
  决策树回归器的构建过程如下：

1. 数据准备：准备包含输入特征和目标变量的训练数据集。
2. 特征选择：根据一定的指标（例如平方误差或方差减少），选择最佳的特征作为当前节点的分裂依据。
3. 分裂节点：根据选定的特征和分裂依据，将当前节点分裂为多个子节点。
4. 递归建树：对于每个子节点，重复步骤2和步骤3，直到满足停止条件，如达到最大深度或节点样本数量低于阈值。
5. 叶节点预测：在叶节点上，使用目标变量的均值或其他统计量作为预测结果。
6. 预测：对于新的输入样本，根据构建好的决策树回归器，沿着树的路径进行判断，最终到达叶节点并获得预测结果。

  决策树回归器的优点包括易于理解和解释，能够处理非线性关系和离群值，对于缺失值有一定的容忍度。然而，它也容易过拟合训练数据，特别是在树的深度较大时。为了缓解过拟合，可以使用剪枝技术或集成学习方法，如随机森林。
  决策树回归器在许多领域有广泛应用，如房价预测、股票价格预测、销售量预测等。它可以帮助我们理解和分析输入特征对于目标变量的影响，并进行预测和决策。

导入 scikit-learn 库中的 DecisionTreeRegressor 类：

from sklearn.tree import DecisionTreeRegressor

创建决策树回归模型的对象：

regressor = DecisionTreeRegressor(random_state = 0)  

  代码 regressor = DecisionTreeRegressor(random_state = 0) 创建了一个 DecisionTreeRegressor 类的对象 regressor。在创建对象时，使用了 random_state = 0 参数，用于设置随机种子，以确保每次运行模型时得到相同的结果。
  在创建了 regressor 对象后，您可以使用该对象调用相关的方法和属性，例如 fit() 方法用于训练模型，predict() 方法用于进行预测等。

训练模型：

regressor.fit(X_train, y_train)

  regressor.fit(X_train, y_train) 调用了决策树回归模型对象 regressor 的 fit() 方法，将训练数据集 X_train 和对应的目标变量 y_train 作为参数传递给 fit() 方法。这样，模型会根据训练数据来学习特征和目标变量之间的关系，并生成一个拟合的决策树回归模型。
  在训练过程中，模型会根据特征的不同取值进行划分，并计算每个划分节点的最佳划分方式，以最小化目标变量的误差。通过不断迭代和优化，模型将生成一棵拟合训练数据的决策树模型。训练完成后，regressor 对象就包含了训练得到的决策树回归模型，可以用于对新的输入数据进行预测。

预测模型：

dt_y_pred = regressor.predict(X_test)

  regressor.predict(X_test) 调用了决策树回归模型对象 regressor 的 predict() 方法，传入测试数据集 X_test 作为参数。模型会根据学习到的规则和划分准则，对测试数据集进行预测，并返回预测的目标变量值。预测结果会被存储在变量 dt_y_pred 中，每个元素表示对应测试样本的预测值。这样，您可以通过比较预测值和真实值（测试集的目标变量 y_test）来评估模型的性能和准确度。

计算平均绝对误差（MAE）：

mean_absolute_error(y_test, dt_y_pred)

• 运行结果如下：

  在这个结果中，MAE 为 2372.04，这意味着决策树回归模型的平均预测误差约为 2372.04。

计算均方误差（MSE）：

mean_squared_error(y_test, dt_y_pred)

• 运行结果如下：

  在这个结果中，MSE 为 11300579.47，这意味着决策树回归模型的平均预测误差的平方约为 11300579.47。

计算确定系数（$R^2$）：

r2_score(y_test, dt_y_pred)

• 运行结果如下：

  通过计算 R2 分数，可以评估决策树回归模型在测试数据集上的预测能力。R2 分数越接近 1，表示模型的拟合效果越好，能够解释目标变量的方差越多。在这个结果中，R2 分数为 0.552，说明决策树回归模型对目标变量的解释能力一般。

计算均方根误差（RMSE）：

print("RMSE of Linear Regression Model is ",sqrt(mean_squared_error(y_test, dt_y_pred)))

• 运行结果如下：

  RMSE是用于评估回归模型预测性能的指标，它表示预测值与真实值之间差异的平均程度。RMSE的值与被预测的目标变量的单位相同，因此可以直观地了解模型的预测误差大小。在这个结果中，RMSE的值为3361.633452177241，表示决策树回归模型的预测值与真实值之间的平均差异约为3361.633。

21. 构建随机森林回归器（Random Forest Regressor）模型

  随机森林回归器（Random Forest Regressor）是一种集成学习算法，它通过构建多个决策树并综合它们的预测结果来进行回归任务。它结合了决策树的高效性和集成学习的鲁棒性，适用于解决回归问题。
  下面是随机森林回归器的主要步骤：

1. 数据采样：从原始训练数据集中随机有放回地抽取一定数量的样本，形成一个子样本集。这个过程称为自助采样（bootstrap sampling）。
2. 特征随机选择：从所有特征中随机选择一部分特征，一般来说，对于每个决策树而言，特征的选择个数是固定的。
3. 决策树构建：基于子样本集和随机选择的特征，构建一颗决策树。决策树的构建过程中，对于每个节点，选择最佳的切分特征和切分点，使得划分后的子节点中样本的平方误差最小。
4. 构建多个决策树：重复步骤2和3，构建多颗决策树。
5. 预测结果：对于回归任务，将每棵决策树的预测结果综合起来，可以通过简单地取平均值来得到最终的预测结果。

随机森林回归器具有以下特点：

  • 能够处理大量的输入特征，而且在特征数量很大的情况下仍能保持较好的性能。
  • 对于缺失数据的处理具有较好的鲁棒性。
  • 能够有效地处理非线性关系和交互作用。
  • 具有较好的抗过拟合能力，因为每颗决策树都是基于不同的子样本和特征构建的。

  随机森林回归器在实际应用中广泛使用，特别适用于预测问题，如房价预测、销售预测、股票价格预测等。它的集成特性使得模型更加稳健，并且可以通过调整决策树数量和特征选择策略来进行模型优化。

导入了随机森林回归模型：

from sklearn.ensemble import RandomForestRegressor

创建一个随机森林回归器对象：

RFregressor = RandomForestRegressor(random_state = 0)  

训练模型：

RFregressor.fit(X_train, y_train)

  上述代码使用随机森林回归器对象 RFregressor 对训练集数据进行训练。在训练过程中，随机森林回归器会使用多个决策树进行训练，每个决策树使用随机选择的样本和特征子集进行构建。通过对这些决策树的预测结果进行平均或投票，随机森林回归模型能够提供更准确和稳定的预测结果。训练完成后，RFregressor 对象就包含了训练好的随机森林回归模型，可以用于进行预测任务。

预测模型：

rf_y_pred = RFregressor.predict(X_test)

  上述代码使用训练好的随机森林回归器 RFregressor 对测试集数据 X_test 进行预测，并将预测结果存储在变量 rf_y_pred 中。

计算平均绝对误差（MAE）：

mean_absolute_error(y_test, rf_y_pred)

• 运行结果如下：

  在这个结果中，MAE 为 2222.05，这意味着随机森林回归模型的平均预测误差约为 2222.05。

计算均方误差（MSE）：

mean_squared_error(y_test, rf_y_pred)

• 运行结果如下：

  在这个结果中，MSE 为 9310769.87，这意味着随机森林回归模型的平均预测误差的平方约为 9310769.87。

计算确定系数（$R^2$）：

r2_score(y_test, rf_y_pred)

• 运行结果如下：

  该结果表示随机森林回归模型对购买金额的预测与真实值之间的拟合程度为 0.6309821516972987，即模型能够解释目标变量的方差的约 63.1%。这意味着随机森林回归模型对购买金额的变化有一定的解释能力，但仍有一部分方差无法被模型解释。

计算均方根误差（RMSE）：

print("RMSE of Linear Regression Model is ",sqrt(mean_squared_error(y_test, rf_y_pred)))

• 运行结果如下：

  在这个结果中，RMSE的值为3051.35541573242，表示随机森林回归模型的预测值与真实值之间的平均差异约为3051.355。

22. 构建XGBoost回归器模型

  XGBoost（eXtreme Gradient Boosting）是一种强大的机器学习算法，用于解决回归问题。它是一种梯度提升框架，通过集成多个决策树来建立强大的预测模型。
  XGBoost回归器的工作原理如下：

1. 基本模型：XGBoost回归器由多个决策树组成，每个决策树称为"弱学习器"。初始时，将所有样本的预测值设为一个常数，这个常数是所有样本目标值的平均值。然后，通过迭代的方式，每次添加一个新的决策树来改善模型的性能。
2. 损失函数：XGBoost使用梯度提升算法，通过最小化损失函数来训练模型。回归问题中，常用的损失函数是均方误差（Mean Squared Error）。算法通过计算预测值与实际值之间的误差，然后根据这些误差来更新模型，使预测值逐步逼近真实值。
3. 特征分裂：在每次迭代中，XGBoost使用梯度提升算法来确定应该在哪个特征的哪个取值上进行分裂。它通过计算每个特征的增益（Gain），选择增益最大的特征和分裂点。这样可以使模型更好地捕捉特征之间的关系。
4. 正则化：为了避免过拟合，XGBoost引入了正则化项。它使用了L1和L2正则化来约束模型的复杂度，防止过度拟合训练数据。
5. 提升权重：为了进一步优化模型，XGBoost为每个样本分配一个权重，该权重表示模型对该样本的关注程度。在每次迭代中，算法会根据前一轮的预测误差调整样本的权重，使模型更加关注那些预测不准确的样本。

  XGBoost回归器具有以下特点：

1. 高性能：XGBoost使用并行计算和近似算法来提高训练和预测的速度。它在处理大规模数据集时表现出色，并且能够有效地处理高维特征。
2. 鲁棒性：XGBoost对于缺失值和异常值具有一定的鲁棒性，能够处理各种类型的数据。
3. 可解释性：XGBoost回归器可以提供特征重要性排序，帮助理解模型如何做出预测。
4. 灵活性：XGBoost可以通过调整各种参数来优化模型的性能，包括树的数量、深度、学习率等。

导入XGBoost库中的XGBRegressor类：

from xgboost.sklearn import XGBRegressor

创建一个XGBoost回归模型的实例：

xgb_reg = XGBRegressor(learning_rate=1.0, max_depth=6, min_child_weight=40, seed=0)

  这段代码创建了一个XGBoost回归模型的实例。在这个实例化过程中，我们使用了几个参数来配置模型的行为：

• learning_rate：学习率控制每次迭代中模型权重的更新幅度。较低的学习率可以使模型更加稳定，但可能需要更多的迭代次数才能收敛。
• max_depth：决策树的最大深度，它控制每棵树的复杂度。较大的深度可以提供更丰富的模型表示能力，但也容易过拟合。
• min_child_weight：叶子节点的最小样本权重总和。用于控制决策树分裂的过程中是否继续分裂。较大的权重可以防止过拟合。
• seed：随机种子，用于控制模型的随机性，以便使实验结果可重现。

  通过调整这些参数，您可以对模型的复杂度、学习速率和随机性进行调优，以获得更好的性能和泛化能力。

训练模型：

xgb_reg.fit(X_train, y_train)

预测模型：

xgb_y_pred = xgb_reg.predict(X_test)

计算平均绝对误差（MAE）：

mean_absolute_error(y_test, xgb_y_pred)

• 运行结果如下：

  在这个结果中，MAE 为 2144.86，这意味着XGBoost回归模型的平均预测误差约为 2144.86。

计算均方误差（MSE）：

mean_squared_error(y_test, xgb_y_pred)

• 运行结果如下：

  在这个结果中，MSE 为8268802.18，这意味着XGBoost回归模型的平均预测误差的平方约为8268802.18。

计算确定系数（$R^2$）：

r2_score(y_test, xgb_y_pred)

• 运行结果如下：

  该结果表示XGBoost回归模型对购买金额的预测与真实值之间的拟合程度为 0.67227891659979，即模型能够解释目标变量的方差的约 67.2%，表示模型对数据的拟合效果较好。

计算均方根误差（RMSE）：

print("RMSE of Linear Regression Model is ",sqrt(mean_squared_error(y_test, xgb_y_pred)))

• 运行结果如下：

  在这个结果中，RMSE的值为2875.5525007114747，表示XGBoost回归模型的预测值与真实值之间的平均差异约为2875.55。

五、总结

  下面将上面几个模型的评估指标制作成表格，来对比不同模型的性能：

	线性回归	决策树回归	随机森林回归	XGBoost回归	指标说明
平均绝对误差 (MAE)	3532.07	2372.04	2222.05	★ 2144.86	MAE的值越小，表示模型的预测结果与真实值之间的差异越小，预测能力越好
均方误差 (MSE)	21397853.27	11300579.47	9310769.87	★ 8268802.18	MSE的值越小，表示模型的预测结果与真实值之间的差异越小，预测能力越好
确定系数 ($R^2$)	0.152	0.552	0.631	★ 0.672	R²的值越接近1表示模型对数据的拟合效果越好，越接近0表示模型对数据的拟合效果较差
均方根误差 (RMSE)	4625.78	3361.63	3051.36	★ 2875.55	RMSE越小表示模型的预测能力越好，即预测值与真实值之间的差异较小

  通过对比不同模型的效果，可以得出以下结论：

1. 平均绝对误差(MAE)：随机森林回归和XGBoost回归模型的MAE值较小，分别为2222.05和2144.86，表明这两个模型的预测结果与真实值之间的差异较小，预测能力较好。
2. 均方误差(MSE)：XGBoost回归模型的MSE值最小，为8268802.18，说明该模型的预测结果与真实值之间的差异最小，预测能力最好。
3. 确定系数($R^2$)：XGBoost回归模型的确定系数值最高，为0.672，说明该模型对数据的拟合效果较好，能够解释目标变量的方差的67.2%。
4. 均方根误差(RMSE)：XGBoost回归模型的RMSE值最小，为2875.55，表明该模型的预测能力较好，预测值与真实值之间的差异较小。

  综上所述，基于这些评估指标的比较，XGBoost回归模型在这个问题上表现最好，具有最佳的预测能力和拟合效果。注意，最终选择哪个模型还应考虑其他因素，例如模型的复杂度、训练时间和应用场景等。

  以上就是本项目的全部内容，若想学习更多机器学习或数据分析项目，请关注CSDN本人的博客！如果本文章对您有帮助的话，记得点赞、收藏和分享哦！