动态规划的应用(三):字符串相关问题
本文以 LeetCode 题集为例,介绍动态规划算法解决与字符串相关的问题。
其他动态规划的应用实例:
动态规划的应用(一):最短路问题
动态规划的应用(二):cutting stock 问题
动态规划的应用(四):LeetCode 1900. 最佳运动员的比拼回合
动态规划的应用(五):LeetCode 413, 446. 等差数列划分
动态规划的应用(六):矩阵相关问题
1143. Longest Common Subsequence(最长公共子序列)
问题描述
解决思路
参考资料:最长公共子串(Longest Common SubString)
定义二维数组 d p dp dp,其元素 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示字符串 t e x t 2 text2 text2 的前 i i i 个字符组成的子串,与字符串 t e x t 1 text1 text1 的前 j j j 个字符组成的子串的最大子序列长度。
初始化 d p dp dp 的第一行和第一列;
根据动态规划的思路,按行列顺序遍历其余行列的元素,若 t e x t 2 text2 text2 的第 i i i 个字符与 t e x t 1 text1 text1 的第 j j j 个字符相同,元素 d p [ i ] [ j ] dp[i][j] dp[i][j] 更新为 d p [ i − 1 ] [ j − 1 ] + 1 dp[i - 1][j - 1] + 1 dp[i−1][j−1]+1,否则更新为 d p [ i − 1 ] [ j ] dp[i - 1][j] dp[i−1][j] 和 d p [ i ] [ j − 1 ] dp[i][j - 1] dp[i][j−1] 中的最大值。
最终取右下角的元素作为最终结果即可。
代码实现
题解代码
class Solution(object):
def longestCommonSubsequence(self, text1, text2):
"""
:type text1: str
:type text2: str
:rtype: int
"""
dp = [[0 for _ in text1] for _ in text2]
# initial
for j in range(len(text1)):
dp[0][j] = 1 if text2[0] == text1[j] else dp[0][j - 1] if j else 0
for i in range(1, len(text2)):
dp[i][0] = 1 if text2[i] == text1[0] else dp[i - 1][0]
# dp
for i in range(1, len(text2)):
for j in range(1, len(text1)):
dp[i][j] = dp[i - 1][j - 1] + 1 if text2[i] == text1[j] else max(
[dp[i - 1][j], dp[i][j - 1]])
return dp[-1][-1]
本地代码
class Solution(object):
def longestCommonSubsequence(self, text1, text2):
"""
:type text1: str
:type text2: str
:rtype: int
"""
dp = [[0 for _ in text1] for _ in text2]
# initial
for j in range(len(text1)):
dp[0][j] = 1 if text2[0] == text1[j] else dp[0][j - 1] if j else 0
for i in range(1, len(text2)):
dp[i][0] = 1 if text2[i] == text1[0] else dp[i - 1][0]
# dp
for i in range(1, len(text2)):
for j in range(1, len(text1)):
dp[i][j] = dp[i - 1][j - 1] + 1 if text2[i] == text1[j] else max(
[dp[i - 1][j], dp[i][j - 1]])
return dp[-1][-1]
if __name__ == "__main__":
# str1, str2 = "abcde", "ace" # 实例特点:子序列非连续; 答案:3
# str1, str2 = "bsbininm", "jmjkbkjkv" # 实例特点:最长子序列不唯一; 答案:1
# str1, str2 = "abcba", "abcbcba" # 实例特点:相同字符重复匹配; 答案:5
# str1, str2 = "pmjghexybyrgzczy", "hafcdqbgncrcbihkd" # 实例特点:相同字符多次匹配; 答案:4
str1, str2 = "hofubmnylkra", "pqhgxgdofcvmr" # 答案:5
x = Solution().longestCommonSubsequence(text1=str1, text2=str2)
print()
print(x, '\n')
运行效果
97. Interleaving String(交错字符串)
问题描述
解决思路
参考题解:LeetCode 97 精选题解
(感谢答主的精彩讲解~)
题解代码
class Solution(object):
def isInterleave(self, s1, s2, s3):
"""
:type s1: str
:type s2: str
:type s3: str
:rtype: bool
"""
len1 = len(s1)
len2 = len(s2)
len3 = len(s3)
if(len1 + len2 != len3):
return False
dp=[[False] * (len2 + 1) for i in range(len1 + 1)]
dp[0][0]=True
for i in range(1, len1 + 1):
dp[i][0] = (dp[i - 1][0] and s1[i - 1] == s3[i - 1])
for i in range(1, len2 + 1):
dp[0][i] = (dp[0][i - 1] and s2[i - 1] == s3[i - 1])
for i in range(1, len1 + 1):
for j in range(1, len2 + 1):
dp[i][j] = (dp[i][j - 1] and s2[j - 1] == s3[i + j - 1]) or (dp[i - 1][j] and s1[i - 1] == s3[i + j - 1])
return dp[-1][-1]
运行效果
139. Word Break(单词拆分)
问题描述
解决思路与代码实现
关于该问题的思路,很自然的会想到动态规划算法。
笔者的想法是,从头至尾遍历,若字符串前若干字符是字典中的单词,则对字符串后面的片段继续遍历,直到字符串结尾,若最终无剩余片段,则返回 True,否则返回 False。
在具体代码中,笔者采用了对字典中的单词进行遍历的方式,若单词出现在字符串开头,则对后面的片段继续遍历:
class Solution(object):
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: bool
"""
if not s:
return True
for word in wordDict:
if s[: len(word)] == word:
if self.wordBreak(s=s[len(word):], wordDict=wordDict):
return True
return False
但是当提交运行时,发现运行超时,超时的算例为:
s = "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab"
wordDict = ["a", "aa", "aaa", "aaaa", "aaaaa", "aaaaaa", "aaaaaaa", "aaaaaaaa", "aaaaaaaaa", "aaaaaaaaaa"]
该算例的具体问题为,字符串中出现了字典中不存在的字母(字符),于是笔者对原代码做了简单修改:
class Solution(object):
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: bool
"""
# todo: 若字符串中出现了字典中不存在的字母,直接返回 False
set_s = set(s)
set_dict = set(''.join(wordDict))
for c in set_s:
if c not in set_dict:
return False
if not s:
return True
for word in wordDict:
if s[: len(word)] == word:
if self.wordBreak(s=s[len(word):], wordDict=wordDict):
return True
return False
然而事实证明,这种小修小补是不彻底的,再次提交又遇到了超时的算例:
s = "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaabaabaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
wordDict = ["aa", "aaa", "aaaa", "aaaaa", "aaaaaa", "aaaaaaa", "aaaaaaaa", "aaaaaaaaa", "aaaaaaaaaa", "ba"]
肉眼观察,可以看出该算例的结果也是 False,但是具体问题在于,两个 “ba” 字符之间的 “a” 无法由字典中的单词拼接而成。这个问题就很难用边界情况的应对方式进行处理了,笔者一时也想不出合适的修改方案,于是只好去题解中学习……
看到精选题解中的动态规划解法,笔者发现了自己的问题。正确的方式是直接对字符串中的字符进行遍历,而非对字典中的单词遍历,以切分字符串的前后片段;此外,定义一个长度为 n + 1 n + 1 n+1 的数组,以存储各位置的子串(前 i i i 个字符)能否被字典中的单词切分。
参考题解:LeetCode 139 精选题解
具体代码如下:
class Solution(object):
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: bool
"""
n = len(s)
dp = [False for _ in range(n + 1)]
dp[0] = True
for i in range(n):
for j in range(i + 1, n + 1):
if dp[i] and s[i: j] in wordDict:
dp[j] = True
return dp[-1]
运行效果
1278. Palindrome Partitioning III(分割回文串 III)
本题位 LeetCode 分割回文串问题的变体,前两道题分别采用回溯法和动态规划,详见笔者的另一篇博客:
LeetCode 题集:回溯法和递归(二)字符串相关问题
问题描述
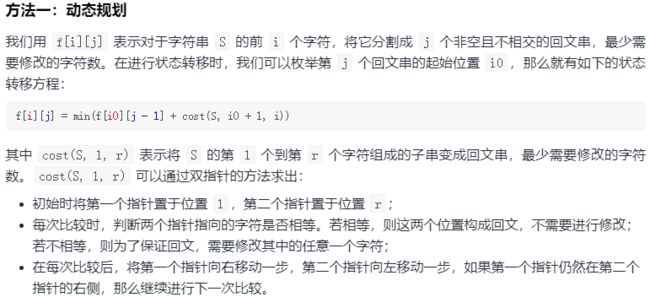
思路与代码
本题不愧是困难级别的题目,看到字符可以修改这个设定,笔者就理不清头绪了,只好去题解中学习,好在官方题解还是很清晰的:
LeetCode 1278 官方题解
class Solution:
def palindromePartition(self, s: str, k: int) -> int:
def cost(left: int, right: int) -> int:
change, i, j = 0, left, right
while i < j:
change += 0 if s[i] == s[j] else 1
i += 1
j -= 1
return change
n = len(s)
dp = [[10 ** 9 for _ in range(k + 1)] for _ in range(n + 1)]
dp[0][0] = 0
for i in range(1, n + 1):
for j in range(1, min(k, i) + 1):
if j == 1:
dp[i][j] = cost(left=0, right=i - 1)
else:
for i0 in range(j - 1, i):
dp[i][j] = min(dp[i][j], dp[i0][j - 1] + cost(i0, i - 1))
return dp[n][k]
代码如下:
class Solution:
def palindromePartition(self, s: str, k: int) -> int:
n = len(s)
cost = [[0 for _ in range(n)] for _ in range(n)]
for span in range(2, n + 1):
for i in range(n - span + 1):
j = i + span -1
cost[i][j] = cost[i + 1][j - 1] + (0 if s[i] == s[j] else 1)
dp = [[10 ** 9 for _ in range(k + 1)] for _ in range(n + 1)]
dp[0][0] = 0
for i in range(1, n + 1):
for j in range(1, min(k, i) + 1):
if j == 1:
dp[i][j] = cost[0][i - 1]
else:
for i0 in range(j - 1, i):
dp[i][j] = min(dp[i][j], dp[i0][j - 1] + cost[i0][i - 1])
return dp[n][k]
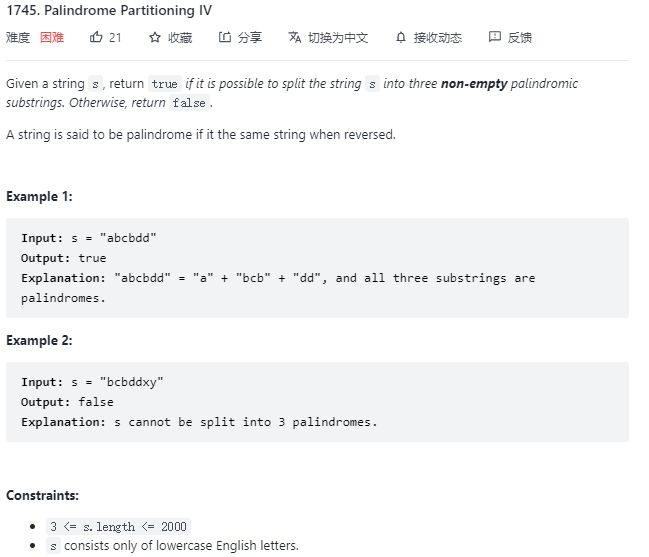
1745. Palindrome Partitioning IV(回文串分割 IV)
问题描述
思路与代码
本题也是分割回文串问题的变体,参考前一题的思路,可以得到基于动态规划的解决方法。
代码如下:
class Solution:
def checkPartitioning(self, s: str) -> bool:
n = len(s)
is_pld = [[True if j == i else False for j in range(n + 1)] for i in range(n + 1)] # index from 1
for span in range(2, n + 1):
for i in range(1, n - span + 2):
j = i + span - 1
if span == 2:
is_pld[i][j] = True if s[i - 1] == s[j - 1] else False
else:
is_pld[i][j] = True if is_pld[i + 1][j - 1] and s[i - 1] == s[j - 1] else False
dp = [[False for _ in range(3 + 1)] for _ in range(n + 1)] # index from 1
dp[1][1], dp[1][2], dp[2][2], dp[3][3] = True, False, True, True
for i in range(1, n + 1):
dp[i][1] = is_pld[1][i] # 1 palindrome
for j in range(2, i + 1): # 2 palindromes
if dp[j - 1][1] and is_pld[j][i]:
dp[i][2] = True
break
for j in range(3, i + 1): # 3 palindromes
if dp[j - 1][2] and is_pld[j][i]:
dp[i][3] = True
if dp[n][3]: # return in advance if found
return True
break
return dp[n][3]
然而,运行效果并不理想,于是笔者到所有提交记录中寻找答案,发现了本题的求解技巧,即由于分割的回文子串数量固定为 3,因此可以采用先掐头去尾、再判断中间字串的方式,简化搜索过程。
代码如下:
class Solution:
def checkPartitioning(self, s: str) -> bool:
# 将字符串分割成 3 个回文字符串,可以就返回 True,否则返回 False
# 注意是得分割成 3 个,单个字符也是回文串
# 分别处理第一个字符和最后一个字符的所有回文串,再判断中间是否有合适的回文串
# 定义辅助函数,判断一个字符串不空,且 s 是回文串
def is_pld(s):
if s and s == s[: : -1]: # s[: : -1] 表示 s 的逆序遍历
return True
else:
return False
# 正序遍历字符串
a_max = [] # 存放前半段找到的回文串的后面元素的下标索引
for i in range(0, len(s)):
# 判断 s 字符串从头开始到 i 结束的片段是否为回文串
if is_pld(s[0: i + 1]):
# 表示在字符串前半段找到了回文串
# 进入循环,表示是回文串,就令 a 数组中加入字符串中该字符下标
a_max.append(i)
# 逆序遍历字符串
b_min = [] # 存放后半段找到的回文串的前面元素的下标索引
for i in range(len(s) - 1, -1, -1):
# 判断字符串 s 从末尾元素开始到前面某位置的片段是否为回文串
if is_pld(s[i: len(s)]):
# 表示在字符串后半段找到了回文串,就在 b 中加入后半段中找到的字符下标
b_min.append(i)
# 前半段和后半段都找完了回文串,且卡住了下标,中间要找的部分就是俩下标中间部分
for a in a_max:
for b in b_min:
# 双重循环遍历中间卡住的片段元素,寻找回文串能不能卡出来
if is_pld(s[a + 1: b]):
return True
return False