LeetCode刷题—动态规划（五）

上一节总结了 0-1背包，接着总结 完全背包。在做题中总结套路，事半功倍！

完全背包

引入
322，零钱兑换，medium
518，零钱兑换Ⅱ，medium
377，组合总和Ⅳ，medium
139，单词拆分，medium
完全背包问题总结

引入

• 完全背包的特点：物品可以无限次选取，且不考虑顺序。

• 与0-1背包不同在：

  • 0-1背包考虑当前物品装入或不装入背包，物品只有一件。

  • 完全背包考虑当前物品装入或不装入背包，物品的数量无限，只要背包容量还有剩余就可以一直拿同一种物品。

• 完全背包的变体问题：物品可以无限次选取，且考虑物品放入的顺序。

下面在具体题目中进行总结。

322，零钱兑换，medium

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

你可以认为每种硬币的数量是无限的。

示例 1：
输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

示例 2：
输入：coins = [2], amount = 3
输出：-1

示例 3：
输入：coins = [1], amount = 0
输出：0

示例 4：
输入：coins = [1], amount = 1
输出：1

示例 5：
输入：coins = [1], amount = 2
输出：2

提示：

1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104

解法一：二维（先遍历物品，再遍历背包）

• 题目解析：

  数组的元素可以使用多次，对顺序没有要求，完全背包问题。

• 思路：

  1. 子问题

     $dp[i][j]$ 前 i 个硬币组成总金额 j，所需最少硬币个数。

  2. base case

     $dp[..][0]=0$ 金额为0，不取硬币。

     特殊情况：

     此题中若无法组成总金额，需返回 -1。思考怎么实现呢？

     把二维数组 $dp$ 初始化成最大值 amount + 1（硬币面额最少为1），如果发现没更新则说明无法取硬币组成总金额，返回 -1。

  3. 递推关系

     最小问题，取min。当前coin = coins[i-1]

     • 不选 coin，最少硬币个数不变，总金额不变。

       $dp[i][j]=dp[i-1][j]$

     • 选 coin，最少硬币个数 + 1。因为完全背包问题可以多次选取同一物品，所以为 $dp[i][j-coin]$，与 0-1背包的区别就体现在此。

       $dp[i][j]=Math.min(dp[i-1][j],dp[i][j-coin]+1)$

• 代码:

  class Solution {
      public int coinChange(int[] coins, int amount) {
          int n = coins.length;
          int[][] dp = new int[n + 1][amount + 1];
          // 初始化dp表，默认值为极大值，代表无解
          for(int i = 0; i < n + 1; i++){
              Arrays.fill(dp[i], amount + 1);
              //base case
              dp[i][0] = 0;
          }
          for(int i = 1; i < n + 1; i++){
              int coin = coins[i - 1];
              for(int j = 1; j < amount + 1; j++){
                  if(j >= coin)
                      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - coin] + 1);
                  else
                       dp[i][j] = dp[i - 1][j];
              }
          }
          return dp[n][amount] > amount ? -1: dp[n][amount];
      }
  }
  

• 状态压缩：

  class Solution {
      public int coinChange(int[] coins, int amount) {
          int n = coins.length;
          int[] dp = new int[amount + 1];
           Arrays.fill(dp, amount + 1);
          //base case
          dp[0] = 0;
          for(int i = 1; i < n + 1; i++){
              int coin = coins[i - 1];
              for(int j = 1; j < amount + 1; j++){
                  if(j >= coin)
                      dp[j] = Math.min(dp[j], dp[j - coin] + 1);
              }
          }
          return dp[amount] > amount ? -1: dp[amount];
      }
  }
  

解法二：一维（先遍历背包，再遍历物品）

• 题目解析：

  数组的元素可以使用多次，对顺序没有要求，完全背包问题。

• 思路：

  1. 子问题

     $dp[i]$ 硬币组成金额为 i ，所需最少硬币个数。

  2. base case

     $dp[0]=0$ 金额为0，不取硬币。

  3. 递推关系

     以 coins=[1,2,5] amount = 11 为例

     k 枚硬币 a1，... ,ak 总和为 11，即 $dp[11]=k$，上一状态就是 $dp[11-ak]=k-1$

     状态转移方程为：

     $dp[i]=min(dp[i-coin])+1$，for coin in coins and if i >= coin

• 代码：

  class Solution {
      public int coinChange(int[] coins, int amount) {
          //特殊判断，可有可无
          if(coins.length == 1 && amount % coins[0] != 0)
              return -1;
                
          int[] dp = new int[amount + 1];
          //硬币面额至少为1，最多为amount
          Arrays.fill(dp, amount + 1);
          dp[0] = 0;
          //外循环为dp数组从1开始的值
          for(int i = 1; i < amount + 1; i++){
              //内循环为 coins 数组元素值
              for(int j = 0; j < coins.length; j++){
                  int coin = coins[j];
                  if(i >= coin)
                      //得到上一状态的最小值
                      dp[i] = Math.min((dp[i - coin] + 1), dp[i]);
              }
          } 
         //如果dp[amount]没更新，返回-1
          return dp[amount] > amount ? -1: dp[amount];
      }
  }
  

518，零钱兑换Ⅱ，medium

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:

输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2:

输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。

示例 3:

输入: amount = 10, coins = [10] 
输出: 1

注意:

你可以假设：

0 <= amount (总金额) <= 5000
1 <= coin (硬币面额) <= 5000
硬币种类不超过 500 种
结果符合 32 位符号整数

• 题目解析：

  数组的元素可以使用多次，对顺序没有要求，完全背包问题。组合问题。

• 思路：

  1. 子问题

     $dp[i][j]$ — 前 i 个硬币组成金额 j 的组合数。

  2. base case

     $dp[..][0]=1$ 全部都不拿，只有这一种拿法。

  3. 递推关系

     $dp[i][j]$ 取决于是否选择 coin = coins[i-1]

     • 如果不选（即不将 coin 装入背包），$dp[i][j]=dp[i-1][j]$
     • 如果选（即将 coin 装入背包），$dp[i][j]=dp[i][j-coin]$，注意此处与 0-1背包 不同，硬币还可再选取。

     要得到总的组合数，状态转移方程为：

     $dp[i][j]=dp[i-1][j]+dp[i][j-coin]$

• 代码：

  class Solution {
      public int change(int amount, int[] coins) {
          int n = coins.length;
          int[][] dp = new int[n + 1][amount + 1];
          for(int i = 0; i < n + 1; i++)
              dp[i][0] = 1;
  
          for(int i = 1; i < n + 1; i++){
              int coin = coins[i - 1];
              for(int j = 1; j < amount + 1; j++){
                  if(j >= coin)
                      dp[i][j] = dp[i - 1][j] + dp[i][j - coin];
                  else 
                      dp[i][j] = dp[i - 1][j];
              }
          }
          return dp[n][amount];
      }
  }
  

• 状态压缩：通过观察可以发现，dp数组的转移只和dp[i][..]和dp[i-1][..]有关，所以可以压缩状态，进一步降低算法的空间复杂度。

  class Solution {
      public int change(int amount, int[] coins) {
  		int n = coins.length;
          int[] dp = new int[amount + 1];
          dp[0] = 1;
          for(int i = 1; i < n + 1; i++){
              int coin = coins[i - 1];
              for(int j = 1; j < amount + 1; j++){
                  if(j >= coin)
                      dp[j] += dp[j - coin];
              }
          }
          return dp[amount];
      }
  }
  

下面两题为完全背包的变体：物品可以无限次选取，且考虑物品放入背包的顺序。

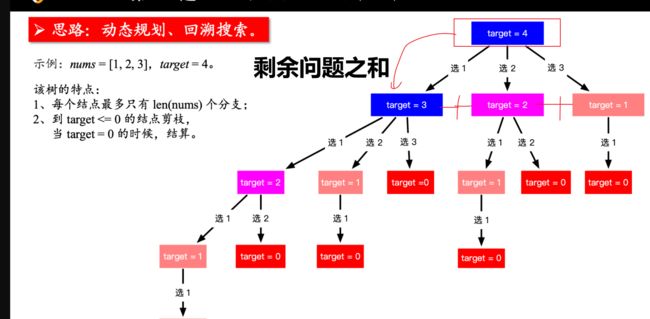
377，组合总和Ⅳ，medium

给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。

示例:

nums = [1, 2, 3]
target = 4

所有可能的组合为：
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

请注意，顺序不同的序列被视作不同的组合。
因此输出为 7。

• 题意分析

  完全背包问题的变体：

  数组的每个元素可以使用多次，直到等于target。

  不同于完全背包：顺序不同的序列被视作不同的组合。

• 思路：

  1. 子问题

     $dp[i]$ —数组的元素组合为 i 的个数。

  2. base case

     $dp[0]=1$ 所有数都不选，只有一种。

  3. 状态转移方程

     

     以 nums =[1,2,3]，target = 4 为例，

     

     即将 target = 4 拆分为 nums[i] 和 dp[target - nums[i]]，最终得到 $dp[4]=dp[3]+dp[2]+dp[1]$

     则状态转移方程为：

     $dp[i]=sum(dp[i-num])$ for num in nums and if i >= num

• 代码：

  class Solution {
      public int combinationSum4(int[] nums, int target) {
          int n = nums.length;
          int[] dp = new int[target + 1];
          dp[0] = 1;
          for(int i = 1; i < target + 1; i++){
              for(int num : nums){
                  if(num <= i){
                      dp[i] += dp[i - num];
                  }
              }
          }
          return dp[target];
      }
  }
  

139，单词拆分，medium

给定一个非空字符串 s 和一个包含非空单词的列表 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1：

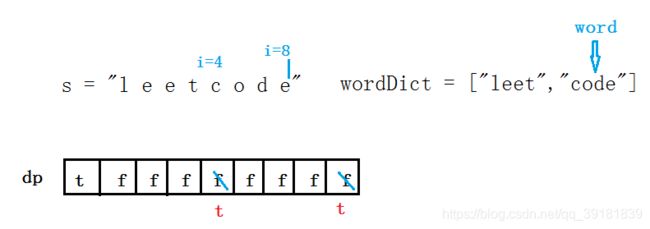
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
     注意你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

• 题意分析

  完全背包问题的变体：物品(wordDict中的单词)可以无限使用，直到填满背包（字符串s）。TRUE / False 问题。

• 思路

  1. 子问题

     $dp[i]$ 字符串前 i 个字符组成的字符串 s[0,i-1] 能否拆分为 wordList 中的单词

  2. base case

     $dp[0]=0$ 表示空串且合法。

  3. 递推关系

     对于物品（wordDict 中的单词），要求有顺序放入背包（字符串s），则将物品迭代置于内循环，将背包迭代放在外循环，这样才能让物品按一定顺序放入背包中。

     如果有单词 等于 字符串s的一部分，需要检查后面的字符串是否能放入背包。

     $dp[i]=dp[i]|dp[i-len];$
     

• 代码：

  class Solution {
      public boolean wordBreak(String s, List<String> wordDict) {
          //s 为背包
          int n = s.length();
          boolean[] dp = new boolean[n + 1];
          dp[0] = true;
  
          for(int i = 1; i < n + 1; i++){
              for(String word : wordDict){
                  int len = word.length();
                  if(i >= len && word.equals(s.substring(i-len, i)))
                      dp[i] = dp[i] | dp[i - len];
              }
          }
          return dp[n];
      }
  }
  

完全背包问题总结

做题步骤：

1. 理解题意，判定此题为 完全背包问题 或 完全背包问题的变体。根据所求分为组合问题，True/False问题，最大最小问题。通常用一维 $dp$ 数组解题。

2. 此题是否有特殊情况

3. 动态规划正常做法

      1. 子问题：确定背包和物品指代什么，$dp[i]$ 返回值是什么
   2. base case：通常为 $dp[0]$
   3. 状态转移方程：
      **先遍历背包，再遍历物品。**这样才能保证放入顺序。
   
   组合问题公式   dp[i] += dp[i - num]
   True/False问题公式    dp[i] = dp[i] or dp[i - num]
   最大最小问题公式    dp[i] = min(dp[i], dp[i - num]+1) 或 dp[i] =  max(dp[i], dp[i - num]+1)
   

4. 最终返回结果