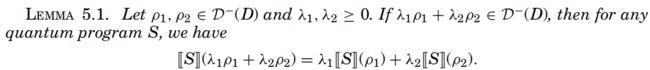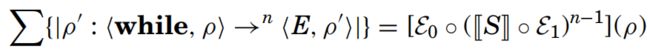量子程序的霍尔逻辑

量子程序的霍尔逻辑

基于应老师的经典论文概述,因本人能力不够不能充分表述，若有错误，敬请指正。且在文中，我将使用简写形式代表数学表示，敬请谅解。

霍尔逻辑是经典程序公理语义的基础。它提供有效的证明技术为推理经典程序的正确性。为提供相似的技术对于量子程序验证并且建立关于量子计算机编程方法的逻辑基础。我们开发了**一个成熟霍尔逻辑用于量子程序的完全和部分正确性。**它证明了这个逻辑是相对完备（是因为其本身建立于哥德尔的不完备性定理基础之上（其本身为基），所以造成其是相对完备）的，通过利用量子程序最弱前置条件（先决）和最弱自由（自由，无约束变量）前置条件的力量（方法）

主题描述：[Programming Languages]形式定义和理论。[Logics and Meanings of Programs]关于程序的指定和验证和推理。规范技术 [Logics and Meanings of Programs]编程语言的语义。操作语义

介绍：人类的直觉更加适合经典世界比起量子世界。qGCL:通过将观察（量子观测）程序作为一种概率选择。 QPL超算子。QML指称语义，在类别理论论述中。状态转换器和谓词转换器建立Stone-type。

提出一种量子系统中信息流的动态逻辑形式，能够描述各种量子操作，如幺正演化和量子测量，特别是在多量子系统中的纠缠。

一个成熟霍尔逻辑对于确定性量子程序，基于超算子，将量子谓词作为厄密特算子，这个逻辑包含了一个关于部分正确性证明系统，一个完全正确性的证明系统对于确定性量子程序。特别的是，我们能够去证明它的（相对）完备性通过利用最弱前置条件和最弱自由前置条件对于量子程序。

3:定义确定性量子程序的语法.

4:一个量子程序的操作语义在量子构建之间的跃迁方面，它包括一个仍要执行的量子程序和一个（部分）密度算子表示程序变量的当前状态。

5：介绍基于操作语义的量子程序标志语义，一个量子程序指称语义被定义为一个从部分密度算子到他自身的函数。

6：采用将量子谓词作为厄密特算子，一个正确性公式定义为一个霍尔三元运算的量子扩展，其包含两个量子谓词，命名为前置条件和后置条件，作为一个量子程序。对于量子程序使用他们的指称语义，引入部分和完全正确性的概念。

7：对于量子程序的最弱前置条件和最弱自由前置条件的全部正确性和部分正确性。

8：一个量子程序的部分正确性证明系统已经被证明，它的（相对）完备性也被证明。

9：在介绍量子环的界函数的概念之后，一个量子程序完全正确性证明系统被给出，它的（相对）完备性也被证明。

10：使用霍尔规则证明Grover的正确性

2》

2.1》》 Hilbert Spaces

我们将C认为为一个复数的集合。

Abelian group需要满足交换律与结合律。
$如果\forall \in >0,存在一个正整数N,使得\left|\left|{\psi }_m-{\psi }_n\right|\right|<\in ,对于m,n\ge N,那么我们将称\left\{|{\psi }_n>\right\}为柯西序列$
在此情况下，I的基数为H的维数。

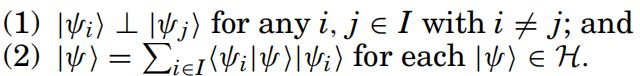
H的正交基，单位向量的{|ψ.i>}

一个希尔伯特空间被认为是一个完整的内积空间，其中每个向量的柯西序列都有一个极限。

根据一个基本的量子力学假设，一个独立的量子系统的状态空间是希尔伯特空间。

系统的纯状态由其状态空间中的一个单位向量来描述。

Example 2.1
(1)量子位为2维希尔伯特空间的状态空间：

在H2中，内积定义为：

显然其都属于C，一个复数集合。

显然{|0>,|1>}为H2的标准正交基，称为计算基。

小知识：

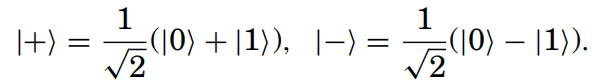
(2) 平方和序列的空间l2为

Z为整数的集合时，H无穷中内积为：

n取负无穷到正无穷之间。显然|n>为正交基在H无穷中

在希尔伯特空间H中的先行操作，映射A:H->H需要满足：

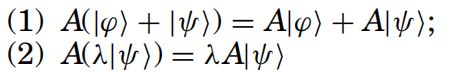
如果{|ψ.i>}是正交基对于H，操作A是仅仅取决于{A|ψ.i>}（在A下的基向量|ψ.i>）
A可以有矩阵表示：

当H是有限维。
我们说A是有界限的在H中，如果 C>=0,例如

在这篇文章中，我们仅考虑有界限算子：
我们写L（H）作为H的有界限算子的集合，在H中的单位算子称为I.H

显然H中的零操作为映射H中的每个向量为零向量记作0.H

对于H中的每一个操作A，存在一个唯一的线性操作A^+在H中

显然当M的共轭矩阵等于M时我们称其为厄密特矩阵，M为H的操作。
显然我们可以得出，当M为正算子时，为厄密特矩阵

如果的可求和对于H中的所有正交基
我们称A为trace class operator(迹类算子) tr(A).

所有我们可以得出，tr显然是依靠于{|ψ.i>}的选择。

将希尔伯特空间H上的密度算子ρ定义为一个具有tr（ρ）=1的正算子。

一个带有状态空间H量子系统的混合状态被H中的密度算子描述。

一个部分密度算子ρ是正算子当tr（ρ）≤1特别的（一个零算子是部分密度算子）

部分密度算子的集合记作
一个部分密度算子也可以被定义为纯态集合。

假设一个量子系统是多纯态|ψ.i>中的一个纯态，各自的概论为p.i

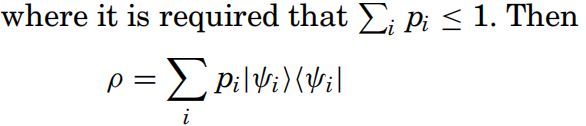
是部分密度算子。部分密度算子的设定允许我们遵循 Selinger的归一化公约。

我们可以在算子中定义一个偏序，称作Lowner 偏序：对于A,B属于L（H）A包含于B如果B-A为正算子。

LEMMA 2.1. A包含于B 当且仅当 tr(Aρ)≤ tr(Bρ)对于所有部分密度算子ρ。

2.2》》酉变换

H中的一个算子U被称为酉变换，如果U的共轭矩阵为它的逆矩阵。

U^+U = I.H ，I.H是密度算子在H。

Example 2.2

(1) 在量子位上最常用的幺正运算是 Hadamard transformation。

Pauli 矩阵：
(2) 设K为整数，k−translation算子在H无穷定义：

很容易辨别U.+k为酉算子。n属于Z

量子力学关于系统演化的基本假设可以表述如下：假设一个闭合的量子系统此时的状态在时刻t0和t是|ψ.0>,|ψ>。它们通过一个酉算子相互关联|ψ>=U|ψ.0>。

等价于 在t时刻一个封闭量子系统状态ρ与在t0时刻状态ρ.0有关，通过幺正算子U

ρ=Uρ.0U^+

2.3》》量子观测

在一个状态空间H的一个量子观测被描述通过，通过收集H上满足归一化条件的算子：

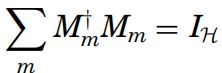
M.m被称为观测算子.m表示实验中可能出现的测量结果。如果量子系统的状态在观测之前是纯状态|ψ>。m所导致的概率为p(m) =
在观测之后系统状态为：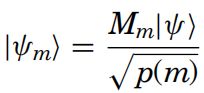
使用密度算子进行量子观测假设，如果量子系统的状态为ρ ，在测量{M.m}之前执行，m所导致的概率p(m) =
在观测之后系统的状态为：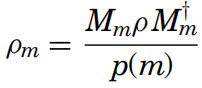
结果：如果测量M只有两个结果0，1,M={M.0,M.1}，称M为yes-no测量。

2.4》》希尔伯特的张量积

复合量子系统的状态空间是其分量的状态空间的张量积。

量子系统变量的类型为布尔和整数，量子系统变量集合为可数无限。

设{|ψ.ij.i>}为H.i的正交基对于每个i，我们写作B 为对于所有H.i的基向量的张量积集合

可知，B 是有限或可数无限集合。我们考虑B是无限的情况：

{H.i}的张量积定义由B张成的希尔伯特空间。

其内积为：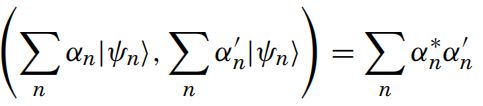
部分迹概念是非常有用的对于描述复合量子系统的子系统。

算子A ∈ L(H ⊗ K)，H,K为两个希尔伯特空间，则在H中的部分迹A为:

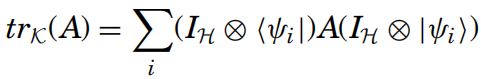
如果H.1和H.2是量子系统q.1和q.2状态，他们的复合系统q.1q.2的状态被密度算子定义ρ ∈ D−(H1 ⊗ H2),tr.H.2(ρ)是对于复合系统q.1状态的描述。

3.》》量子程序的语法

我们假设一个可数无限集合Var对于量子变量

在量子计算机中，一类型应该为量子系统的状态空间定义通过一些量子变量。

类型t是命名为H.t的希尔伯特空间。

我们将注意，布尔和整数类型在经典计算中的集合正是其在量子计算中的基。

变量q的状态空间H.q是通过它的类型在希尔伯特空间定义的。
一个量子寄存器被定义为一个具有不同量子变量的有限序列。

量子寄存器的状态空间-^q = q.1*,…,* q.n是量子变量的状态空间的张量积发生在-^q

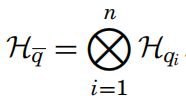
量子程序是量子对于经典while程序的扩展。语法：


定义3.1

集合var(S) 量子变量在量子程序S定义：

4.》》量子程序的操作语义

对于所有量子变量的状态空间的张量积我们写作H.all

使用E来定义空程序。一个量子组态是一对,其中S是一个量子程序或E，ρ ∈D−(H.all)是一个部分密度算子在H.all。它用来预测量子变量全状态。

设-^{q是量子寄存器。一个线性算子A在H.-}q cylinder extension
(1)
其后是密度算子在希尔伯特空间中。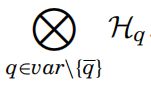
结果：我们可以简单的写出A对于它的拓展Eq.(1)。

量子程序的操作语义被定义作为一个过度关系->在量子组态中

在执行量子程序S之后，一步是在状态ρ，量子变量的状态变成了ρ^’，S’是S的仍待执行的剩余部分。

如果S^{’等价于（量子里面的等价）E，则S终止于状态*ρ*}’.

过度关系->被过度规则所给出在（1）.

图1中的转换规则精确地指定了各种程序构造的含义。

“skip”不需要做任何解释并且立即停止。初始化“q:=0”将量子变量q设置基状态|0>

在规则中（初始化）和队列中，我们使用|ϕ>.q去表明通过量子变量q表示的系统状态|ϕ>。

因此，对于系统q的任意状态|ϕ> , |ψ>，我们可以定义算子|ϕ>.q<ψ|在系统q的状态空间。



|ϕ>.q<ψ|应该理解为它的柱形扩展在H.all根据Eq.（1）。我们可以定义|ϕ>.-^q，|*ϕ*>.-q<ψ|当-^{q是量子寄存器。|*ϕ*>，|*ψ*>在H.-}q中。

注意在此情况下，type(q)=integer,ρ 是一个纯状态，ρ = |ψ>< ψ|,|ψ>∈ H.all

|ψ.k>是一个产品状态对于每一个k：
所以,
在初始化后，状态变成了

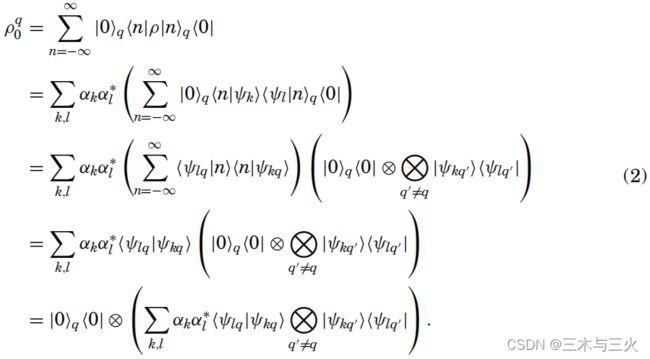
假设ρ通过集合{(p.i**,|ψ*.i>)}纯状态建立。

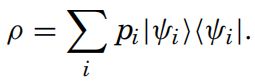
对于每一个i，我们写作ρ.i* = |ψ.i>< ψ.i|,在初始化之后，它变成了ρ.i0^q

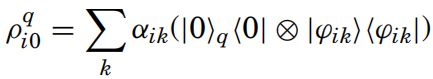
初始化ρ: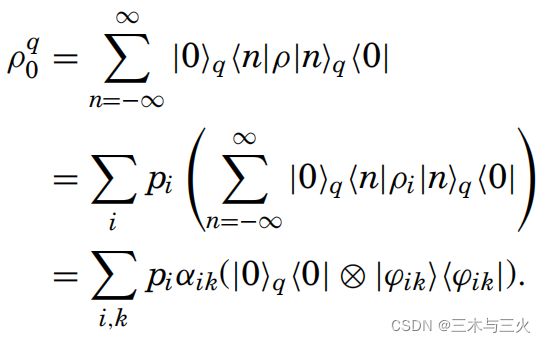

结果m是有概率被观察到的：p.m = tr(M.mρM.m^{+),在测量之后，状态变成ρ.m=M.mρM.m}+/p.m

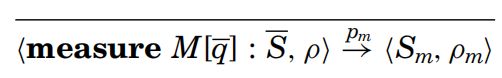
重点是概率发生改变

测量后结果为0，1概率为：


通过n步到达，可以写作：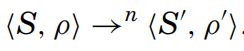
如果其不可拓展，我们就说其开始于ρ，如果其有限，我们说其终止于ρ^’，如果其无限，就说发散。

Example 4.1.
$$xtype(q1)=Boolean，and，type(q2)=integer.$$
$$S\equiv q1:=0;q2:=0;q1:=Hq1;q2:=q2+2;measureM[q1]:\overline{S}$$

5.》》量子程序的指称语义

量子程序的指称语义被定义作为一个映射部分密度算子到自身的语义函数。

对于任意量子程序S，S的语义函数将S的所有终止计算的计算结果相加。

我们为→的自反闭和传递闭包写→*
$<S,\rho >{\to }^{\ast }<S^{‘},{\rho }^{‘}>当且仅当<S,\rho >{\to }^n<S^{‘},{\rho }^{‘}>,n\ge 0$
Defifinition 5.1 设S是一个量子程序。它的语义函数为：
$\Vert S\Vert ：D^{-}(H_{all})\to D^{-}(H_{all})$
被定义$\Vert S\Vert (\rho )={\sum }_{}\{|{\rho }^{‘}:<S,\rho >{\to }^{\ast }<E,{\rho }^{‘}>|\}$
Example 5.1.

假设type(q) = Boolean,程序为：
$S\equiv q:=0;q:=Hq;\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}M[q]:\overline{S}$
M是根据H.2计算基础{|0>,|1>}的观测。
$\overline{S}\equiv S_0,S_1,S_0\equiv q:=Iq,I是量子位的密度算子,S_1\equiv q:={\sigma }_{x}q$

LEMMA 5.1.

PROPOSITION 5.1.

量子环的语义函数的递推表征

COROLLARY 5.1.
$$\Vert while\Vert (\rho )=M_0\rho M_0^{+}+\Vert while\Vert (\Vert S\Vert (M_1\rho M_1^{+}))$$

语义函数并不增加量子变量的密度算符的迹。

PROPOSITION 5.2.
对于任何量子程序S
$$tr(\Vert S\Vert (\rho ))\le tr(\rho )对于所有\rho \in D^{-}(H_{all})$$

PROPOSITION 5.3

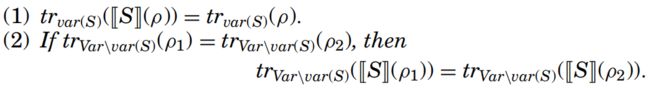
当所有量子变量的全局状态都为ρ时，trX（ρ）描述了非X中的量子变量的状态。

书上很重要！

6.》》正确性公式

量子程序的正确性通过霍尔三元组的量子扩展。一个量子谓词描述程序输入状态，一个量子谓词描述程序输出状态。

$$\begin{gathered} 写P(H_X)作为在H_X上量子谓词的集合，对于\forall \rho \in D^{-}(H_X) \\ tr(P_{\rho })表示谓词P在状态\rho 被满足的概率。 \end{gathered}$$

一个正确性公式是对下列形式的陈述表达：

$$S为量子程序，P,Q为在H_{all}中的量子谓词$$

量子谓词P被称为正确性公示的前置条件，显然Q为后置条件。

一个正确性公式可以用两种不同的方式解释：

Defifinition 6.1.

$$\begin{gathered} （1）正确性公式在完全正确性的意义上是正确的，写作：{\models }_{tot}\left\{P\right\}S\left\{Q\right\} \\ 如果我们有这样的条件： \\ tr(P_{\rho })\le tr(Q\Vert S\Vert (\rho )) \\ 对于\forall \rho \in D^{-}(H) \end{gathered}$$

$$\begin{gathered} （2）正确性公式在部分正确性的意义上是正确的，写作：{\models }_{par}\left\{P\right\}S\left\{Q\right\} \\ 如果我们有这样的条件： \\ tr(P_{\rho })\le tr(Q\Vert S\Vert (\rho ))+[tr(\rho )-tr(\Vert S\Vert (\rho ))] \\ 对于\forall \rho \in D^{-}(H) \end{gathered}$$

显然，我们可以得出，之所以出现完全与部分两种区别，关键点在于S的区别，S若为量子环，
$$tr(\rho )-tr(\Vert S\Vert (\rho ))是程序S从输出状态\rho 发散的概率$$
具体看书。

PROPOSITION 6.1.

7.》》最弱前置条件和最弱自由前置条件

量子程序的最弱前置条件和最弱自由前置条件对建立量子程序弗洛伊德-霍尔逻辑的（相对）完备性方面起着关键作用。

Defifinition 7.1.
$$设S为量子程序且P\in P（H_{all}）为在H_{all}中的量子谓词$$

$$\begin{gathered} 相对于P的S的最弱前置条件被定义为量子谓词wp.S.P\in P(H_{all}) \\ 满足接下来的条件： \\ (1){\models }_{tot}\left\{wp.S.P\right\}S\left\{P\right\}; \\ (2)如果量子谓词Q\in P(H_{all})满足{\models }_{tot}\left\{Q\right\}S\left\{P\right\}，那么Q⊑wp.S.P \end{gathered}$$

$$\begin{gathered} 相对于P的S的最弱自由前置条件被定义为量子谓词wlp.S.P\in P(H_{all}) \\ 满足接下来的条件： \\ (1){\models }_{par}\left\{wlp.S.P\right\}S\left\{P\right\}; \\ (2)如果量子谓词Q\in P(H_{all})满足{\models }_{par}\left\{Q\right\}S\left\{P\right\}，那么Q⊑wlp.S.P \end{gathered}$$

PROPOSITION 7.1.

其中最为重要结论：

PROPOSITION 7.2.

太多了！看书。

其中最为重要结论：

一些额外的：


就是纯上下确界的转换。

下一个命题给出了量子环最弱前置条件和最弱自由前置条件的递归刻画，并为证明量子弗洛伊德-霍尔逻辑的完备性提供了关键步骤。

PROPOSITION 7.3.
$$\begin{gathered} 我们写\mathbf{w}\mathbf{r}\mathbf{i}\mathbf{t}\mathbf{e}对于量子环：“whileM[\overline{q}]=1doS”,对于\forall P\in P(H_{all}) \\ (1)wp.while.P=M_0^{†}P{M}_0+M_1^{†}(wp.S.(wp.while.P))M_1. \\ (2)wlp.while.P=M_0^{†}P{M}_0+M_1^{†}(wlp.S.(wlp.while.P))M_1 \end{gathered}$$

---

8.》》具有部分正确性的证明系统

一个量子程序的部分正确性证明系统已经被证明，它的（相对）完备性也被证明。
介绍了关于量子程序的部分正确性的证明系统qPD。

一个正确性公式的可证明性意味着其在部分正确性意义上的正确性。

THEOREM 8.1可靠性
$$\begin{gathered} 证明系统qPD对量子程序的部分正确性是可靠的； \\ 对于所有的量子程序S和量子谓词P,Q\in P(H_{all}) \\ {⊢}_{qPD}\left\{P\right\}S\left\{Q\right\}implies{\models }_{par}\left\{P\right\}S\left\{Q\right\} \end{gathered}$$

一个在部分正确性意义上的量子程序的真值暗示了它在qPD中的可证明性.

注意只是关注于复数的表示，我们可以将复数字段中正确的所有语句添加到qPD中，以使其完整

THEOREM 8.2完备性
$$\begin{gathered} 证明系统qPD对量子程序的部分正确性是完备的； \\ 对于所有的量子程序S和量子谓词P,Q\in P(H_{all}) \\ {\models }_{par}\left\{P\right\}S\left\{Q\right\}implies{⊢}_{qPD}\left\{P\right\}S\left\{Q\right\} \end{gathered}$$

9.》》具有完全正确性的证明系统

对于完全正确性量子程序的证明系统qTD。qTD与qPD的唯一不同在于其对量子环的推理规则。为了给出量子环的完全正确性的规则，我们需要一个界函数的概念，它表示一个量子环在其计算中的迭代次数。

Defifinition 9.1.
$$\begin{gathered} 设P\in P(H_{all})且∊>0， \\ 一个函数t:D^{-}(H_{all})\to N\cup \left\{\infty \right\}被称作(P,∊)量子环whileM[\overline{q}]=1doS的界函数 \\ 它满足接下来的条件： \\ (1)t(\Vert S\Vert (M_1\rho M_1^{†}))\le t(\rho ); \\ (2)tr(P_{\rho })\ge ∊impliest(\Vert S\Vert (M_1\rho M_1^{†}))<t(\rho ); \\ 对于所有的\rho \in D^{-}(H_{all}),N是非负整数的集合。 \end{gathered}$$

通过将该循环的迭代次数趋于无穷大，为证明证明系统qTD的可靠性和完整性提供了一个关键步骤。

LEMMA 9.1.
$$\begin{gathered} 设P\in P\left(H_{all}\right),接下来的两种陈述是等价的： \\ （1）对于所有的∊>0，存在一个关于量子环“whileM[\overline{q}]=1doS”界函数t_{∊}:(P,∊); \\ （2）li{m}_{n\to \infty }tr(P{(\Vert S\Vert ◦{\xi }_1)}^n(\rho ))=0对于所有的\rho \in D^{-}(H_{all}). \end{gathered}$$

THEOREM 9.1可靠性
$$\begin{gathered} 证明系统qPD对量子程序的安全正确性是可靠的； \\ 对于所有的量子程序S和量子谓词P,Q\in P(H_{all}) \\ {⊢}_{qTD}\left\{P\right\}S\left\{Q\right\}implies{\models }_{tot}\left\{P\right\}S\left\{Q\right\} \end{gathered}$$

一个在部分正确性意义上的量子程序的真值暗示了它在qPD中的可证明性.

注意只是关注于复数的表示，我们可以将复数字段中正确的所有语句添加到qPD中，以使其完整

THEOREM 9.2完备性
$$\begin{gathered} 证明系统qPD对量子程序的完全正确性是完备的； \\ 对于所有的量子程序S和量子谓词P,Q\in P(H_{all}) \\ {\models }_{tot}\left\{P\right\}S\left\{Q\right\}implies{⊢}_{qTD}\left\{P\right\}S\left\{Q\right\} \end{gathered}$$
上述定理仅仅是qTD相对于复数场理论的相对完备性，因为qTD中也采用了（规则阶）。

此外，（规则循环总）中界函数存在的条件甚至包含一个渐近声明，其中∊需要覆盖所有正实数。

10.》》一个示例：GROVER 量子搜索算法的推理

搜索空间有N个元素，（0，1,…,N-1）,假设搜索问题有M个解（1≤ M ≤ N/

2）。假设我们得到一个黑盒，在黑盒中解决问题。

在经典程序中，我们需要O（N/M）时间复杂度。但通过GROVER 量子搜索算法，将时间复杂度变为
$$O(\sqrt{\frac{N}{M}})$$
简化步骤：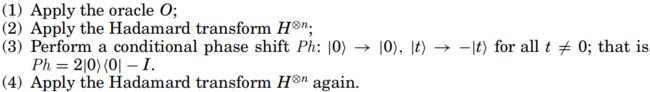
获得高的成功概率：

LEMMA 9.1.