量子计算 2 双缝实验之谜与量子比特
量子计算 2 机率幅和量子比特
- 1 双缝实验之谜?
- 2 机率幅
-
- 2.1 机率幅(Amplitude)
- 2.2 Born rule(2范数很重要)
- 2.3 机率幅表达干涉现象
- 2.4 干涉现象与化学
- 3 量子比特(Qubit)的状态
-
- 3.1 量子比特的纯态(Pure state)
- 3.2 Ket-Bra Notation
- 3.3 Bloch球
- 4 小结和预告
关注我的微信公众号“熙熙学习笔记”可免费阅读全文
今天将从双缝干涉实验的一个奇怪的现象出发,引入描述量子世界的一个重要的数学概念“机率幅/量子幅(Amplitude)”。然后引入我们本系列的重要主角,“量子比特(Qubit)”,描述量子比特的“基态(Basis state)”,和基态的叠加“纯态(Pure state)”,后续推送还会介绍一个纯态的概率分布“混合态(Mixed state)”。
1 双缝实验之谜?
1.1 双缝实验简介
故事一开始,应该是对于光是波还是粒子的讨论,后面科学家做了一个不大一样的实验,不同于之前光束是很多光子组成的,他们一起通过双缝,然后出现干涉现象,科学家们想看看,如果光子一个一个单独通过双缝会有什么现象。最后的结果大家都知道,就是在这种情况下还是出现了干涉条纹,好像是单独的光子自己跟自己发生了干涉,这个就是量子效应的体现。大家还很了解的就是观察会导致干涉条纹消失,即量子效应没有了,退化成了经典世界的现象。在这里经典世界的现象我们不关心,后期推送会讨论观察或者测量的效应,这里我们只讨论一下,在出现量子效应的时候,引起了一个什么问题?
1.2 双缝实验之谜?

图片来自https://www.scottaaronson.com/
单个光子的干涉和单缝实验对比如图所示,我们需要注意的是双缝实验里面,中间有些很暗的地方,我们记为 M i d Mid Mid,说明光子到达这里的概率很低,而单缝实验里面的 M i d Mid Mid位置都是亮的,说明光子到达这里的概率高。重新组织一下语言,会出现下面问题。
P P P记为 事件1:双缝实验中光粒子到达 M i d Mid Mid 的概率;
P 1 P_1 P1记为 事件2:只打开缝隙1时光粒子到达 M i d Mid Mid的概率;
P 2 P_2 P2记为 事件3:只打开缝隙2时光粒子到达 M i d Mid Mid的概率;
我们会自然的认为 P = P 1 + P 2 P=P_1+P_2 P=P1+P2,但是实验结果却表示,可能会出现 P < P 1 + P 2 P
既然用概率 P P P来描述不了,因为概率要大于等于零,那就引进一个可以小于零的量,并将其和概率联系起来,于是机率幅被聪明的科学家们发明了出来。接着往下看。
2 机率幅
机率幅的出现,及其和概率联系起来的方式很简单,但是这种简单的新规则很好的和量子世界的现象对应起来,是很神奇的玩法,不得不说物理学家和数学家们真。
2.1 机率幅(Amplitude)
既然概率要限制在 [ 0 , 1 ] [0,1] [0,1]里面,那我们就定义一个特别自由的机率幅 α ∈ C \alpha \in \mathbb{C} α∈C,即其是一个复数,不仅可以大于零小于零,还能是复数,那就相当自由了。所以我们前面用来描述事件的的概率 P , P 1 , P 2 P, P_1, P_2 P,P1,P2 就用换成用幅值 α , α 1 , α 2 \alpha, \alpha_1, \alpha_2 α,α1,α2。
α \alpha α记为 事件1:双缝实验中光粒子到达 M i d Mid Mid 的机率幅;
α 1 \alpha_1 α1记为 事件2:只打开缝隙1时光粒子到达 M i d Mid Mid的机率幅;
α 2 \alpha_2 α2记为 事件3:只打开缝隙2时光粒子到达 M i d Mid Mid的机率幅;
2.2 Born rule(2范数很重要)
但是呢,我们还是要回归到概率的,于是聪明绝顶的科学家们又发明了一个规则玻恩定理(Born rule),把幅值和概率联系起来。即:
P = ∣ ∣ α ∣ ∣ 2 = Re ( α ) 2 + Im ( α ) 2 P=||\alpha||_2=\text{Re}(\alpha)^2+\text{Im}(\alpha)^2 P=∣∣α∣∣2=Re(α)2+Im(α)2 这个平方用的好用的妙用的呱呱叫,因为有个平方可以解释后面的很多现象,后面还有这个形式的拓展版本,在后续推送里面会进行介绍。
2.3 机率幅表达干涉现象
对应于我们之前认为的 P = P 1 + P 2 P=P_1+P_2 P=P1+P2,现在可以轻松的写成 α = α 1 + α 2 \alpha=\alpha_1+\alpha_2 α=α1+α2。通过玻恩定理可以计算事件1的概率:
P = ∣ ∣ α ∣ ∣ 2 = α α ∗ = α 1 2 + α 2 2 + α 1 α 2 ∗ + α 2 α 1 ∗ P=||\alpha||_2=\alpha\alpha^*=\alpha_1^2+\alpha_2^2+\alpha_1\alpha_2^*+\alpha_2\alpha_1^* P=∣∣α∣∣2=αα∗=α12+α22+α1α2∗+α2α1∗ P 1 = α 1 2 P_1=\alpha_1^2 P1=α12 P 2 = α 2 2 P_2=\alpha_2^2 P2=α22 于是,当 α 1 α 2 ∗ + α 2 α 1 ∗ < 0 \alpha_1\alpha_2^*+\alpha_2\alpha_1^*<0 α1α2∗+α2α1∗<0的时候,比如一个 0.5 0.5 0.5一个 − 0.5 -0.5 −0.5,就很容易得到实验里面的现象: P < P 1 + P 2 P
2.4 干涉现象与化学
可以认为核外电子也处于量子态,它们的幅值由于类似的干涉现象可能会互相抵消,而在幅值不会互相抵消的地方,就形成了离散的能级,这也是化学里面最重要的概念之一。
3 量子比特(Qubit)的状态
好啦,前面的那些东西最后都是为了得到机率幅及其和概率的关系,后面还会再拓展,那就后续推送再说咯。
3.1 量子比特的纯态(Pure state)
量子状态用一个复数空间 C N \mathbb{C}^N CN 单位向量表示。注意状态是可以连续的,但是观察或者测量的结果才是不连续的。
对于一个量子比特来说,其有两种状态,其纯态就是一个二维复数向量来表示,其实就是俩幅值。
3.2 Ket-Bra Notation
为了装逼(不是),我们用Ket Notation来表示这个二维的列向量,用Bra Notation来表示这个二维的行向量(共轭转置)。
Ket Notation表示如下(完蛋CSDN里头的latax不支持ket notation,只能截图了):
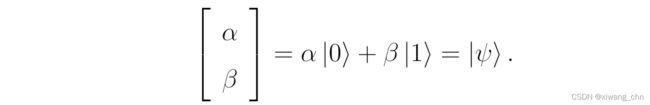
Bra Notation表示如下:
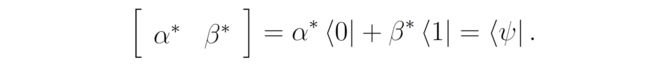
因此| ψ 1 \psi_1 ψ1>和| ψ 2 \psi_2 ψ2>的内积可以表达为< ψ 1 ∣ ψ 2 \psi_1|\psi_2 ψ1∣ψ2>。
其中的|0>和|1>就是基态(Basis state),这里的特殊情况也称为标准基态(standard basis),这个ket notation的好处就是里面是啥都行,比如里面的基态不是0和1,而是一只 |挂掉的> 和 |活着的>,那这两个基态相加,也可以说是量子态叠加(superposition),得到的纯态。那打开箱子就是测量,就牵扯到以后推送的内容啦。
3.3 Bloch球
从Ket Notation再引出俩常用的基态(Hadamard basis):

标准基态和Hadamard basis可以在Block球表示(现在画的是圆,球到后面就需要了)。

4 小结和预告
这次通过双缝干涉实验的讨论引进了机率幅(amplitude),以及定义了量子比特的纯态表达。可以发现现在我们需要的数学也就是线性代数,虽然有点麻烦,但是总可以理解。有了量子比特的表达之后,接下来就要对量子比特进行操作,就像经典比特的操作称为门一样,对量子比特的操作也是门,不过是量子门(quantum gate)。另外,和经典比特不一样的是,观察或者说测量,也算是一种操作。让我们相约下周三,来瞅瞅量子比特的操作是怎么进行的,以及测量有会有什么影响呢?