浅谈数据逻辑结构分类
我们知道,数据是信息的载体,是描述客观事物属性的数、字符及所有能输入到计算机中并被计算机程序识别和处理的符号的集合。
那么,数据元素又是数据的基本单位,通常作为一个整体进行考虑和处理。
由此,数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
一般来讲,数据结构包含三大要素:逻辑结构、存储结构、数据运算。
本文主要围绕数据结构的逻辑进行探讨,其他要素就不一一赘述。
目录
数据逻辑结构的分类
1.线性表
2.栈
3.队列
4.数组
5.串
6.树
7.图
8.堆
数据逻辑结构的分类
常用的数据结构有:线性表,栈,队列,数组,串,树,图,堆八大类,如图所示:
1.线性表
线性表是具有相同数据类型的n个数据元素的有限序列,当n=0时线性表是一个空表
特点:
- 表中元素的个数有限
- 表中元素具有逻辑上的顺序性,表中元素有先后次序
- 表中元素都是数据元素,每个元素都是单个元素
- 每个元素占有相同大小的存储空间
注意:
线性表是一种逻辑结构,表示元素之间一对一的相邻关系
顺序表和链表是指存储结构
如上图,就是线性表数据结构,出第一个元素外,每个元素有且仅有一个直接前驱;除最后一个元素外每个元素有且仅有一个直接后继。
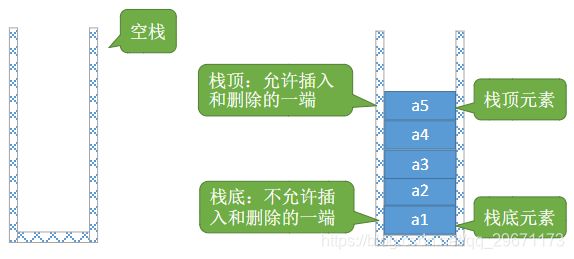
2.栈
栈(Stack)是允许在一段进行插入和删除操作的线性表。
进栈顺序:a1→a2→a3→a4→a5
出栈顺序:a5→a4→a3→a2→a1
特点:后进先出LastInFirstOut(LIFO)或者先进后出。
所以,栈常应用于实现递归功能方面的场景,例如斐波那契数列;栈在现实生活中确实也应用广泛,比如盘子的栈式堆放,羊肉串等。
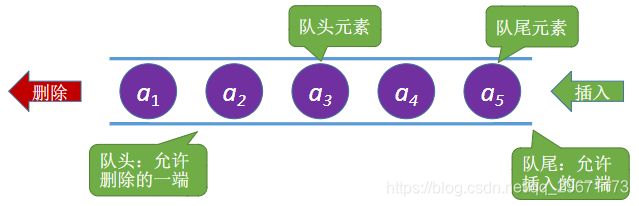
3.队列
队列(Queue)是只允许在一端进行插入,在另一端进行删除的线性表。
特点:先进先出FirstInFirstOut(FIFO)或者后进后出。
所以,队列在多线程阻塞队列管理中非常适用。同时,现实生活中像排队就是队列的经典案例。
4.数组
数组是定长线性表在维数上的扩展,即线性表中的元素又是一个线性表。n维数组是一种”同构“的数据结构,也就是指其每个数据元素类型相同、结构相同。
数组其实就是同一类型的多个变量的集合。
数组元素的特点:
- 数据元素数目固定,一旦定义了一个数组结构,就不再有元素个数的增减变化。
- 数据元素具有相同的类型。
- 数据元素的下标关系具有上下界的约束且下标有序。
数组的基本运算:
- 给定一组下标,存取相应的数据元素。
- 给定一组下标,修改相应的数据元素中某个数据项的值。
5.串
串,即字符串(String)是由零个或多个字符组成的有限序列。一般记为:S= ‘a1a2······an' (n ≥0)
其中,S是串名,单引号括起来的字符序列是串的值;ai可以是字母、数字或其他字符;串中字符的个数n称为串的长度。n= 0时的串称为空串(用∅表示)。
串是一种特殊的线性表,数据元素之间呈线性关系。
串的数据对象限定为字符集(如中文字符、英文字符、数字字符、标点字符等)。
串的基本操作,如增删改查等通常以子串为操作对象。
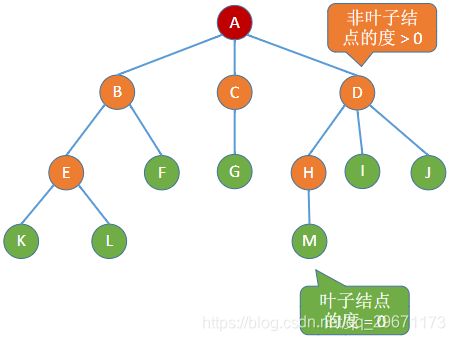
6.树
树是n(n≥0)个结点的有限集合,n= 0时,称为空树,这是一种特殊情况。在任意一棵非空树中应满足:1)有且仅有一个特定的称为根的结点。2)当n> 1时,其余结点可分为m(m> 0)个互不相交的有限集合T1, T2,..., Tm,其中每个集合本身又是一棵树,并且称为根结点的子树。
非空树的特性:
有且仅有一个根结点
- 没有后继的结点称为“叶子结点”(或终端结点)
- 有后继的结点称为“分支结点”(或非终端结点)
- 除了根节点以外,任何一个结点都有且仅有一个前驱
- 每个结点可以有0个或多个后继
简单提下森林,森林是m(m≥0)棵互不相交的树的集合。森林和树可以相互转化。
树有很多种,像平衡二叉树、二叉排序树、哈夫曼树,B树,B+树等。比如哈夫曼树就适用于压缩技术,B+树应用于mysql数据库的索引中。
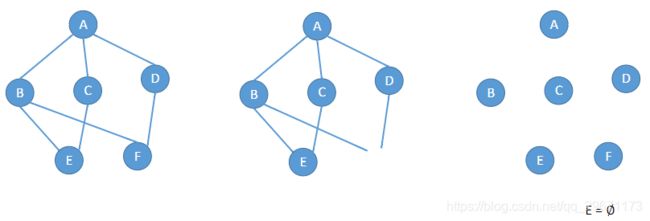
7.图
图G由顶点集V和边集E组成,记为G= (V, E),其中V(G)表示图G中顶点的有限非空集;E(G)表示图G中顶点之间的关系(边)集合。若V= {v1, v2,... , vn},则用|V|表示图G中顶点的个数,也称图G的阶,E= {(u, v) | u∈V, v∈V},用|E|表示图G中边的条数。
注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集。
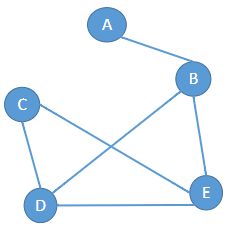
若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的无序对,记为(v, w)或(w, v),因为(v, w) = (w, v),其中v、w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w)依附于顶点w和v,或者说边(v, w)和顶点v、w相关联。
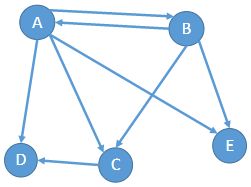
若E是有向边(也称弧)的有限集合时,则图G为有向图。弧是顶点的有序对,记为
图在存储结构上有很多算法,比如有邻接矩阵 、邻接表、十字链表、邻接多重表等。在现实生活中,图应用也很广泛,如联系人之间的好友关系、国内的铁路交通网等。
8.堆
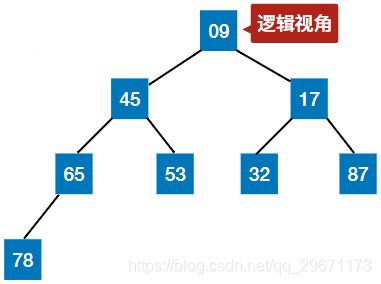
若n个关键字序列L[1...n] 满足下面某一条性质,则称为堆(Heap):
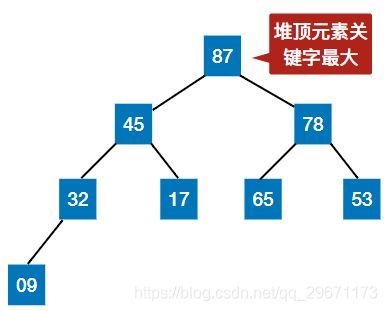
① 若满足:L(i)≥L(2i)且L(i)≥L(2i+1)(1 ≤i ≤n/2)—— 大根堆(大顶堆)
② 若满足:L(i)≤L(2i)且L(i)≤L(2i+1) (1 ≤i ≤n/2)—— 小根堆(小顶堆)
因为堆有序的特点,一般用来做数组中的排序,称为堆排序。