11. 深度学习——强化学习
机器学习面试题汇总与解析——强化学习
本章讲解知识点
-
- 什么是强化学习
-
- 围棋举例
-
- 强化学习的两个特点和一个核心
-
- 最简单的强化学习算法
-
- 一个完整的强化学习问题
-
- 进一步深入强化学习的核心
- 本专栏适合于Python已经入门的学生或人士,有一定的编程基础。
- 本专栏适合于算法工程师、机器学习、图像处理求职的学生或人士。
- 本专栏针对面试题答案进行了优化,尽量做到好记、言简意赅。这才是一份面试题总结的正确打开方式。这样才方便背诵
- 如专栏内容有错漏,欢迎在评论区指出或私聊我更改,一起学习,共同进步。
- 相信大家都有着高尚的灵魂,请尊重我的知识产权,未经允许严禁各类机构和个人转载、传阅本专栏的内容。
-
关于机器学习算法书籍,我强烈推荐一本《百面机器学习算法工程师带你面试》,这个就很类似面经,还有讲解,写得比较好。
-
关于深度学习算法书籍,我强烈推荐一本《解析神经网络——深度学习实践手册》,简称 CNN book,通俗易懂。
1. 什么是强化学习
1.1 基本概念
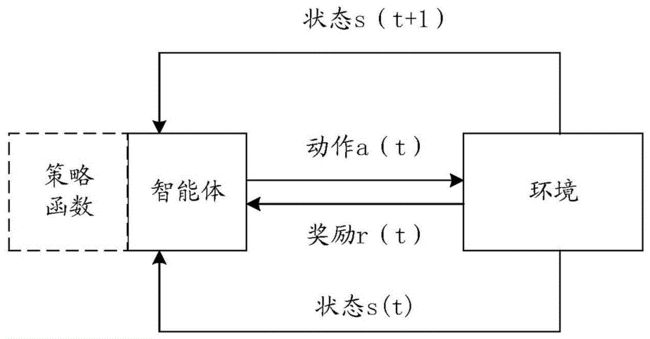
强化学习(Reinforcement Learning)是机器学习的一个分支,通过智能体(Agent)与环境的交互学习最优策略来解决问题。在强化学习中,智能体通过观察环境的状态,采取特定的行动,并从环境中获得奖励或惩罚。智能体的目标是通过与环境的交互,学习出使累计奖励最大化的最优策略。
简而言之,强化学习,是智能体在与环境的互动当中,为了达成一个目标而进行的学习过程。
强化学习在许多领域都有广泛的应用,例如机器人控制、游戏智能、自动驾驶等。它能够在面对复杂、未知或动态的环境中进行决策,并能够通过与环境的交互不断改进策略,具有很强的适应性和灵活性。
1.2 强化学习基本元素(第一层结构)
1.Agent(智能体):
- 智能体是强化学习系统中的决策主体,可以是一个机器学习算法、机器人或其他人工智能实体。
- 智能体通过与环境进行交互来学习和改进自己的策略。
2.Environment(环境):
- 环境是智能体所处的外部世界,可以是真实的物理环境、虚拟环境或模拟器。
- 环境可以对智能体的动作做出响应,提供反馈信息(奖励或惩罚)和更新状态。
3.Goal(目标):
- 目标是强化学习的最终目标或任务,智能体需要通过学习和决策来达到或优化目标。
- 目标可以是预定义的,也可以是根据智能体与环境的交互动态设定的。
1.3 强化学习主要元素(第二层结构)
1.State(状态):
- 状态表示环境在某一时刻的特定情况或特征。如机器人的坐标、敌人的坐标。
- 状态可以是离散的(如迷宫中的位置)或连续的(如机器人的传感器读数)。
2.Action(动作):
- 动作是智能体基于当前状态所选择的行为或决策。
- 动作可以是离散的(如向左或向右移动)或连续的(如机器人的速度控制)。
3.Reward(奖励):
- 奖励是环境提供给智能体的即时反馈,用于评估智能体的行为。
- 奖励可以是正数(奖励)、负数(惩罚)或零(中性)。
1.4 强化学习核心元素(第三层结构)
1.Policy(策略)
在某一个状态下应该采取什么样的行动。简单来说,在数学上,策略就是一个函数,输入当前状态,输出对应动作。很显然,强化学习需要达到的目的就是学习到一个好的策略。
2.Value(价值)
价值同样是一个函数,并且策略函数就取决于价值函数。
价值函数分为两种,一种是状态价值函数,顾名思义,就是输入当前状态,输出状态对应的实数,这个实数就称为对应状态的价值,价值的概念很重要,它指的是预期将来会得到的奖励之和,即处于当前状态下,玩家将来预期得到的所有奖励的一个期望值,玩家的目标就是得到的奖励之和尽可能大,因此通过状态价值函数,玩家应选择进入价值尽可能大的状态,而这是通过特定的行动来实现的,这就是状态价值函数决定了玩家的策略。
另一种价值函数则是状态-行动价值函数,顾名思义,它不单单是指一个状态对应的价值,而是在特定状态下,采取某种行动对应的价值,根据状态-行动价值函数,玩家应该选择价值最大的那一个行动。
1.5 总结
强化学习需要学习的一个东西就是好的价值函数,一个好的价值函数决定了一个好的策略。所有元素之间的关系可以用下图表示:
2. 围棋举例
我们以围棋举例强化学习的过程:
首先第一层结构:
首先 Agent 就是“我”,Environment(环境) 包括了这个棋盘和“我”的对手;Goal(目标) 就是赢得围棋胜利。
然后第二层结构:
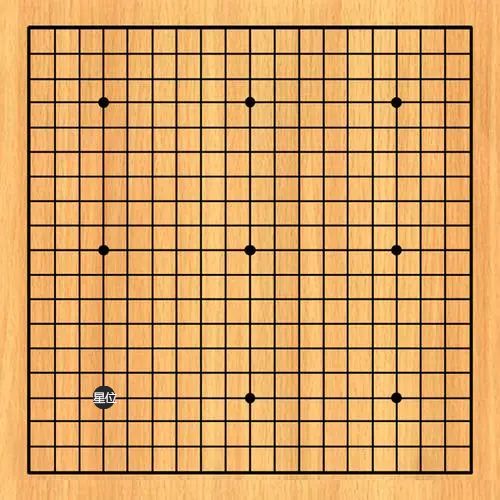
State(状态),在围棋中很简单,也就是棋盘中棋子的分布情况,那么我们目前处于棋盘上没有棋子的状态,我们称之为 State1:
现在假如我执白先行,“我”作为一个玩家,即 Agent,在当前状态下,需要做出某种行动 Action(动作),“我”首先在星位落子,这就是一个行动,我们不妨称之为 Action1:
在“我”采取了该行动之后,我会得到一个即时的反馈,也就是 Reward(奖励) ,对于围棋来说,一个好的强化学习模型,奖励应该是 0,除非达到赢棋的最终状态,所以在这里,Reward1=0。这样就是一个完整的二层结构。
有了行动,对应即时的奖励,同时环境会对这个行动做出响应,比如“我”的对手落子在小目,这就进入了下一个状态 State2,一颗黑棋落在了左下方的星位,一颗白棋落在了右上方的小目。
接下来再进入 Action2、Reward2,再进入 State3,如此下去,直到棋局结束。这就是第二层结构
接下来我们看第三层结构,Policy(策略) 和 Value(价值) 。
我们前面讲了,价值函数分为两种,一种是状态价值函数,另一种价值函数则是状态-行动价值函数,这里我们采取更直接一点的状态-行动价值函数。
让我们回到刚开始的 State1,最为玩家 Agent,“我”在当前状态下应该在哪里落子呢?这就是一个策略问题,在一个状态下采取什么行动,这就是一个 Policy,而策略是由价值决定的,比如,在 State1,我可以落子的位置有 361 种,这 361 种行动对应各自的价值,在一个状态下,可能的行动对应的价值,这就是状态行动价值。
那么这个可能的行动对应的价值是多少呢?我们前面说过价值指的是预期将来会得到的奖励之和的期望值,在围棋中,如果我们规定赢棋的奖励为 1,输棋与和棋的奖励为 0,那么价值实际上就是赢棋的概率,因此,我的策略是选择价值最大,即赢棋概率最大的行动。这就是第三层结构。
这样我们就通过围棋这个例子梳理了强化学习的组成元素以及它们之间的关系。剩下的问题其实就只有一个了,如何学习一个好的价值函数和一个好的策略?这也就是这个强化学习领域最重要的内容。我们会在接下来的内容中详细讲解。而在次,我们还需要了解强化学习的两个特点,和一个核心问题。
3. 强化学习的两个特点和一个核心
3.1 第一个特点
第一个特点叫做 Trial and Error,即试错。强化学习是一种试错学习,也就是在不断的尝试中去学习。现在我们学习围棋,我们会拿着一本棋谱书,这本棋谱书会告诉我们应该在哪里落子,这是一种监督学习,而棋谱告诉我们的其实就是一种策略,这个策略怎么来的?就是古往今来的围棋先辈们通过不断的尝试和不断的对弈总结出来的经验,这就是一种强化学习。在不断下棋的过程中,去学习哪一步棋的价值最大,在不同的情况应该怎么落子,AlphaGo经历的也是同样的过程,这是强化学习的第一大特点,Trial and Error。
3.2 第二个特点
第二个特点则是,Delayed Reward,即延迟奖励。这个特点在围棋中就特别明显,玩家在对弈的过程中,落子得到的奖励都为 0,直到最后获得胜利得到大的奖励,也就是说在下棋过程中,行动没有对应即时的奖励,但是每一步棋对于最后的胜利都是有贡献的,这就导致一个行动可能没有奖励,但是它一定有价值,不过一个行动的价值,只有在得到了奖励后才真正得到体现,而这个奖励可能发生在一段时间之后,在玩家采取了很多其他的行动之后。这就称之为延迟奖励。
在实际得到奖励后,我们知道以前所采取的行动都对这个奖励有贡献,那么如何学习过去的行动所具有的价值,这就涉及到一个 Credit Assignment 和 Backpropagation 的问题,在具体的强化学习算法中我们就可以看到。而在围棋中呢也有同样的过程,我们称之为“复盘”,一局棋结束之后,一方赢,一方输,那么到底哪一步棋起到了关键的作用?哪一步棋的影响不是很大?这时通过“复盘”研究来学习的。实际上,这就是学习每一个动作对应的价值的过程。
3.3 一个核心
在强化学习中,有一个核心问题,就是 Exploration and Exploitation。
Exploitation 就是利用,利用的是强化学习所学到的价值函数,比如我们已经有了一个状态行动价值函数,想当然的应该采取价值最高的行动。但是呢,我们学习到的价值函数不一定是最优的函数,有一些看起来价值不是很高的行动,有可能真实价值是很高的,所以我们不仅仅要利用已有的价值函数,还应该去尝试不同的行动,从而优化我们的价值函数,这就是 Exploitation,即探索。
Exploration and Exploitation 之间的权衡是强化学习中的一个核心问题。在围棋中,就有一个很好的例子,那就是 AlphaGo 的出现给围棋界带来了很多前所未有的新定式,甚至是骚操作。比如开局白棋先行下星位,黑棋小飞挂角,这种情况下,白棋应该怎么应对?通过四千年来的经验总结,定式通常会告诉你,小飞、大飞、单关,压上,或者夹一个都是常见的走法,但是很少会去尖顶,也就是说,人类通过四千多年的学习,认为尖顶这一行动的价值不大,但是我们发现 AlphaGo 常常使用尖顶守角,这也就是说,AlphaGo 通过自己的强化学习,认为这一个行动对应的价值很大,那为什么我们没有发现这一步的价值呢?就是因为我们总是利用已有的价值函数(定式书籍),很少去尖顶,也就是缺乏 Exploitation。
4. 最简单的强化学习算法
4.1. 问题分析
前面我们铺垫了基本知识,剩下的问题其实就只有一个了,如何学习一个好的价值函数和一个好的策略?这也就是这个强化学习领域最重要的内容。
本节我们就要介绍强化学习的具体学习过程,也即算法。我们讲一个最简单的强化学习算法——多臂老虎机。
多臂老虎机是了解强化学习的一个经典问题。老虎机(slot machine)有一个拉杆,每次拉下拉杆,老虎机会随机给出不同数量的硬币。玩家希望尽可能获得多的硬币。怎么获取尽可能多的硬币就是要解决的问题。
强化学习的目标就是学习一个好的策略,做出最优的选择和行动,从而最大化得到的奖励。
我们从强化学习的角度来分析这个问题,Agent 玩家就是“我”,环境 Environment 就是老虎机,现在假设我们有两个老虎机,为什么说这是强化学习中最简单的例子呢?最主要的原因是只有一个状态,老虎机摆在哪里位置不会有任何的改变,这只有一个状态的情况下,玩家只需要在不同的行动中选择一个,即拉动哪一个老虎机的拉杆?另一个原因是没有延迟奖励,因为行动得到的奖励是即时的,拉动老虎机的拉杆就会得到对应奖励,不会对以后的事情产生影响。那么我们只需要学习不同的行动对应的价值即可,即 State-Action Value,状态行动价值,这其中有一个状态,是为了强调行动所具有的价值是和所处的状态有关的,而在老虎机这个问题中,只有一个状态,所以我们可以简化为 Action Value,即行动价值,这个行动价值函数就是最简单的函数了,只有一个输入和输出,输入一个行动,对应输出价值。
我们再来分析下奖励的机制,我选择了一个老虎机后,它随机给了我一个奖励,从本质上来说,我们可以认为这个奖励是一个服从一定概率分布的随机变量,这两个老虎机可能对应的概率分布不一样,但是这两个概率分布是固定不变的,这就是我们所说的状态只有一个。概率分布有一个期望值,那么最优的行动就是选择当时期望值最大的行动,但是玩家并不知道老虎机对应的概率分布是多少,这就是强化学习要做的事情,学习这个概率分布,即学习价值函数。
4.2. 评估老虎机的价值
注意,在真正的现实复杂问题中,应用强化学习是需要去学习价值函数的,即学习价值对应的概率分布,而在老虎机问题中,为了简化问题,我们将直接给出概率分布,即给出了价值函数。但是每一次选择的最大期望价值如何计算呢?
如果有两台老虎机a和b,共给1000次机会,怎么获取更多的硬币呢。
假设已经知道它们给出不同硬币对应的概率如下:
老虎机 a
| 硬币数 | 0 | 1 | 5 | 10 |
|---|---|---|---|---|
| 概率 | 0.7 | 0.15 | 0.12 | 0.03 |
老虎机 b
| 硬币数 | 0 | 1 | 5 | 10 |
|---|---|---|---|---|
| 概率 | 0.5 | 0.4 | 0.09 | 0.01 |
可以计算出老虎机 a 获得硬币的期望值为:
0 ∗ 0.7 + 1 ∗ 0.15 + 5 ∗ 0.12 + 10 ∗ 0.03 = 1.05 0 * 0.7 + 1 * 0.15 + 5 * 0.12 + 10 * 0.03 = 1.05 0∗0.7+1∗0.15+5∗0.12+10∗0.03=1.05
老虎机 b 获得硬币的期望值为:
0 ∗ 0.5 + 1 ∗ 0.4 + 5 ∗ 0.09 + 10 ∗ 0.01 = 0.95 0 * 0.5 + 1 * 0.4 + 5 * 0.09 + 10 * 0.01 = 0.95 0∗0.5+1∗0.4+5∗0.09+10∗0.01=0.95
老虎机 a 的期望高于老虎机 b 的期望,每次选择玩老虎机 a 可以获取更多的硬币。
但是现实中不知道每个老虎机的期望,怎么选择玩哪台呢。概率中以样本均值估计期望值。假设玩某台老虎机 n n n 次,获得硬币数分别为 R 1 , R 2 , . . . R n R_1,R_2,...R_n R1,R2,...Rn ,用 Q n Q_n Qn 表示玩了 n n n 次时对期望的估计值。则:
Q n = R 1 + R 2 + . . . + R n n (.) Q_n = \frac{R_1+R_2+...+R_n}{n} \tag{.} Qn=nR1+R2+...+Rn(.)
根据大数定律,当 n n n 越大,样本均值与期望值越接近。
由公式(1)可以推出以下:
Q n − 1 = R 1 + R 2 + . . . + R n − 1 n − 1 R 1 + R 2 + . . . + R n − 1 = ( n − 1 ) Q n − 1 (.) Q_{n-1} = \frac{R_1+R_2+...+R_{n-1}}{n-1} \\ R_1+R_2+...+R_{n-1}=(n-1)Q_{n-1} \tag{.} Qn−1=n−1R1+R2+...+Rn−1R1+R2+...+Rn−1=(n−1)Qn−1(.)
改写 Q n Q_n Qn 的表示方法:
Q n = R 1 + R 2 + . . . + R n n = 1 n ( R 1 + R 2 + . . . + R n − 1 + R n ) = 1 n ( ( n − 1 ) Q n − 1 + R n ) = Q n − 1 − 1 n Q n − 1 + 1 n R n = Q n − 1 + 1 n ( R n − Q n − 1 ) (.) Q_n = \frac{R_1+R_2+...+R_n}{n} \\ =\frac{1}{n}(R_1+R_2+...+R_{n-1}+R_n) \\ =\frac{1}{n}((n-1)Q_{n-1}+R_n) \\ =Q_{n-1} -\frac{1}{n}Q_{n-1}+\frac{1}{n}R_n \\ =Q_{n-1} + \frac{1}{n}(R_n - Q_{n-1}) \tag{.} Qn=nR1+R2+...+Rn=n1(R1+R2+...+Rn−1+Rn)=n1((n−1)Qn−1+Rn)=Qn−1−n1Qn−1+n1Rn=Qn−1+n1(Rn−Qn−1)(.)
最后有:
Q n = Q n − 1 + 1 n ( R n − Q n − 1 ) (.) Q_n =Q_{n-1} + \frac{1}{n}(R_n - Q_{n-1}) \tag{.} Qn=Qn−1+n1(Rn−Qn−1)(.)
4.3. 策略
假设现在对每个机器都有了期望值的估计,那么可以选择当前估计期望值最大的机器(Exploitation, 利用)。有了价值函数后,我们如何选择行动,当然是选择对应价值最大的那一个行动(贪婪法则)。但是这里会存在一个问题,已知价值函数,那我们每一次岂不是都只玩一个老虎机了?由于实验次数有限,期望的估计值与真实期望值有偏差,当前期望估计值最大的机器可能不是真实期望值最大的机器。如果每次固定选择估计期望值最大的机器,可能难以获取最多的硬币。因此也需要选择那些目前期望估计值不是最大的机器(Exploration, 探索)。什么时候选择目前期望估计值最大的机器,什么时候选择其他机器,这就是权衡利用与探索的问题。做好利用与探索是强化学习的一个关键。
这当然不符合我们的预期,因为我们没有足够探索,已知的价值函数不一定是最优的。这里我们介绍 ϵ \epsilon ϵ-贪婪法则。
ϵ \epsilon ϵ-贪婪法则是一个经典的权衡利用与探索的算法。它以 ϵ \epsilon ϵ 的概率进行探索(Exploration),即随机选择一个老虎机,以 1 − ϵ 1-\epsilon 1−ϵ 的概率进行利用(Exploitation)。
4.4. 实现多臂老虎机算法
简化以上老虎机模型,假设一个老虎机有多个拉杆,每个拉杆被拉下时老虎机以一定概率给出1个硬币或0个硬币。老虎机的建模如下:
import numpy as np
class Bandit:
def __init__(self, arms=10):
self.probs = np.random.rand(arms)
def play(self, arm):
prob = self.probs[arm]
if prob > np.random.rand():
return 1
else:
return 0
以上描述中的玩家在强化学习中一般用术语"代理人"或"智能体"表示,英文为Agent。在这个问题中老虎机就是Agent面临的"环境" (Environment)。强化学习的过程就是Agent采取行动(action)与Environment进行交互,从环境中获取奖励,并且改变环境状态(state)。(目前问题中环境状态不会改变)强化学习的目标是要找到使得获取奖励最大的行动策略(policy)。
在当前问题中以上术语的对应如下:
Agent: 玩家
Environment: 老虎机
action: 拉下拉杆
policy: 怎么选择拉杆
以下实现采用 ϵ \epsilon ϵ-贪婪法则的 Agent:
class Agent:
def __init__(self, epsilon, action_size=10):
self.epsilon = epsilon
self.Qs = np.zeros(action_size) # 记录每个拉杆的期望估计值
self.ns = np.zeros(action_size) # 记录每个拉杆被选择的次数
def update(self, action, reward):
self.ns[action] += 1 # 更新次数
self.Qs[action] += (reward - self.Qs[action]) / self.ns[action] # 更新期望估计, 由公式2计算
def get_action(self):
if self.epsilon > np.random.rand():
return np.random.randint(0, len(self.Qs)) # 以epsilon的概率进行探索,随机选择拉杆
return np.argmax(self.Qs) # 以 1 - epsilon的概率进行利用,选择目前期望估计值最大的拉杆
实际模拟一下以上代理玩老虎机的情形
def play():
steps = 1000
epsilon = 0.1
np.random.seed(123456)
bandit = Bandit()
agent = Agent(epsilon)
total_reward = 0
total_rewards = []
rates = []
for step in range(steps):
action = agent.get_action()
reward = bandit.play(action)
agent.update(action, reward)
total_reward += reward
total_rewards.append(total_reward)
rates.append(total_reward / (step + 1)) # rate表示到目前为止,每一步平均获取的奖励值
print(total_reward)
plt.ylabel("Total reward")
plt.xlabel("Steps")
plt.plot(total_rewards)
plt.show()
plt.ylabel("Rates")
plt.xlabel("Steps")
plt.plot(rates)
plt.show()
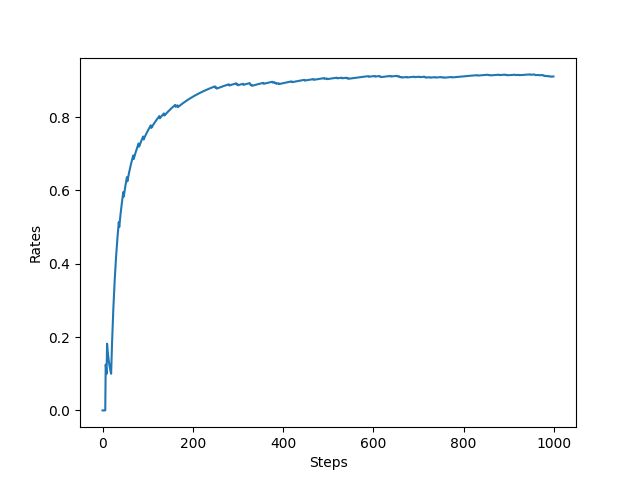
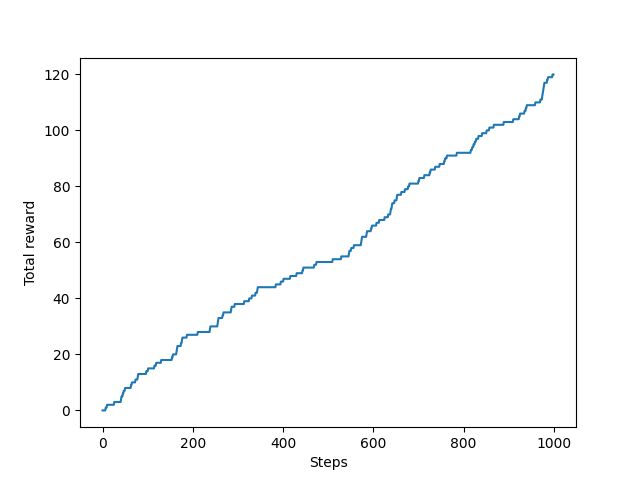
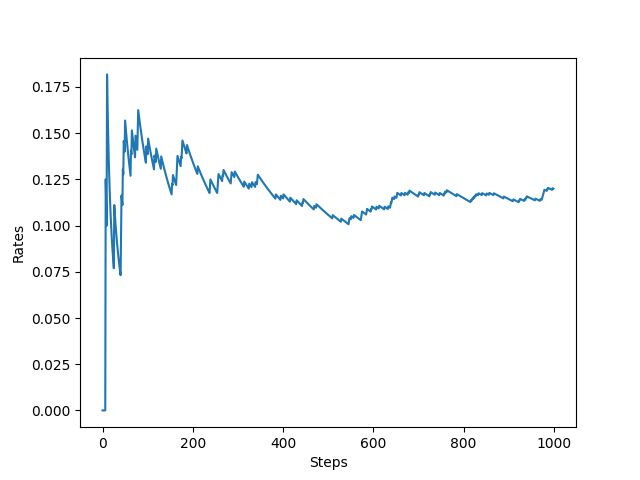
从图中可以看出最终每步平均可以获得大于 0.8 的奖励,表示 ϵ \epsilon ϵ-贪婪法则取得了不错的效果。可以实验一下不进行探索,只利用的策略将会是什么样的结果,将play函数中epislon设置为0,结果如下。可以看出采用只进行利用的策略,无论是奖励总和还是平均奖励与 ϵ \epsilon ϵ-贪婪法则相比都差的比较多。说明了探索的重要性。
5. 一个完整的强化学习问题
这本节中,我们将解决一个有着多种状态和存在延迟奖励的完整的强化学习问题。在这之前我们利用前面讲的价值平均来讲解一个问题,那就是误差 Error。
5.1. 误差 Error
假设 Agent 行动了 n n n 次,每次行动获得的奖励分别为 R 1 , R 2 , . . . R n R_1,R_2,...R_n R1,R2,...Rn ,用 Q n Q_n Qn 表示行动了 n n n 次时对期望价值的估计值。则:
Q n = R 1 + R 2 + . . . + R n n (.) Q_n = \frac{R_1+R_2+...+R_n}{n} \tag{.} Qn=nR1+R2+...+Rn(.)
根据大数定律,当 n n n 越大,样本均值与期望值越接近。
由公式(1)可以推出以下:
Q n − 1 = R 1 + R 2 + . . . + R n − 1 n − 1 R 1 + R 2 + . . . + R n − 1 = ( n − 1 ) Q n − 1 (.) Q_{n-1} = \frac{R_1+R_2+...+R_{n-1}}{n-1} \\ R_1+R_2+...+R_{n-1}=(n-1)Q_{n-1} \tag{.} Qn−1=n−1R1+R2+...+Rn−1R1+R2+...+Rn−1=(n−1)Qn−1(.)
改写 Q n Q_n Qn 的表示方法:
Q n = R 1 + R 2 + . . . + R n n = 1 n ( R 1 + R 2 + . . . + R n − 1 + R n ) = 1 n ( ( n − 1 ) Q n − 1 + R n ) = Q n − 1 − 1 n Q n − 1 + 1 n R n = Q n − 1 + 1 n ( R n − Q n − 1 ) (.) Q_n = \frac{R_1+R_2+...+R_n}{n} \\ =\frac{1}{n}(R_1+R_2+...+R_{n-1}+R_n) \\ =\frac{1}{n}((n-1)Q_{n-1}+R_n) \\ =Q_{n-1} -\frac{1}{n}Q_{n-1}+\frac{1}{n}R_n \\ =Q_{n-1} + \frac{1}{n}(R_n - Q_{n-1}) \tag{.} Qn=nR1+R2+...+Rn=n1(R1+R2+...+Rn−1+Rn)=n1((n−1)Qn−1+Rn)=Qn−1−n1Qn−1+n1Rn=Qn−1+n1(Rn−Qn−1)(.)
最后有:
Q n = Q n − 1 + 1 n ( R n − Q n − 1 ) (.) Q_n =Q_{n-1} + \frac{1}{n}(R_n - Q_{n-1}) \tag{.} Qn=Qn−1+n1(Rn−Qn−1)(.)
即:
Q n + 1 = Q n + 1 n ( R n − Q n ) (.) Q_{n+1} =Q_{n} + \frac{1}{n}(R_n - Q_{n}) \tag{.} Qn+1=Qn+n1(Rn−Qn)(.)
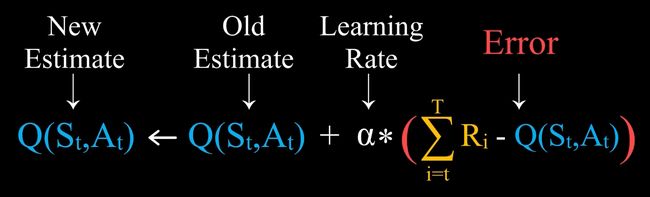
我们得到的这个新公式有什么含义呢? Q n Q_{n} Qn 是在第 n n n 次采取这个行动之前的价值估计, Q n + 1 Q_{n+1} Qn+1 是在第 n n n 次采取这个行动之后的价值估计,我们分别称它们为 Q n Q_{n} Qn:Old Estimate,旧估计, Q n + 1 Q_{n+1} Qn+1:New Estimate,新估计。
为了得到新的价值估计,我们在旧的价值估计的基础上,加上了 1 n ( R n − Q n ) \frac{1}{n}(R_n - Q_{n}) n1(Rn−Qn) 这一项,这一项由一个 1 n \frac{1}{n} n1 和一个差值 ( R n − Q n ) (R_n - Q_{n}) (Rn−Qn) 组成。那么 ( R n − Q n ) (R_n - Q_{n}) (Rn−Qn) 由什么含义呢?价值 Q 的含义是获得奖励的估计值,也就是说,在第 n n n 次采取这个行动之前,我们会得到估计 Q n Q_{n} Qn 的奖励,即 Q n Q_{n} Qn 是我们对于 R n R_n Rn 的一个预测,而第 n n n 次采取这个行动之后,我们实际得到的奖励是 R n R_n Rn,因此 ( R n − Q n ) (R_n - Q_{n}) (Rn−Qn) 是实际值和预测值直接的一个误差!即 Error,我们称之为 Reward Prediction Error,奖励预测误差。 Q n Q_{n} Qn 是对奖励的一个预测, R n R_n Rn 是实际得到的奖励,它们之间的差值也就是奖励预测误差。
存在这样的误差,说明我们的预测并不准确,因此我们需要计算一个新的预测值,这就是 Q n + 1 Q_{n+1} Qn+1, 1 n \frac{1}{n} n1 则是步长,称之为学习率,这样我们就得到了强化学习中一个非常非常重要的原理,那就是基于误差来学习。从而样本平均法这一个看似普通的方法也可以称之为步长为 1 n \frac{1}{n} n1 的误差学习法。步长为 1 n \frac{1}{n} n1 含义就在于随着行动越多,误差对于学习的影响就越来愈小。但是我们希望算法持续学习误差,所以我们不希望步长发生改变,试想一下我们将这个步长变为常数 α \alpha α,
Q n + 1 = Q n + α ( R n − Q n ) (.) Q_{n+1} =Q_{n} + \alpha(R_n - Q_{n}) \tag{.} Qn+1=Qn+α(Rn−Qn)(.)
反向推导后我们又会得到一个新的公式:
Q n + 1 = Q n + α ( R n − Q n ) = ( 1 − α ) n Q 1 + ∑ i = 1 n α ( 1 − α ) n − i R i (.) Q_{n+1} =Q_{n} + \alpha(R_n - Q_{n})\\ =(1-\alpha)^nQ_1 + \sum_{i=1}^n\alpha(1-\alpha)^{n-i}R_i \tag{.} Qn+1=Qn+α(Rn−Qn)=(1−α)nQ1+i=1∑nα(1−α)n−iRi(.)
仔细观察公式,现在的对于价值的估计已经不再是实际得到奖励的平均值了,而是一个加权平均值,并且时间越早得到的奖励权重越小,也就是说,我们更看重最近得到的奖励。显然,这样的算法更加适用于奖励分布可能发生变化的情况。
对比这两个公式后我们发现,算数平均的 Q i Q_i Qi 对后面的价值估计没有影响,但是加强平均的 Q i Q_i Qi 对后面的价值估计有影响。
基于上面的误差概念讲解后,我们就可以运用算法来解决一个完整的强化学习的问题了。
5.2. 完整强化学习问题——OOXX
OOXX 这个游戏大家应该都玩过,英文名叫 tic tac toe。中文也叫井字棋
双方玩家轮流将 X 和 O 放置在一个 3X3 的棋盘上,首先将自己的棋子练成三个的一方获胜。虽然游戏比围棋来说要简单亿点点,但是本质和围棋是一样,都是一个完整的强化学习的过程。存在多种状态,也就是不同状态的棋局,存在延迟奖励,并且行动会对将来的状态变化和得到的奖励产生影响,这里我们就用强化学习来解决井字棋问题。
我们之前讲的数值平均公式,适用于只有一个状态,并且没有延迟奖励的情况。
Q n + 1 = Q n + 1 n ( R n − Q n ) (.) Q_{n+1} =Q_{n} + \frac{1}{n}(R_n - Q_{n}) \tag{.} Qn+1=Qn+n1(Rn−Qn)(.)
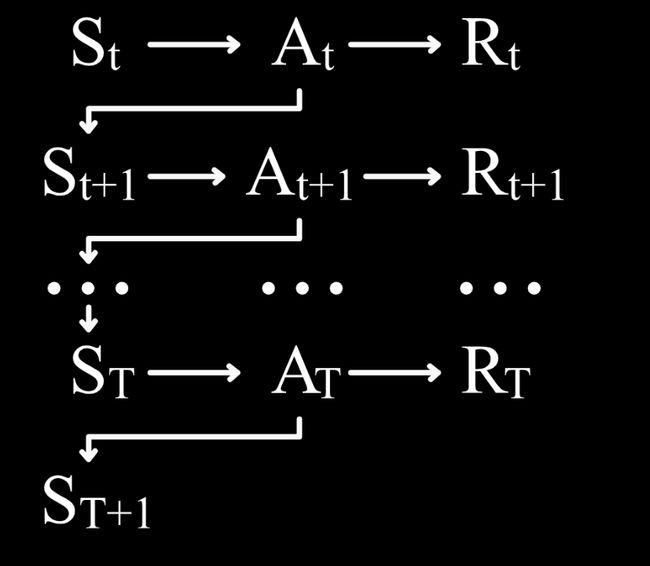
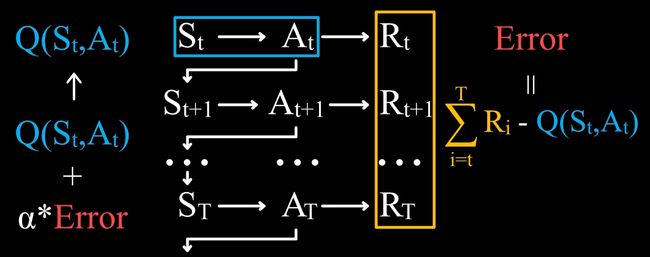
那么如果要解决延迟奖励问题,需要把这个公式推广到状态价值或者状态行动价值。我们假设从 S t S_t St 开始,执行 A t A_t At,得到 R t R_t Rt,然后又从 S t + 1 S_{t+1} St+1 开始,如此循环,直到 S T + 1 S_{T+1} ST+1 时游戏结束。
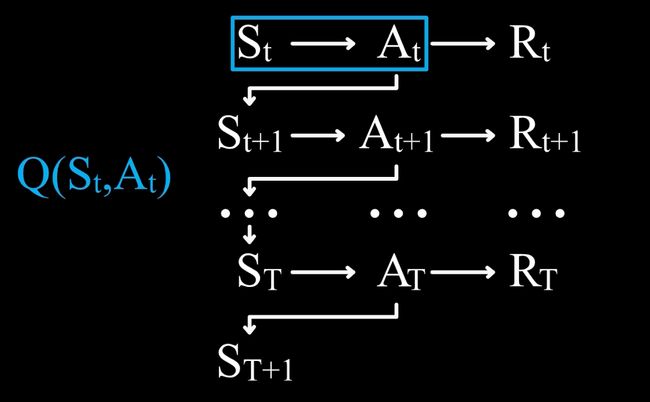
现在如果我们想要学习( S t S_t St, A t A_t At)这一状态行动所具有的价值,应该如何去得到一个基于误差学习的公式呢?
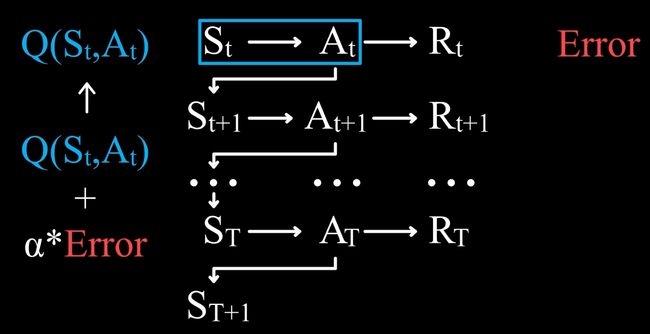
首先我们有一个旧估计 Q( S t S_t St, A t A_t At),那么新估计则应该在旧估计的基础上加上一个学习率 α \alpha α 乘以误差
那么关键问题就来了,什么是误差?我们知道价值的定义是未来所能得到的所有奖励之和的估计值,所以误差应该是实际得到的奖励值和旧估计之间的差值。
因此我们就得到了一个这样的状态行动价值的表达式。
也就是说,在 S t S_t St 状态下,执行 A t A_t At 这一行动后,直到游戏结束,将实际得到的奖励值和旧估计之间的差值,就得到了误差。这便是学习行动状态价值的一种方法,在这个基础上,我们还可以得到另一种方法。注意从 t 时刻开始直到游戏结束所获得的奖励之和,等于 R t R_t Rt 加上从 t+1 时刻开始直到游戏结束所获得的奖励之和,而后面这一项,我们可以用已经有的估计值来替代实际值,也就是 Q( S t + 1 S_{t+1} St+1, A t + 1 A_{t+1} At+1)
这样,我们不需要等到游戏结束就可以计算 Q( S t S_t St, A t A_t At) 的新估计值
其实上面第一行公式这一方法就是蒙特卡洛方法的雏形;而第二行公式就是时序差分法的雏形。它们是以后将会正式讲到的强化学习的核心算法。我们可以从基于误差的学习方法中得到上面两种方法,并且等价的我们可以很容易地写出行动状态价值公式:
有了这些学习公式,再加上 ϵ \epsilon ϵ-贪婪法则,我们就可以解决 OOXX 这个强化学习问题了。
5.3. 代码展示
import numpy as np
class TicTacToeEnvironment:
def __init__(self):
self.board = np.zeros(9)
def reset(self):
self.board = np.zeros(9)
def is_winner(self, player):
win_patterns = [(0, 1, 2), (3, 4, 5), (6, 7, 8),
(0, 3, 6), (1, 4, 7), (2, 5, 8),
(0, 4, 8), (2, 4, 6)]
for pattern in win_patterns:
if all(self.board[i] == player for i in pattern):
return True
return False
def is_draw(self):
return (self.board != 0).all()
def is_game_over(self):
return self.is_winner(1) or self.is_winner(2) or self.is_draw()
def is_valid_move(self, move):
return self.board[move] == 0
def step(self, move, player):
self.board[move] = player
done = self.is_game_over()
return self.board.copy(), done
def get_available_moves(self):
return np.where(self.board == 0)[0]
class QLearningAgent:
def __init__(self, OOXX_index, epsilon=0.1, alpha=0.1, gamma=0.9):
self.value = np.zeros((3, 3, 3, 3, 3, 3, 3, 3, 3))
self.current_state = np.zeros(9)
self.previous_state = np.zeros(9)
self.index = OOXX_index
self.epsilon = epsilon
self.alpha = alpha
self.gamma = gamma
def choose_action(self, state, available_moves):
if np.random.rand() < self.epsilon:
return np.random.choice(available_moves)
else:
q_values = [self.value[tuple(state)][move] for move in available_moves]
return available_moves[np.argmax(q_values)]
def update_value(self, state, action, reward, next_state):
current_q = self.value[tuple(state)][action]
max_next_q = np.max(self.value[tuple(next_state)])
new_q = current_q + self.alpha * (reward + self.gamma * max_next_q - current_q)
self.value[tuple(state)][action] = new_q
def reset(self):
self.current_state = np.zeros(9)
self.previous_state = np.zeros(9)
# 训练参数
num_episodes = 10000
# 创建环境和代理
env = TicTacToeEnvironment()
agent = QLearningAgent(OOXX_index=1)
# 训练循环
for episode in range(num_episodes):
env.reset()
agent.reset()
done = False
while not done:
state = env.board.copy()
available_moves = env.get_available_moves()
# 代理选择动作
action = agent.choose_action(state, available_moves)
# 在环境中执行动作,并获取下一个状态和奖励
next_state, done = env.step(action, player=1)
reward = 1 if env.is_winner(1) else 0
# 更新代理的值函数
agent.update_value(state, action, reward, next_state)
# 训练完成后,你可以使用 agent 的值函数进行预测或者继续训练。
关键部分解读:
- value: 一个 9 维数组,用于存储状态动作值函数 Q。
- currentState: 当前状态。
- previousState: 先前状态。
- index: 玩家标志,1 对应 X,-1 对应 O。
- epsilon: 探索因子,用于平衡探索和利用。
- alpha: 学习率,用于控制 Q 值的更新步长。
方法解读:
-
reset: 重置当前状态和先前状态。
-
choose_action: 根据当前状态选择动作。实现了 ε-greedy 策略,即以 ε 的概率进行随机动作,以 (1-ε) 的概率选择当前 Q 值最大的动作。
-
update_value: 更新 Q 值。使用 Q-learning 的更新规则,通过比较当前状态和先前状态的 Q 值来更新。方法用于更新状态价值表。它使用时序差分学习方法,根据当前状态和先前状态之间的差异来更新状态价值。
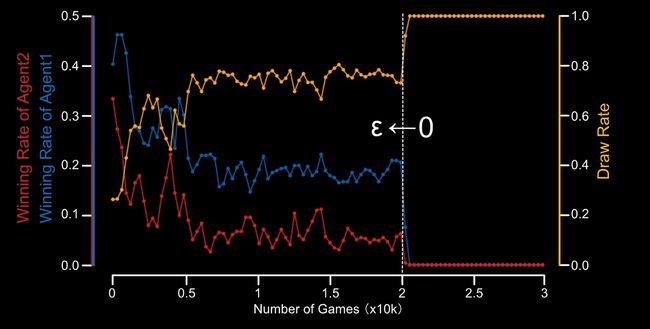
这样我们就编写了一个 OOXX 的强化学习程序,我们创建一个 Agent1 画 O,创建一个 Agent2 画 X,然后让它们对弈三万次,我们让 Agent1 应用强化学习,让 Agent2 随机下棋,这样得到的结果:
可以看到 Agent1 胜率持续上升。而当我们让两个 Agent 都采用强化学习后,就发现和棋的概率上升到了 100%,也就是两个 Agent 都学到了最优策略。
好了,到此为止,我们就讲清楚了强化学习的入门知识,并做出了一定的实践。在后续的内容中,我们将深入强化学习的核心内容。
6. 进一步深入强化学习的核心
以上的内容,我们利用已有的知识解决了一个完整的强化学习问题,但我们还没有深入强化学习的核心算法,接下来我们就一探究竟。关于算法的深入学习,限于篇幅问题,请参考详细教程:https://hrl.boyuai.com/chapter/intro
但是多说几句关于我对核心算法的理解:在深度学习未充分利用的情况下,强化学习始终处于浅智能,马尔可夫算法、动态规划算法、时序差分算法、Q-Leaning算法始终只能解决固定状态、固定场景的问题,如固定目标的循迹,不具备推广的潜质,无法处理状态复杂多变的场景,比如当目标位置发生改变后,就无法再普适处理了。这是因为人工设计的 Q-table 容量有限、维度有限,无法将复杂多变的状态抽象出来并合理存储。但是当深度神经网络出现后,上面困难的解决成为了可能,因为神经网络是个黑盒,中间可以隐含多个神经元,整个神经网络就成了一个 Q-table,于是就可以处理目标位置发生改变的场景了。当强化学习结合深度学习后,人工智能才终于进化到中强智能的程度。
强化学习如何结合深度学习呢?我们之前提到过,强化学习的核心问题是价值函数和策略函数,所以我们以神经网络来替代价值函数和策略函数,最后通过网络的输出来决定 Agent 的 Action,不就实现了结合吗?而且这样做的好处,网络还能自己学习到更优的参数,简直完美。
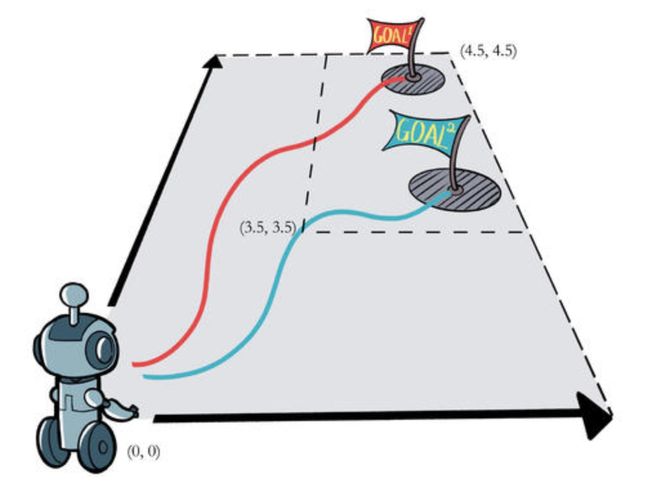
然后我再说一下我实现强化学习过程中的心得,以固定目标循迹为例:
机器人可以上下左右自由移动,它的目标是去寻找地图中的随机位置的 Goal。首先是我们需要将地图状态输入到神经网络中,那么我们要面临的问题就是,怎么描述这个状态?这个不难,我们之前说过,状态就是机器人的位置,目标的位置,甚至障碍的位置,于是这个状态可以是一个二维矩阵,记录了机器人的位置、目标的位置、甚至障碍的位置。不同的物体还要用不同的数字来表示,机器人是0,目标是1,障碍是2。把一个二维矩阵输入进神经网络如何处理应该不用我多说了。
是不是也可以不用输入矩阵,确实可以,甚至只需要输入两组坐标:[[0,0,0],[4,5,1]],前面两个数字代表坐标,第三个数字代表物体类别。有没有注意到,即时其他信息可以摒弃,但是机器人位置和目标位置是不能摒弃的,这就是以目标为导向的强化学习必须做到的,将目标位置信息输入网络,网络才能具体学习到。
接下来就是网络如何价值评估,所以我们要定义规则,当机器人和目标距离缩短,就奖励它,远离就不奖励它,如何衡量距离?是不是就需要输入机器人和目标的坐标信息?
最后就是强化学习中的奖励问题,如何平衡奖励真的是非常难的问题,比如,机器人寻找目标还算简单,靠近就奖励,远离不奖励,如果再加上障碍物的学习,碰撞就惩罚,这时候学习难度倍增,甚至网络压根不收敛,如何平衡奖励与惩罚,真的是需要精心设计奖惩机制。更别说 DeepMind 已实现了星际争霸等多款游戏的强化智能,得多复杂的奖惩机制,可不是跑跑网络练练丹就可以的。
面试题
1. 介绍一下强化学习?⭐⭐⭐
强化学习(Reinforcement Learning, RL)是机器学习的一个分支,其目标是让智能体(agent)通过在环境中的不断交互,学会在特定任务上做出一系列决策,以使得累积的奖励最大化。强化学习的核心特征是学习过程需要通过试错来获取经验,而不是依赖于标记好的训练数据。
强化学习涉及三个主要组成部分:
-
智能体(Agent): 智能体是学习系统,它在执行动作时能够感知环境并做出相应的决策。智能体的目标是通过学习合适的策略来最大化预期的累积奖励。
-
环境(Environment): 环境是智能体所存在的外部系统,它会受到智能体执行动作的影响,并返回相应的状态和奖励。环境的动态性和不确定性是强化学习问题的关键特征。
-
奖励信号(Reward Signal): 奖励信号是环境提供给智能体的反馈,表示智能体在特定状态执行某个动作的好坏。学习的目标就是通过调整策略,使得智能体能够获得更多的累积奖励。
2. 什么是探索与利用的权衡问题?⭐⭐⭐
在强化学习中,探索与利用的权衡是指智能体在学习过程中面临的一个基本问题,即在已知的信息和未知的信息之间进行权衡。这个问题涉及到如何在已经学到的知识中选择最优的行动(利用已知的信息),同时也需要尝试未知的行动以获取更多的信息(探索新的可能性)。
-
利用(Exploitation): 是指智能体根据已有的经验和知识,选择当前认为最好的行动以获取即时的奖励。通过利用,智能体可以在短期内获取相对较好的奖励,因为它基于已知信息作出决策。
-
探索(Exploration): 是指智能体尝试未知的行动,以便发现新的、可能更好的策略。通过探索,智能体有机会发现之前未见过或很少见过的状态和动作组合,从而可能改进其策略并取得更大的长期奖励。